引言
随着大数据时代的到来,我们经常会面临处理高维数据的问题。高维数据不仅增加了计算复杂度,还可能引发“维度灾难”。为了解决这一问题,我们需要对数据进行降维处理,即在不损失太多信息的前提下,将数据从高维空间映射到低维空间。主成分分析(PCA,Principal Component Analysis)就是一种常用的数据降维方法。
简而言之::PCA降维就是把复杂的高维数据简化成更容易理解的低维数据,同时保留最重要的信息,让我们能够更方便地分析和处理这些数据。
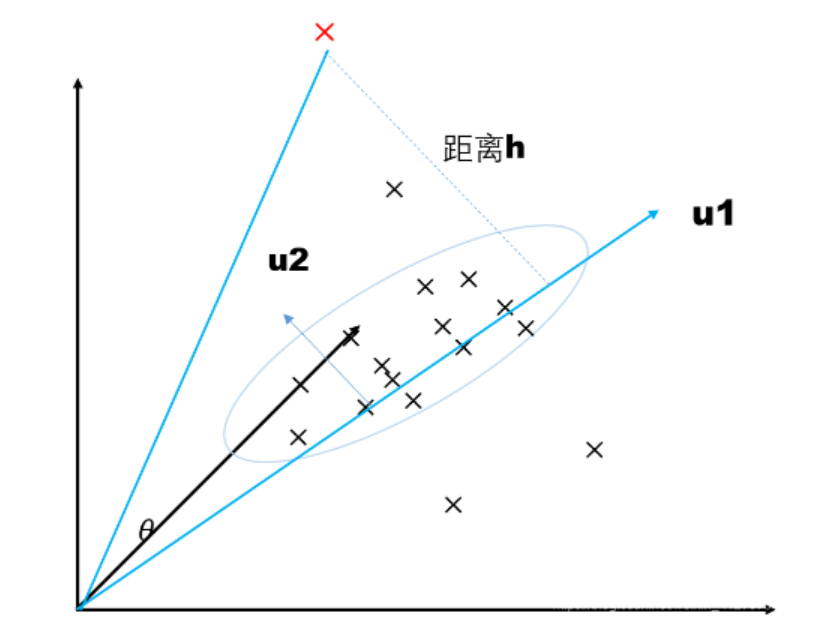
下图为例,所有的数据是分布在三维空间中,PCA将三维数据映射到二维平面u,二维平面由向量<u1,u2>表示,u1与u2垂直
代码演示:
import numpy as np
from sklearn.decomposition import PCA# 创建一个包含五个数据点和两个特征的二维NumPy数组
data = np.array([[1, 1], [1, 3], [2, 3], [4, 4], [2, 4]])# 创建一个PCA对象,通过设置 n_components 参数为 0.9,表示要保留90%的原始数据的方差
pca = PCA(n_components=0.9) # 提取90%特征# 对输入的数据进行PCA模型拟合,计算主成分
pca.fit(data)# 使用拟合好的PCA模型对原始数据进行转换,将数据压缩到新的特征空间,压缩后的结果存储在变量 new 中
new = pca.fit_transform(data) # 压缩后的矩阵# 打印压缩后的数据
print("Compressed Data:")
print(new)# 打印每个选定主成分解释的方差比例。在这里,由于指定了 n_components=0.9,它将打印每个主成分解释的方差比例,直到累积解释的方差达到90%为止
print("Explained Variance Ratios:")
print(pca.explained_variance_ratio_)
压缩后的矩阵:
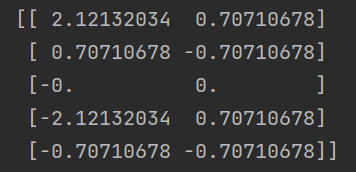
经过PCA降维后的数据。这个矩阵包含了降维后的数据点在新的特征空间中的表示。
简单来说,每一行对应于原始数据中的一个数据点,而每一列对应于新的主成分(新的特征)。在这个例子中,由于设置了 n_components=0.9,只有第一个主成分被保留,因此新的特征空间只有一个维度。
主成分解释的方差比例:
![]()
在提供的数据集 data 中,每个数据点有两个特征。当应用PCA进行降维时,PCA会尝试找到一个新的特征空间,其中第一个主成分(第一个新特征)具有最大的方差,而第二个主成分(第二个新特征)具有次大的方差。详细推导过程可以看我的这篇博客:PCA降维的推导(超详细)_AI_dataloads的博客-CSDN博客
在数据中,PCA计算出的第一个主成分(新特征)具有约0.83的方差,而第二个主成分具有约0.17的方差。因此,第一个主成分保留了数据中大部分的变化和信息,而第二个主成分包含的信息相对较少。因此,降维后,只保留了第一个主成分,而第二个主成分的信息被丢弃了。
这就是为什么降维后只剩下一个主成分,即[0.83333333, 0.16666667]。这意味着降维后的数据集仅包含一个主成分,其中第一个主成分的贡献占主导地位,而第二个主成分的贡献相对较小,因此被删除。这是PCA的工作原理,它试图捕获数据中最重要的变化并减少维度以减小冗余。


![[HXPCTF 2021]includer‘s revenge](https://img-blog.csdnimg.cn/56222c9a8d664c64a10a84c7f50f10bc.png)