暴力解法

创建方法，通过switch-case判断所需要调用的方法。

public class RegionsAndSertches {public static void main(String[] args) {String[] str = new String[]{"NumArray", "sumRange", "update", "sumRange"};int[][] arr = new int[][]{{1, 3, 5}, {0, 2}, {1, 2}, {0, 2}};invoke(str, arr);}public static void invoke(String[] str, int[][] arr) {//str表示上面一行字符串输入，arr表示下面一行二维数组输入NumArray numArray = new NumArray(arr[0]);//第一个必须为NumArray，一定要先创建对象，否则无法调用方法System.out.println("null");//根据题意返回nullfor (int i = 1; i < str.length; i++) {//跳过第一个，索引从1开始//根据输入的字符串判断需要执行哪个方法switch (str[i]) {case "sumRange"://调用sumRange方法，arr[i][0]为left，arr[i][1]为right，方法返回累加和System.out.println(numArray.sumRange(arr[i][0], arr[i][1]));break;case "update"://方法不返回，根据题意输出nullnumArray.update(arr[i][0], arr[i][1]);System.out.println("null");break;default:System.out.println("请输入sumRange或update以执行方法");}}}}class NumArray {public int[] nums;public NumArray(int[] nums) {//构造器this.nums = nums;//创建了哪个对象，this就表示哪个对象}public void update(int index, int val) {this.nums[index] = val;//题目表示nums[index]，不考虑是否加减一}public int sumRange(int left, int right) {int sum = 0;//表示累加和for (int i = left; i <= right; i++) {//left和right都为索引，不用考虑是否加减一sum += this.nums[i];}return sum;}
}

分块处理

其中 n / size 向上取整

 

构造函数

• 计算块大小size=根号n

• 初始化sum块数组

update函数

• 计算新的块数组sum
• 更新nums数组

sumRange函数

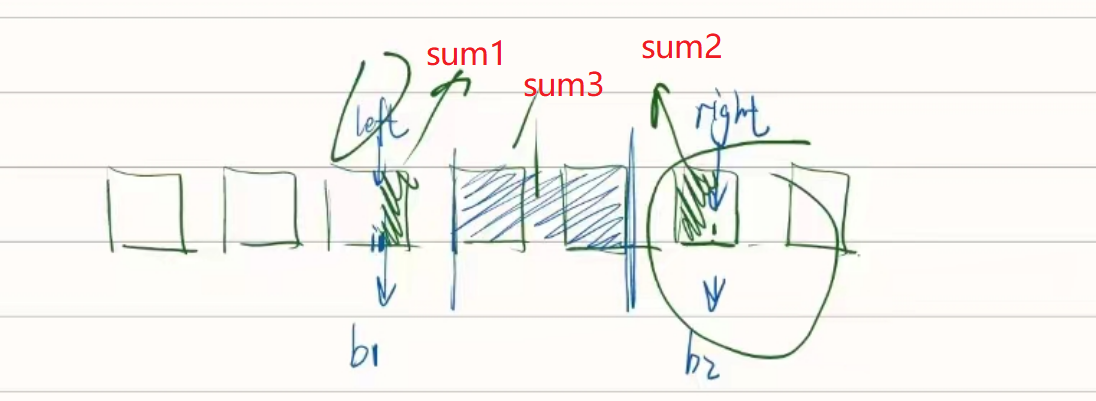
class NumArray {private int[] sum; // sum[i] 表示第 i 个块的元素和private int size; // 块的大小private int[] nums;public NumArray(int[] nums) {this.nums = nums;int n = nums.length;size = (int) Math.sqrt(n);//size的值取根号n，此时的时间复杂度最优sum = new int[n / size + 1];//向上取整for (int i = 0; i < n; i++) {sum[i / size] += nums[i];}}public void update(int index, int val) {// index/size是sum数组的索引sum[index / size] = sum[index / size] - nums[index] + val;//更新sum数组nums[index] = val;//更新nums数组}public int sumRange(int left, int right) {int b1 = left / size, i1 = left % size, b2 = right / size, i2 = right % size;//因为是从b1这块数据内从0开始的索引，需要调整//left - left / size - 1, left=0会越界算出来=-1//避免出现长度为1的数组，一个数被加两次的情况，虽然此时sum3=0，但是sum1和sum2都会加一次if (b1 == b2) { // 区间 [left, right] 在同一块中int sum = 0;for (int j = i1; j <= i2; j++) {sum += nums[b1 * size + j];}return sum;}int sum1 = 0;for (int j = i1; j < size; j++) {//包括leftsum1 += nums[b1 * size + j];}int sum2 = 0;for (int j = 0; j <= i2; j++) {//包括rightsum2 += nums[b2 * size + j];}int sum3 = 0;for (int j = b1 + 1; j < b2; j++) {//b1和b2相等的时候sum3=0,从索引为b1+1的块到b2-1的块之和sum3 += sum[j];}return sum1 + sum2 + sum3;}
}