SARAS多步TD目标算法

代码仓库:https://github.com/daiyizheng/DL/tree/master/09-rl
SARSA算法是on-policy 时序差分

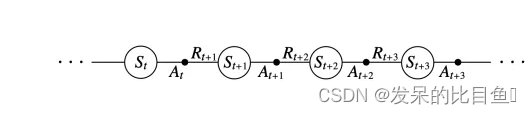
在迭代的时候，我们基于 $ϵ$-贪婪法在当前状态 $S_t$ 选择一个动作 $A_t$ ，然后会进入到下一个状态 $S_{t+1}$ ，同时获得奖励 $R_{t+1}$ ，在新的状态 $S_{t+1}$ 我们同样基于 $ϵ$-贪婪法选择一个动作 $A_{t+1}$ ，然后用它来更新我们的价值函数，更新公式如下:
$Q\left(S_t,A_t\right)\leftarrow Q\left(S_t,A_t\right)+\alpha \left[R_{t+1}+\gamma Q\left(S_{t+1},A_{t+1}\right)-Q\left(S_t,A_t\right)\right]$

• 注意: 这里我们选择的动作 $A_{t+1}$ ，就是下一步要执行的动作，这点是和Q-Learning算法的最大不同
• 这里的 TD Target: ${\delta }_t=R_{t+1}+\gamma Q\left(S_{t+1},A_{t+1}\right)$
• 在每一个非终止状态 $S_t$
• 进行一次更新，我们要获取 5 个数据， $<S_t,A_t,R_{t+1},S_{t+1},A_{t+1}>$

那么n-step Sarsa如何计算

$Q\left(S_t,A_t\right)\leftarrow Q\left(S_t,A_t\right)+\alpha \left(q_t^{(n)}-Q\left(S_t,A_t\right)\right)$

其中 $q_{(n)}$ 为:
$$q_t^{(n)}=R_{t+1}+\gamma R_{t+2}+\cdots +{\gamma }^{n-1}{R}_{t+n}+{\gamma }^{n}Q\left(S_{t+n},A_{t+n}\right)$$

代码

1. 构建环境

import gym#定义环境
class MyWrapper(gym.Wrapper):def __init__(self):#is_slippery控制会不会滑env = gym.make('FrozenLake-v1',render_mode='rgb_array',is_slippery=False)super().__init__(env)self.env = envdef reset(self):state, _ = self.env.reset()return statedef step(self, action):state, reward, terminated, truncated, info = self.env.step(action)over = terminated or truncated#走一步扣一份,逼迫机器人尽快结束游戏if not over:reward = -1#掉坑扣100分if over and reward == 0:reward = -100return state, reward, over#打印游戏图像def show(self):from matplotlib import pyplot as pltplt.figure(figsize=(3, 3))plt.imshow(self.env.render())plt.show()env = MyWrapper()env.reset()env.show()

2. 构建Q表

import numpy as np#初始化Q表,定义了每个状态下每个动作的价值
Q = np.zeros((16, 4))Q

3. 构建数据

from IPython import display
import random#玩一局游戏并记录数据
def play(show=False):state = []action = []reward = []next_state = []over = []s = env.reset()o = Falsewhile not o:a = Q[s].argmax()if random.random() < 0.1:a = env.action_space.sample()ns, r, o = env.step(a)state.append(s)action.append(a)reward.append(r)next_state.append(ns)over.append(o)s = nsif show:display.clear_output(wait=True)env.show()return state, action, reward, next_state, over, sum(reward)play()[-1]

4. 训练

#训练
def train():#训练N局for epoch in range(50000):#玩一局游戏,得到数据state, action, reward, next_state, over, _ = play()for i in range(len(state)):#计算valuevalue = Q[state[i], action[i]]#计算target#累加未来N步的reward,越远的折扣越大#这里是在使用蒙特卡洛方法估计targetreward_s = 0for j in range(i, min(len(state), i + 5)):reward_s += reward[j] * 0.9**(j - i)#计算最后一步的value,这是target的一部分,按距离给折扣target = Q[next_state[j]].max() * 0.9**(j - i + 1)#如果最后一步已经结束,则不需要考虑状态价值#最后累加reward就是targettarget = target + reward_s#更新Q表Q[state[i], action[i]] += (target - value) * 0.05if epoch % 5000 == 0:test_result = sum([play()[-1] for _ in range(20)]) / 20print(epoch, test_result)train()