1. 题目链接:980. 不同路径 III
2. 题目描述:
在二维网格
grid上,有 4 种类型的方格:
1表示起始方格。且只有一个起始方格。2表示结束方格,且只有一个结束方格。0表示我们可以走过的空方格。-1表示我们无法跨越的障碍。返回在四个方向(上、下、左、右)上行走时,从起始方格到结束方格的不同路径的数目**。**
每一个无障碍方格都要通过一次,但是一条路径中不能重复通过同一个方格。
示例 1:
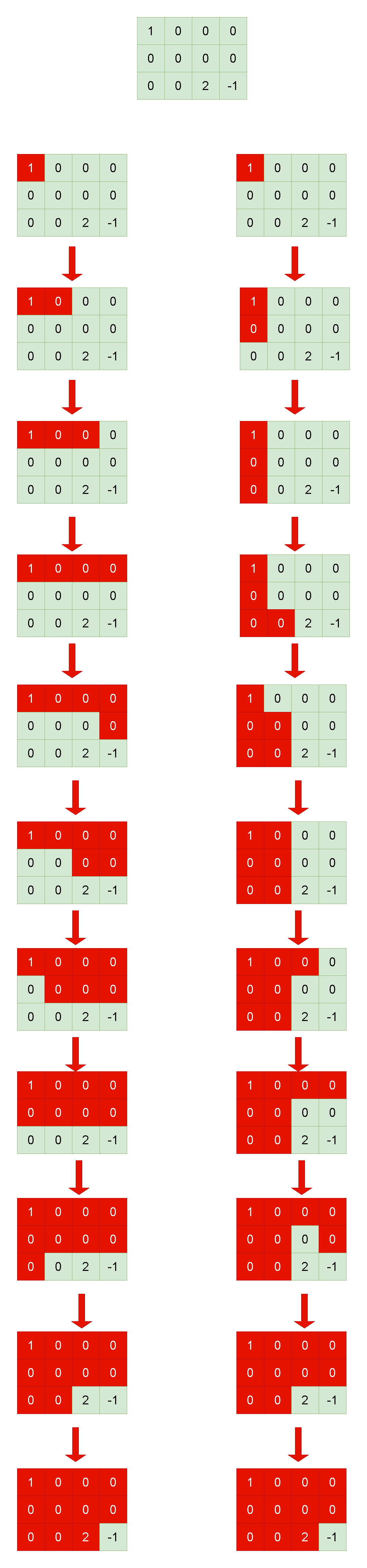
输入:[[1,0,0,0],[0,0,0,0],[0,0,2,-1]] 输出:2 解释:我们有以下两条路径: 1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2) 2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)示例 2:
输入:[[1,0,0,0],[0,0,0,0],[0,0,0,2]] 输出:4 解释:我们有以下四条路径: 1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3) 2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3) 3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3) 4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)示例 3:
输入:[[0,1],[2,0]] 输出:0 解释: 没有一条路能完全穿过每一个空的方格一次。 请注意,起始和结束方格可以位于网格中的任意位置。提示:
1 <= grid.length * grid[0].length <= 20
3. 解法(递归):
3.1 算法思路:
对于四个方向,我们可以定义一个二维数组next,大小为4,每一维存储四个方向的坐标偏移量。题目要求到达目标位置时所有无障碍方块都存在路径中,我们可以定义一个变量记录num当前状态中剩余的未走过的无障碍方格个数,则当我们走到目标地点时只需要判断num是否为0即可,在移动时判断是否越界。
3.2 递归流程:
- 递归结束条件:当前位置的元素为2,若此时可走的位置数量
num的值为0,则cnt的值加一; - 遍历四个方向,若移动后未越界,无障碍并且未被标记,则标记当前位置,并递归移动后的位置,在回溯时撤销标记操作
3.3 C++算法代码:
class Solution {bool vis[21][21]; // 访问标记数组int dx[4] = {1, -1, 0, 0}; // 四个方向的横坐标偏移量int dy[4] = {0, 0, 1, -1}; // 四个方向的纵坐标偏移量int ret; // 结果计数器int m, n, step; // 网格的行数、列数和步数
public:// 计算从起点到终点的唯一路径数量int uniquePathsIII(vector<vector<int>>& grid) {m = grid.size(), n = grid[0].size(); // 获取网格的行数和列数int bx = 0, by = 0; // 起点坐标for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (grid[i][j] == 0) step++; // 统计可走的步数else if (grid[i][j] == 1) {bx = i; // 记录起点坐标by = j;}}}step += 2; // 加上起点和终点的步数vis[bx][by] = true; // 标记起点为已访问dfs(grid, bx, by, 1); // 从起点开始深度优先搜索return ret; // 返回结果计数器的值}void dfs(vector<vector<int>>& grid, int i, int j, int count) {if (grid[i][j] == 2) { // 如果当前位置是终点if (count == step) // 如果已经走过的步数等于总步数ret++; // 结果计数器加一return; // 结束当前递归}for (int k = 0; k < 4; k++) { // 遍历四个方向int x = i + dx[k], y = j + dy[k]; // 计算下一个位置的坐标if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && grid[x][y] != -1) { // 如果下一个位置在网格内且未被访问过且不是障碍物vis[x][y] = true; // 标记下一个位置为已访问dfs(grid, x, y, count + 1); // 继续深度优先搜索vis[x][y] = false; // 回溯,将下一个位置标记为未访问}}}
};