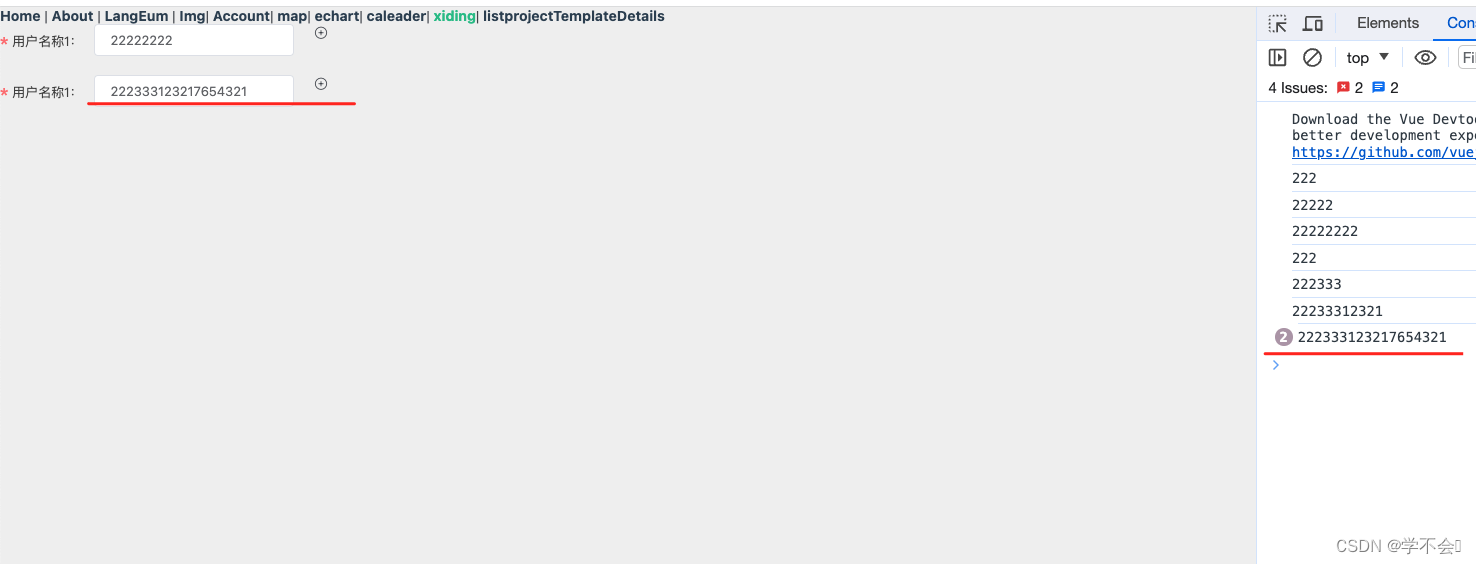
目录
欧拉回路基础
欧拉回路的定义
欧拉回路的性质
判断图中是否存在欧拉回路的java代码实现
寻找欧拉回路的三个算法
Hierholzer算法
详细思路
代码实现
欧拉路径
欧拉路径的定义
欧拉路径的性质
欧拉回路基础
欧拉回路的定义

欧拉回路遍历了所有的边,也就意味着遍历了所有的点,但这并不能代表有欧拉回路的地方都有哈密尔顿回路的,如下图的例子。

欧拉回路的性质
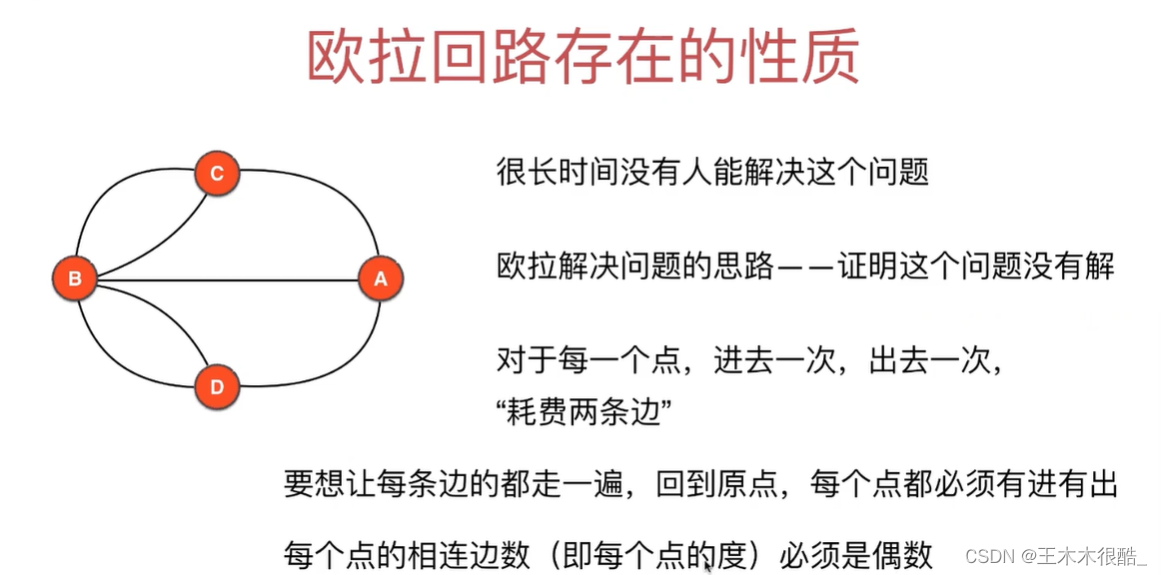 上图四个点的度数都是奇数,所以不存在欧拉回路。
上图四个点的度数都是奇数,所以不存在欧拉回路。
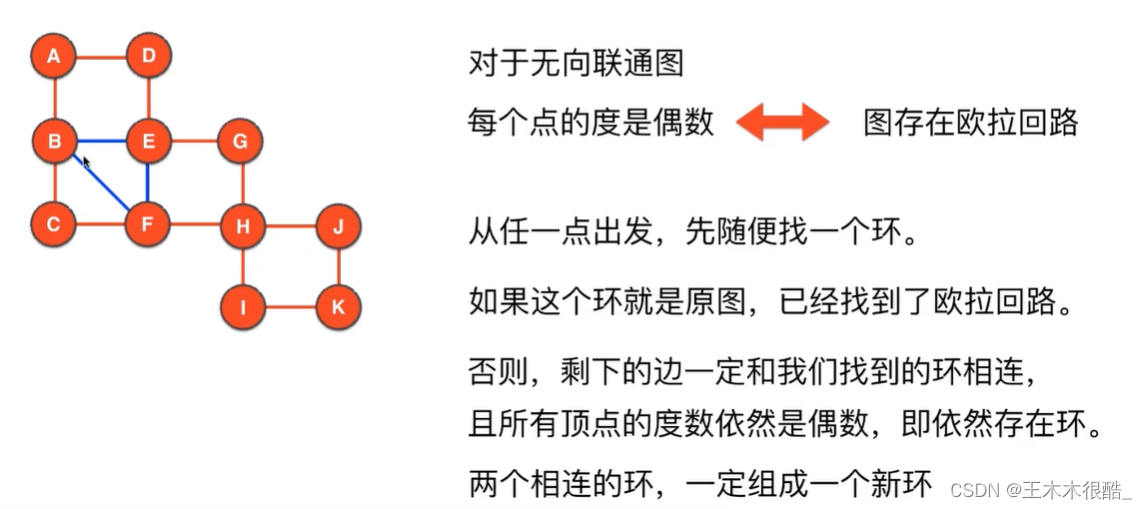
欧拉回路的条件:图是联通的、每个点的度数都是偶数。
判断图中是否存在欧拉回路的java代码实现
public class EulerLoop {private Graph G;public EulerLoop(Graph G){this.G = G;}public boolean hasEulerLoop(){//判断图的连通性//这里的CC类是判断图的连通分量的个数// 在我CSDN文章的图的深度优先遍历的六种应用附Java代码文章的第一个例子中有Java代码CC cc = new CC(G);if(cc.count() > 1) return false;if(G.degree(v) % 2 == 1) return false;return true;}
}
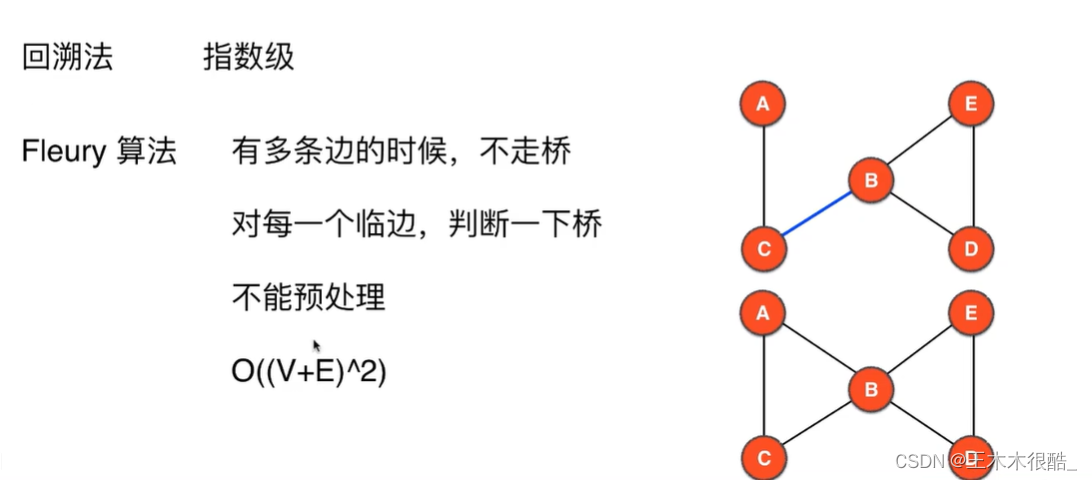
寻找欧拉回路的三个算法

前两个算法复杂度都比Hierholzer高得多,所以如果有参加竞赛的朋友要优先使用Hierholzer算法,尤其不要使用回溯法,几乎一定会超时。
Hierholzer算法
详细思路
Hierholzer算法使用两个栈,每走过一个顶点就把这个顶点压入curPath的栈中,每走过一条边就把这条边在图中删除,如下图的虚线表示。

我们先模拟走过的路径是A->B->C->A,最后回到A后发现无路可走了,我们就倒着把A、C出栈压入loop栈中,直到找到一个有其他路径可走的顶点,即B顶点。从B顶点出发还可以找到一个环,这个环和我们刚才删除的虚线环的公共顶点就是B顶点。
 我们继续从B顶点开始走,然后走过了这个新的环。
我们继续从B顶点开始走,然后走过了这个新的环。

接下来我们继续回头看,把curPath的数挨个检查是否还有哪个顶点有其他路径可走,若没有则压入loop栈中。

现在curPath这个栈空了,就代表我们把这个图遍历完了,现在loop栈中存储的顶点顺序就是倒序的欧拉回路的顺序,即A->B->D->E->B->C->A。我们把loop栈中的顶点依次出栈就得到了一种欧拉回路。
其实我们也可以把loop栈设置成一个ArrayList数组,因为正着看其实就是欧拉回路的另一种顺序,我们正着看反着看也没什么区别。以上就是整个Hierholzer算法的思路。这是一个线性级别的算法,只和图中有几条边有关系。

代码实现
我们在实现代码过程中要不断地删除走过的边,所以我们要在自己的Graph类中添加removeEdge()方法。 首先对传入的v、w进行合理性判断,然后因为是无向图,所以要各自删除掉v、w相邻顶点中的它们。

//我们选择使用的是最经典的非递归实现
//Hierholzer算法还存在递归实现,感兴趣的朋友可以试着去写一下
import java.util.ArrayList;
public class EulerLoop {private Graph G;public EulerLoop(Graph G){this.G = G;}public boolean hasEulerLoop(){//判断图的连通性//这里的CC类是判断图的连通分量的个数// 在我CSDN文章的图的深度优先遍历的六种应用附Java代码文章的第一个例子中有Java代码CC cc = new CC(G);if(cc.count() > 1) return false;if(G.degree(v) % 2 == 1) return false;return true;}public ArrayList<Integer>result(){ArrayList<Integer> res = new ArrayList<>();if(!hasEulerLoop()) return res;Graph g = (Graph) G.clone();int curv = 0;stack.push(curv);while(!stack.empty()){if(g.degree(curv) != 0){stack.push(curv);int w = g.adj(curv).iterator().next();//第一个元素g.removeEdge(curv, w);curv = w;}else{res.add(curv);curv = stack.pop();}}return res;}
}
欧拉路径
欧拉路径的定义
欧拉路径的性质

欧拉路径的起始点不能随便选了,只能选取度数是奇数的点。感兴趣的朋友可以自己试着实现欧拉路径的代码实现。


![[文件读取]shopxo 文件读取(CNVD-2021-15822)](https://img-blog.csdnimg.cn/9b3035be721947e5b78d090d6891996d.png)