文章目录
- 树与二叉树的转换
- 将二叉树转化为树
- 森林与二叉树的转化(二叉树与多棵树之间的关系)
- 二叉树转换为森林
- 森林的先序遍历
- 1)先序遍历
- 2)后序遍历
- 哈夫曼树的基本概念
- 森林转换成二叉树(二叉树与多棵树的关系)
树与二叉树的转换
将树转化为二叉树处理,利用二叉树的算法实现对树的操作。
由于树和二叉树都可以用二叉树链表做存储结构,则二叉链表的媒介可以导出与二叉树之间的对应关系。
给定一棵树,可以找到唯一的一棵二叉树与之对应。
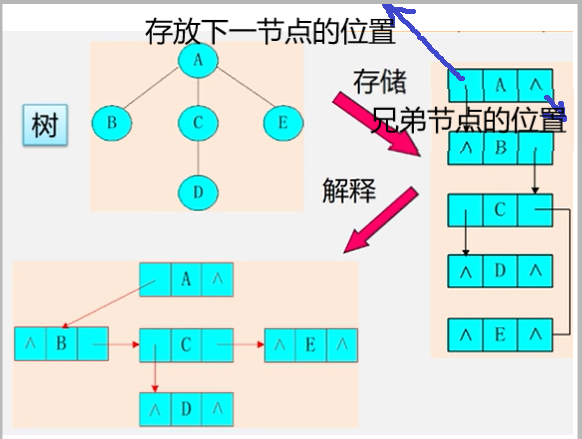
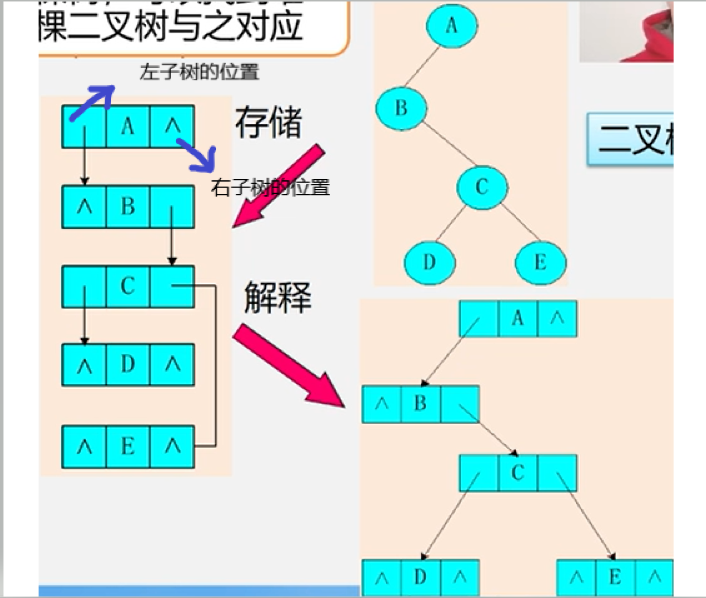
树变二叉树:兄弟相连留长子。
例如:
①兄弟相连
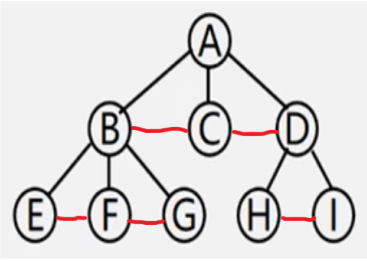
②留长子


将二叉树转化为树
左孩右右连双亲,去掉原来右孩线。
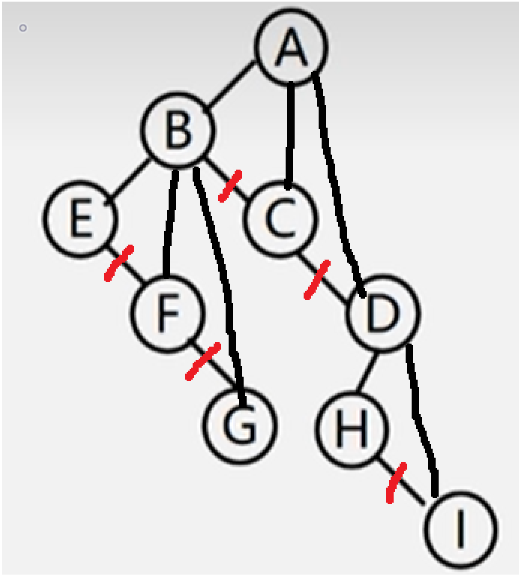
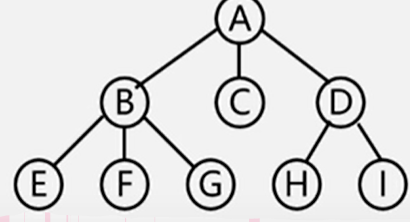
森林与二叉树的转化(二叉树与多棵树之间的关系)
树变二叉根相连
①将各棵树分别转换为二叉树。
②将每棵树的根结点用线相连。
③以第一棵树根结点为二叉树的根,再以根结点为轴心,顺时针旋转,构成二叉树结构。
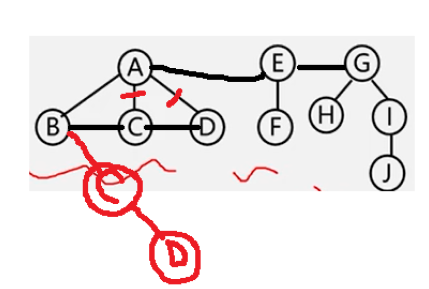
二叉树转换为森林
去掉全部右孩线,孤立二叉再还原。
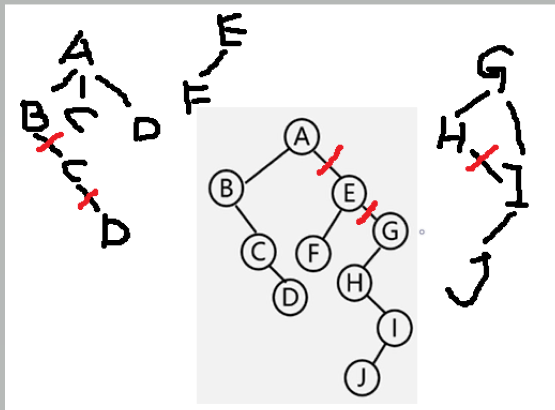
森林的先序遍历
1)先序遍历
- 若森林不空,则先访问根结点,然后从左向右的顺序,先遍历根结点的每一棵子树(依次从左至右对森林中的每一棵树进行先根遍历)。
- 树的先根遍历书序应该和二叉树的先序遍历顺序相同。
2)后序遍历
- 如果树非空,则按从左往右的顺序,后根遍历根结点的每一棵子树,然后访问根结点。
- 树的后根遍历顺序应与该树对应二叉树遍历顺序相同。
哈夫曼树的基本概念
- 路径:从树中的一个结点到另一个结点之间的分支构成这两个结点间的路径。
- 结点的路径长度:两结点路径上的分支数。
例如:
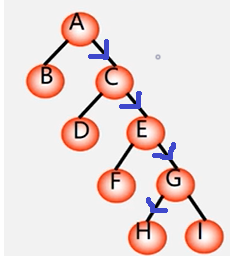 这里表示的是从A结点到H结点的路径,路径长度为4。
这里表示的是从A结点到H结点的路径,路径长度为4。 - 树的路径长度:从树根到每一个结点的路径长度之和。记作TL。
例如:
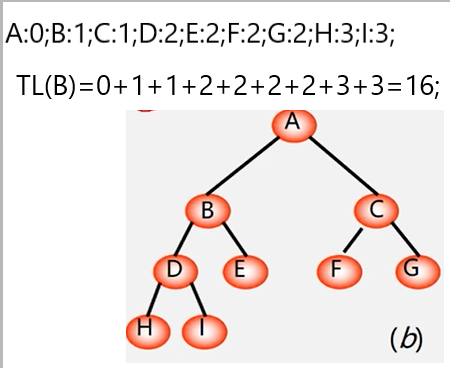
结点数目相同的二叉树中,完全二叉树的路径长度最短的二叉树。
森林转换成二叉树(二叉树与多棵树的关系)
①将各棵树分别转换为二叉树。