本次选题都为选择题。涉及到二叉树总结点和叶子结点的计算、二叉树的基本性质、根据二叉树的前序/后序和中序遍历画出二叉树、哈夫曼树等等…希望对你有帮助哦~😝
1.若一颗二叉树具有10个度为2的结点,5个度为1的结点,则度为0的结点个数为()
A.9 B.11 C.15 D.不确定
分析:本题为求解二叉树的度为0的结点个数,也就是求叶子结点。 在做此类题时,我们一般设两个未知数,即总结点n,和叶结点 n 0 {\ n_0} n0。 计算方法即,从两个角度看二叉树,从而列出等式。
二叉树的总结点树等于各不同性质结点之和即 n = n 0 + n 1 + n 2 {n=n_0+n_1+n_2} n=n0+n1+n2,从而, n = n 0 + 5 + 10 {n=n_0+5+10} n=n0+5+10。 二叉树的终结点数等于
结点的度*该性质结点的个数+1,(这个加的1即为这个树的根节点)即 n = 10 ∗ 2 + 5 ∗ 1 + 1 = 26 n=10*2+5*1+1=26 n=10∗2+5∗1+1=26,从而可以解得 n 0 = 11 n_0=11 n0=11.
故此题选B。
2.一颗完全二叉树上有1001个结点,其中叶子结点的个数为()
A.250 B.500 C.502 D.以上均不对
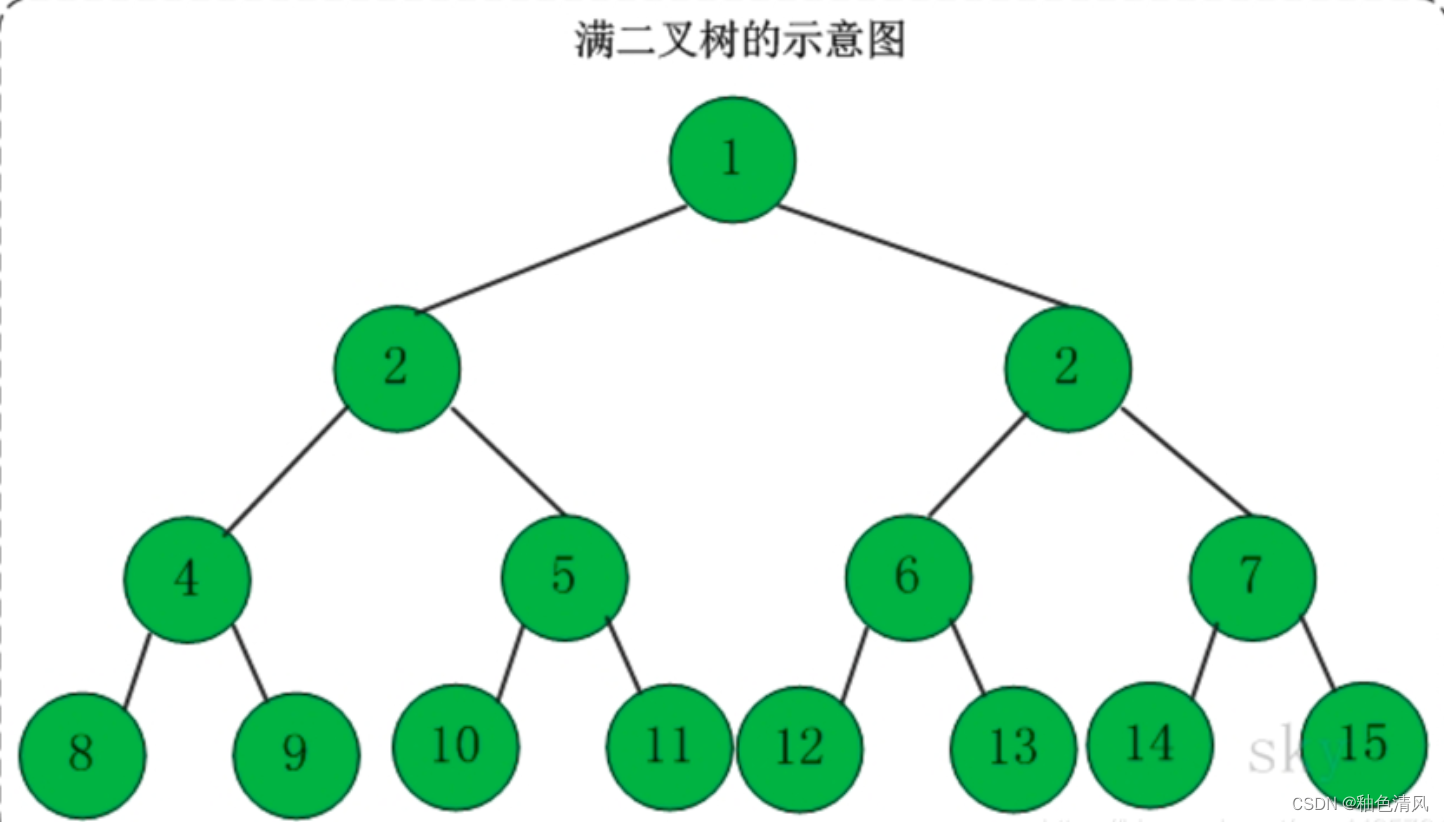
分析:本题涉及到了满二叉树的总结点数和层结点数的基本知识。
对于一颗满二叉树而言,若有k层,那么这颗满二叉树总结点数等于 2 k − 1 {2^k-1} 2k−1,
它在第k层的结点总数为 ( 2 k − 1 + 1 ) / 2 = 2 k − 1 (2^k-1+1)/2=2^{k-1} (2k−1+1)/2=2k−1。
那么具有k层的完全二叉树呢?它可以看作是k-1层满二叉树+最后一层叶结点。
对于本题,完全二叉树有1001个结点,我们推断:具有10层的满二叉树共有1023个结点,具有9层的满二叉树具有511个结点,所有该完全二叉树共有10层。
前9层共有结点数511,那么最后一层结点数为1001-511=490。但是这不是总的叶结点数。
我们还需要计算第9层的叶结点数。第九层的总结点数:(511+1)/2=256,第九层的叶结点数:256-490/2=11,故总的叶结点数为:490+11=501.
故本题选D。
3.具有10个叶子结点的完全二叉树中有()个度为2的结点。
A.8 B.9 C.10.D11
分析:根据二叉树的性质,对任何一棵二叉树T,如果其终端结点数为 n 0 n_0 n0,度为2的结点数为 n 2 n_2 n2,则 n 0 = n 2 + 1 n_0=n_2+1 n0=n2+1
对于这个性质呢,我是根据二叉树的两种结点的计算方法联立,消去 n 1 , n n_1,n n1,n,从而得到 n 0 n_0 n0和 n 2 n_2 n2的关系式。
故本题选B。
4.设给定权值结点总数有n个,那么哈夫曼树的结点总数为()。
A.不确定 B.2n C.2n+1 D.2n-1
分析:
这个题需要理解哈夫曼树的构造,哈夫曼树即是将森林中的树不断地合二为一,最终形成最优二叉树。我是根据基本的规律得出结论,给定权值结点的总数为2,那么哈夫曼树结点为3;给定权值结点的总数为3,那么哈夫曼树的结点为5…那么给定权值结点的总数为n,则哈夫曼树的结点总数为2n-1。
故本题选D。
5.用一组权值{3,6,8,10,11}构造一颗哈夫曼树,它的带权路径长度为()。
A.92 B.35 C.38 D.85
分析:本题的考察内容为哈夫曼树的构造以及基本的概念。
哈夫曼树构造的算法思想:
已知一组叶子结点的权值为 w 1 , w 2 , w 3 , . . . , w n w_1,w_2,w_3,...,w_n w1,w2,w3,...,wn则构造哈夫曼树的构成如下
①首先把n个叶子结点看作n棵树(仅有一个结点的二叉树),n棵树构成一颗森林。
②在森林中把权值最小和次小的两棵树合并成一棵树,该树结点的权值是两棵树根结点的权值之和,这时森林中就会减少一棵树。
③重复第②步直到森林中只有一颗二叉树为止。
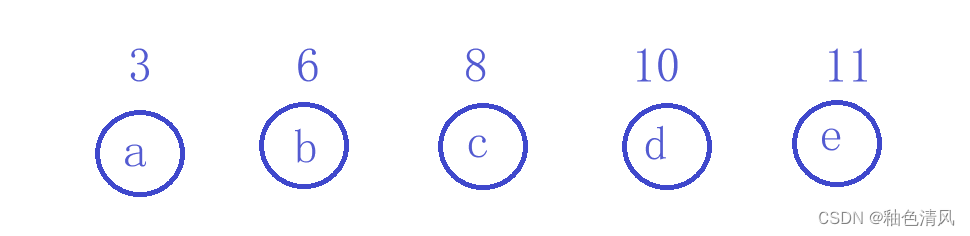
对于本题,设权值{3,6,8,10,11}对应的结点分别是a、b、c、d、e。
首先,这5棵树构成森林:
其次,选权值最小的a树和b合并成一棵树:
再次,选权值最小的也就是新构成的这个权值为9的树和c树构成合并成一颗新树:
然后,我们选择d树和e树合并成一棵树:
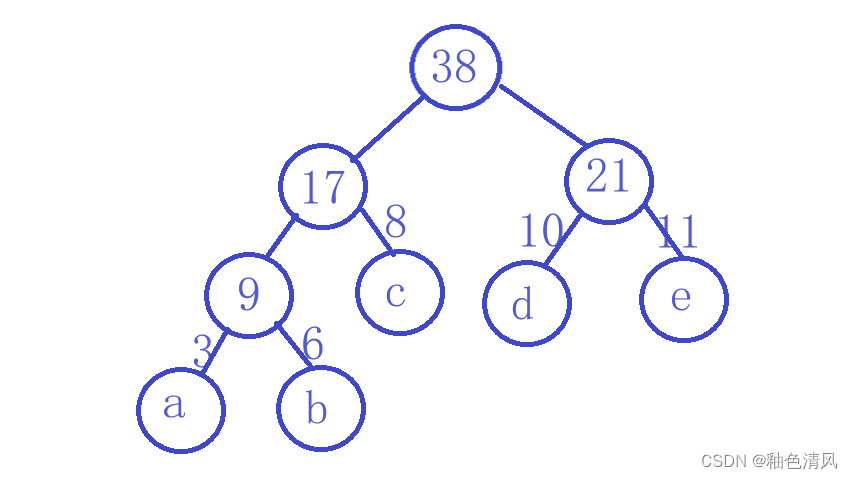
最后,我们将两棵树合并成一棵树:
我们现在已经构造好这一棵哈夫曼树,题目让求它的带权路径长度:
明确带权路径:
结点的带权路径长度:从根结点到该结点之间的路径长度与该结点的权的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和。记作:
W P L = ∑ k = 1 n w k l k WPL=\sum _{k=1}^n w_kl_k WPL=∑k=1nwklk
其中, w k w_k wk是权值, l k l_k lk是结点到根的路径长度,Weighted Path Length。
即: 3×3+3×6+2×8+2×10+2×11=85。
故本题选D。
6.下列有关二叉树的说法中,正确的是()
A.二叉树的度为2
B.一颗二叉树的度可以小于2
C.二叉树中至少有一个结点的度为2
D.二叉树中任何一个结点的度都为2
分析:二叉树中的任何结点的度都小于等于2,可以为0,1,2。
故此题选B
7.二叉树的第i层上最多含有结点数为()
A. 2 i 2^i 2i B. 2 i − 1 2^{i-1} 2i−1-1 C. 2 i − 1 2^{i-1} 2i−1 D. 2 i 2^i 2i-1
分析:二叉树的基本性质,第i层上最多含有 2 i − 1 2^{i-1} 2i−1个结点。
故本题选C。
8.一颗具有n个结点的完全二叉树的深度为()
A. [ log 2 n ] + 1 [\log_2n]+1 [log2n]+1 B. log 2 n + 1 \log_2n+1 log2n+1 C.[ log 2 n \log_2n log2n] D. log 2 n − 1 \log_2n-1 log2n−1
分析:二叉树的基本性质,一颗具有n个结点的完全二叉树的深度为 [ log 2 n ] + 1 [\log_2n]+1 [log2n]+1
故本题选A。
9.在一棵深度为k的满二叉树中,结点总数为()
A. 2 k − 1 2^{k-1} 2k−1 B. 2 k 2^k 2k C. 2 k − 1 2^k-1 2k−1 D.[ log 2 k \log2^k log2k]+1
分析:二叉树的基本性质,在一棵深度为k的满二叉树中,结点总数为 2 k − 1 2^k-1 2k−1
故此题选C。
10.一颗二叉树的先序遍历序列为ABCDEFG,它的中序遍历序列可能是() A.CABDEFG B.ABCDEFG C.DACEFBG D.ADCEFG
分析:这个题,可以从很多方面进行排除。
首先,我们可以很确定的是这棵树的根节点为A。
我比较喜欢采用中序遍历的特点,将这棵树可能的形状进行想象,从而排除。
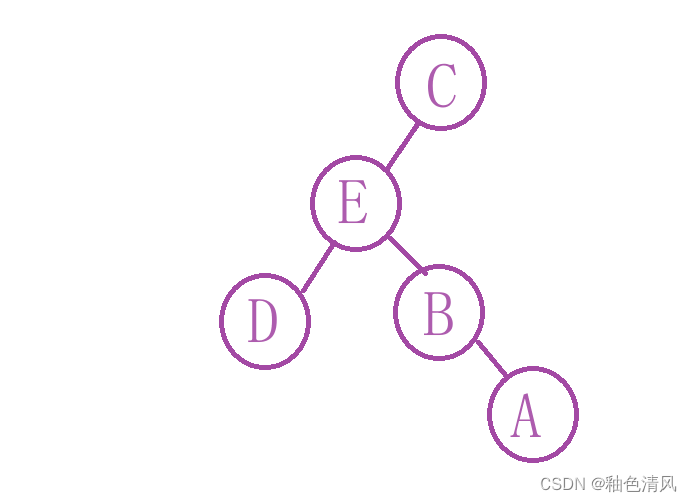
中序遍历的特点就是,将一颗树压扁之后,即压制同一水平线,就是中序遍历的结果。
例如这颗二叉树,我将其压扁,之后的排序就是,dgbeafhc。
根据中序遍历的特点,我们逐个排除选项。
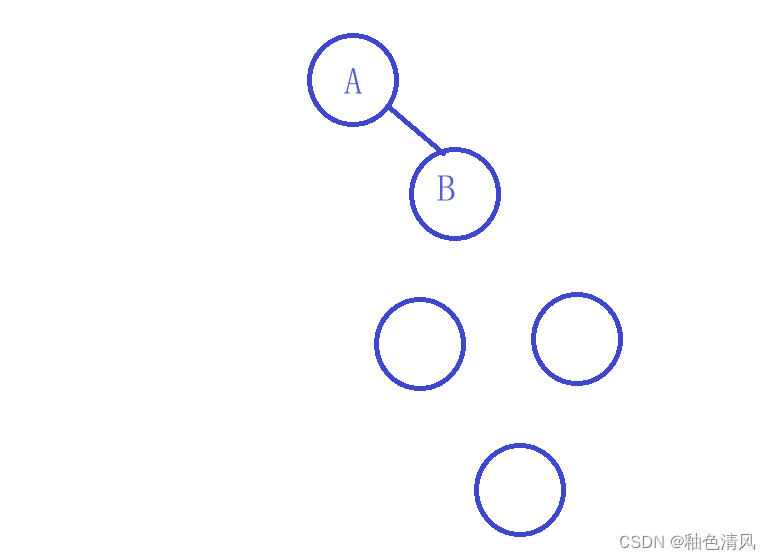
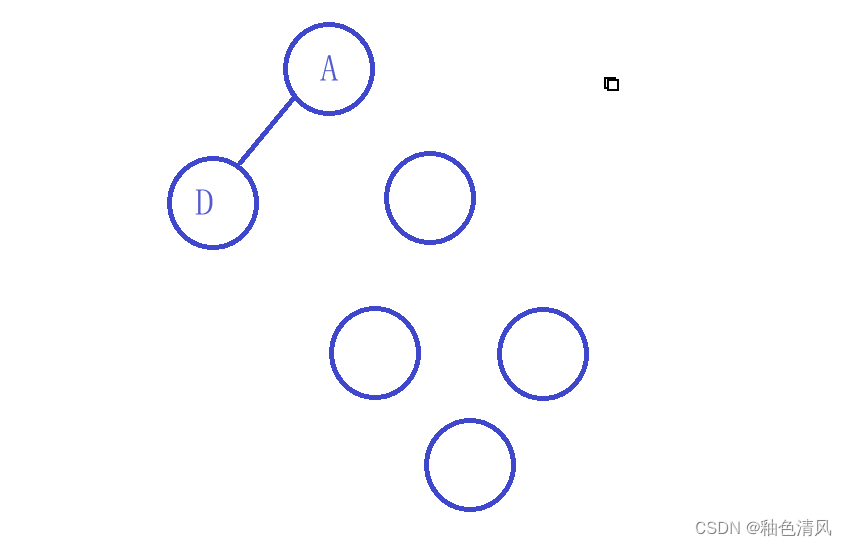
对于A选项,CABDEFG,则这颗二叉树部分一定是
C为A的左子树。右边我们可以不先进行判断,如果是这样的话,那么它的前序遍历一定是AC…所以排除A选项。
对于B选项,ABCDEFG,这棵树的部分一定是:
即这棵树只有右子树,没有左子树。那么对应它的先序遍历AB…,首先基本的看不出错误。
对于C选项,DACEFBG,它的部分一定是,
那么它对应的前序遍历一定是 DA…,所以排除C选项。
对于D选项,ADCEFG那么它对应的二叉树的部分一定是:
那么它对应的前序遍历一定是 AD…不符,所以排除D选项。
故此题选B。
11.已知某二叉树的后序遍历序列为DABEC,中序遍历序列为DEBAC,它的先序遍历序列是()。
A.ACBED B.DECAB C.DEABC D.CEDBA
分析:此类题目是经典根据中序遍历和先序/后序遍历得出后序/先序遍历的题。此类题需要我们根据已知的信息发出这颗二叉树,从而得出它的先序/后序遍历。
做这类题都是根据先序、中序、后序遍历的特点分析:先序顺序即:根->左子树->右子树,中序遍历为:左子树->根->右子树,后序遍历为:左子树->右子树->根。
对于本题,根据后序遍历,得出根节点C。
根据我们画出来的二叉树,从而得出它的先序遍历是 CEDBA。
故本题选择D。
12.二叉树的先序遍历序列为EFHIGJK,中序遍历为HFIEJKG,该二叉树根的右子树的根是()
A.E B.F C.G D.H
分析:同上题一样,我们先画出此二叉树,从而得出结论。
我们画出此二叉树。从而可以知道该二叉树的右子树的根为G。
故此题选C。
13.某二叉树的先序序列和后序序列正好相反,则该二叉树一定是()的二叉树。
A.空或只有一个结点 B.任一结点无左子树 C.高度等于其结点数 D.任一结点无右子树
分析:先序序列:根->左子树->右子树
反过来:右子树->左子树->根
后序序列:左子树->右子树->根
因此树只有根结点,或者根结点只有左子树或右子树,依此类推,其子树有同样的性质,任意结点只能有一个孩子,才能满足先序序列和后序序列正好相反。树形应该为一个长链。
所以选B。
14.在有n个结点的二叉树中的二叉链表表示中,空指针数()。
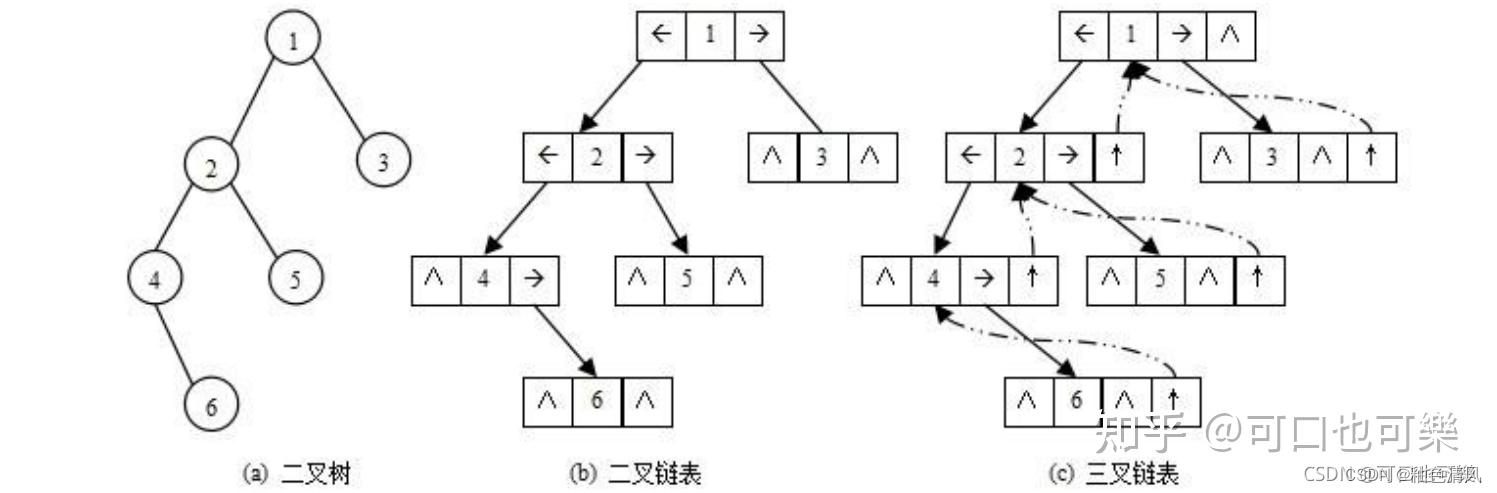
A.不定 B.n+1 C.n Dn-1分析:二叉链表即如下图所示。
在n个结点中,有叶子结点,其两个指针域都是空指针。有有一个孩子的结点,其有一个指针域不为空,有一个指针域为空。有有两个孩子的结点,其两个指针域都不为空。那么空指针数等于叶子结点数×2+有一个孩子的结点数。
设所求空指针数为m,则 m = 2 n 0 + n 1 m=2n_0+n_1 m=2n0+n1。
我仍然根据两个基本的方程进行联立,从而得到:
故本题选B。
15.若某二叉树有20个叶子结点,有20个结点仅仅有一个孩子,则该二叉树的总结点数是()。
A.40 B.55 C.59 D.61
分析:本题是求二叉树的总结点树。此类题目,我们仍然从两个角度去列方程。> 首先,先设总结点树为n,设有两个孩子的结点树为 n 2 n_2 n2:> 则 n = n 0 + n 1 + n 2 = 20 + 20 + n 2 n=n_0+n_1+n_2=20+20+n_2 n=n0+n1+n2=20+20+n2> n= 20 ∗ 1 + n 2 ∗ 2 + 1 20*1+n_2*2+1 20∗1+n2∗2+1> 联立解得n=59。
故本题选C。
16.假设一颗二叉树中,双分支结点数为15,单分支结点数为30个,则叶子结点数为()个。
A.40 B.55 C.59 D.61
分析:由题可以转化,有两个孩子的结点数为15,有一个孩子的结点数为30。
我们同上个题目一样,列方程解出。
设总结点数为n,叶子结点数为 n 0 n_0 n0.
则有 n = n 0 + n 1 + n 2 = n 0 + 30 + 15 n=n_0+n_1+n_2=n_0+30+15 n=n0+n1+n2=n0+30+15
n = 15 ∗ 2 + 30 ∗ 1 + 1 = 61 n=15*2+30*1+1=61 n=15∗2+30∗1+1=61
从而解得, n 0 n_0 n0=16。
故本题选B。
17.按照二叉树的定义,具有三个结点的二叉树有()种。
A.3 B.4 C.5 D.6
分析:二叉树是有序树,因而具有三个节点的二叉树有以下五种:
故本题选C。
18.根据先序序列ABDC和中序序列DBAC确定对应的二叉树,该二叉树()。
A.是完全二叉树 B.不是完全二叉树 C.是满二叉树 D. 不是满二叉树
分析:我们根据先序遍历和中序遍历画出此二叉树即可。
由树的形态可知,该树为完全二叉树。
故本题选A。
19.某二叉树的中序遍历为ABCDEFG,后序遍历为BDCAFGE,则其左子树中结点数目为()
A.3 B.2 C.4 D.5
分析:题目只要求 求左子树中的结点数目即可。所以我们可以直接进行分析,不需要具体画出此二叉树。 根据后序遍历,我们可以得之,这棵树的根节点为E,根据根节点E,从中序遍历结果中即可看出,左子树的所有结点为ABCD,右子树的所有结点为FG。
故本题选择C。
20.将一颗有100个结点的完全二叉树从根这一层开始,每一层上从左到右一次对结点进行编号,根节点的编号为1,则编号为49的结点的左孩子的编号为()
A.98 B.99 C.50 D.48
分析: 2 5 < 49 < 2 6 2^5<49<2^6 25<49<26,故编号为49的结点在第5层上面。
并且可以得之,编号为49的结点为第5层的第49-32+1=18个结点。
第6层的结点从64开始,63+17*2=97,则编号为49的结点的左孩子的编号为98。
故本题选A。
21.树最适合用来表示()
A.有序数据元素
B.无序数据元素
C.元素之间具有分支层次关系的数据
D.元素之间无关联的数据
分析:树型数据结构是一种重要的非线性数据结构,是以分支关系定义的层次结构。故树适合用于用来表示元素之间具有分支层次关系的数据。
故本题选C。
22.下面说法中正确的是()。
A.度为2的树是二叉树。
B.度为2的有序树是二叉树。
C.子树有严格左右之分的树是二叉树。
D.子树有严格之分,且度不超过2的树是二叉树。
分析:二叉树的度可以为1或0.比如:
一个只有根结点的树的度为0,左边这个二叉树的度为1。故子树有严格之分,且度不超过2的树为二叉树。
本题选D。