【LeetCode热题100】打卡第32天：最长连续序列&只出现一次的数字&单词拆分&环形链表

⛅前言

大家好，我是知识汲取者，欢迎来到我的LeetCode热题100刷题专栏！

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。在此专栏中，我们将会涵盖各种类型的算法题目，包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等，并会提供详细的解题思路以及Java代码实现。如果你也想刷题，不断提升自己，就请加入我们吧！QQ群号：827302436。我们共同监督打卡，一起学习，一起进步。

LeetCode热题100专栏🚀：LeetCode热题100

Gitee地址📁：知识汲取者 (aghp) - Gitee.com

题目来源📢：LeetCode 热题 100 - 学习计划 - 力扣（LeetCode）全球极客挚爱的技术成长平台

PS：作者水平有限，如有错误或描述不当的地方，恳请及时告诉作者，作者将不胜感激

最长连续序列

🔒题目

原题链接：128.最长连续序列

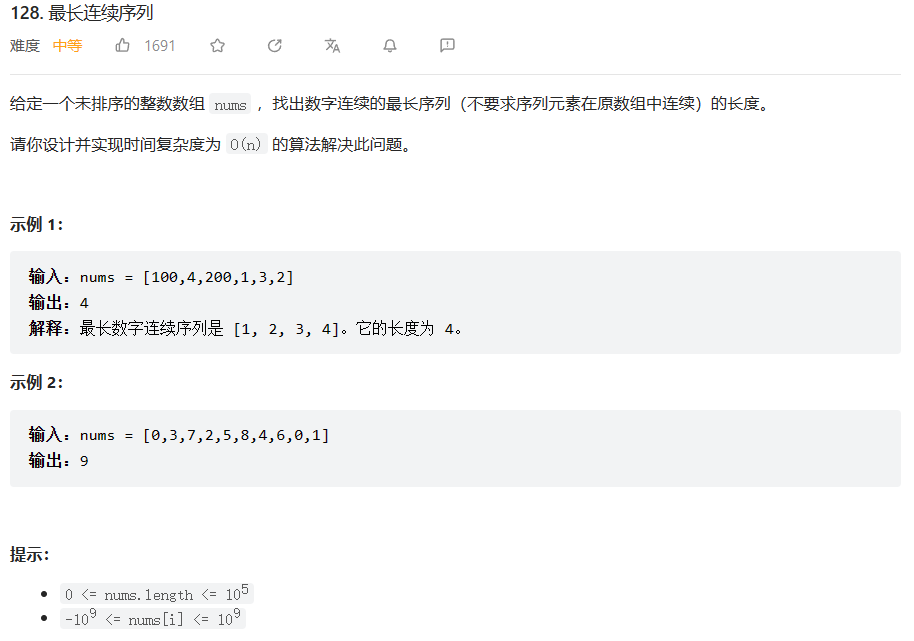
🔑题解

• 解法一：排序

  class Solution {public int longestConsecutive(int[] nums) {int len = nums.length;if (len <= 1){return len == 0 ? 0 : 1;}Arrays.sort(nums);int i = 1;int max = 0;int count = 1;while (i < len) {int dif = nums[i] - nums[i - 1];if (dif == 1) {// 差值为1，相邻元素连续count++;} else if (dif == 0) {// 差值为0，相邻元素相同} else {// 相邻元素有间隔，重新计数count = 1;}i++;max = Math.max(max, count);}return max;}
  }
  

  复杂度分析：

  • 时间复杂度：$O(nlogn)$，Arrays.sort内部实现是快排，时间复杂度是$nlogn$，while循环的时间复杂度是$n$，所以总的来说的$nlognn$
  • 空间复杂度：$O(1)$，没有占用额外的空间，空间开销是常数

  其中 $n$ 为数组中元素的个数

  PS：这段代码的时间复杂度没有达到$O(n)$，但是经过提交发现时间和空间的占用居然还超过了官方时间复杂度为$O(n)$的代码😳，这可能是示例数据的原因，一般而言并不是说时间复杂度越高效率就越第（比如动态规划时间复杂度可能有$O(n^2)$，但可能比一些时间复杂度为$O(n)$的代码还要快，这里也是一样）

• 解法二：哈希表

  通过Set集合去重，然后利用contains方法检索下一个数是否在Set集合中，但是会发现居然超时了！

  class Solution {public int longestConsecutive(int[] nums) {// 利用Set集合进行去重Set<Integer> set = new HashSet<>();for (int i = 0; i < nums.length; i++) {set.add(nums[i]);}int max = 0;for (Integer i : set) {int count = 1;int next = i + 1;while (set.contains(next)) {// 当前数字的后一个数字在Set集合中，len+1next++;count++;}max = Math.max(max, count);}return max;}
  }
  

  复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(n)$

  其中 $n$ 为数组中元素的个数

  代码优化：时间优化

  上面代码超时了，这是由于出现了大量重复的计算，比如：Set集合中是{1，2，3，6，7，9}，在计算元素 1 的最大连续数时，其实就已经计算过了 2 和 3 的最大连续数，所以这里我们可以进行一个过滤（有点像剪枝操作），避免重复计算，那么该如何过滤呢？其实我们只需要 添加一个 !set.contains(i-1)即可，也就是如果当前元素的上一个数在Set集合中存在，就说明当前元素的最大连续值已经计算过了

  class Solution {public int longestConsecutive(int[] nums) {// 利用Set集合进行去重Set<Integer> set = new HashSet<>();for (int i = 0; i < nums.length; i++) {set.add(nums[i]);}int max = 0;for (Integer i : set) {int count = 1;if (!set.contains(i - 1)) {int next = i + 1;while (set.contains(next)) {// 当前数字的后一个数字在Set集合中，count+1next++;count++;}}// 更新最大连续序列的长度max = Math.max(max, count);}return max;}
  }
  

• 解法三：动态规划

  略……详情参考【超小白】哈希集合/哈希表/动态规划/并查集四种方法，绝对够兄弟们喝一壶的！ - 最长连续序列 - 力扣（LeetCode）

• 解法四：并查集

  略……感兴趣的可以参考上面的链接

只出现一次的数字

🔒题目

原题链接：136.只出现一次的数字

🔑题解

• 解法一：暴力

  这种暴力是我最开始想到的，利用map进行映射时间复杂度相对较小，还有一种更加暴力的方法双重for循环，时间复杂度高达$O(n^2)$

  class Solution {public int singleNumber(int[] nums) {Map<Integer, Integer> map = new HashMap<>();for (int i = 0; i < nums.length; i++) {int value = map.getOrDefault(nums[i], 0);if (value <= 1) {map.put(nums[i], value + 1);}}int ans = 0;for (int key : map.keySet()) {int value = map.get(key);if (value == 1) {ans = key;}}return ans;}
  }
  

  复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(n)$

  其中 $n$ 为数组中元素的个数

• 解法二：排序

  class Solution {public int singleNumber(int[] nums) {Arrays.sort(nums);int ans = Integer.MIN_VALUE;for (int i = 0; i < nums.length-2; i+=2) {if (nums[i] != nums[i + 1]) {ans = nums[i];break;}}return ans == Integer.MIN_VALUE ? nums[nums.length-1] : ans;}
  }
  

  复杂度分析：

  • 时间复杂度：$O(nlogn)$，Arrays.sort底层是快排，快排的时间复杂度是 $nlogn$
  • 空间复杂度：$O(1)$

  其中 $n$ 为数组中元素的个数

• 解法三：位运算（按位异或）

  这个太强了，没有想到这方面，但是一看就豁然开朗（只能说见识太短了，或者说经验不足）。我们需要明确异或^运算的特点：同为假（同真同假都为假），不同为真（一真一假为真），通过它的特点我们可以有以下结论：

  1. 交换律：a^b^c=a^c^b
  2. 与0异或结果为本身：0^n=n
  3. 相同数异或为0：n^n=0

  class Solution {public int singleNumber(int[] nums) {int ans = 0;for (int i : nums) {ans ^= num;}return ans;}
  }
  

  复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(n)$

  其中 $n$ 为数组中元素的个数

单词拆分

🔒题目

原题链接：139.单词拆分

fi

🔑题解

• 解法一：DFS（超时，36/46，10个用例没通过）

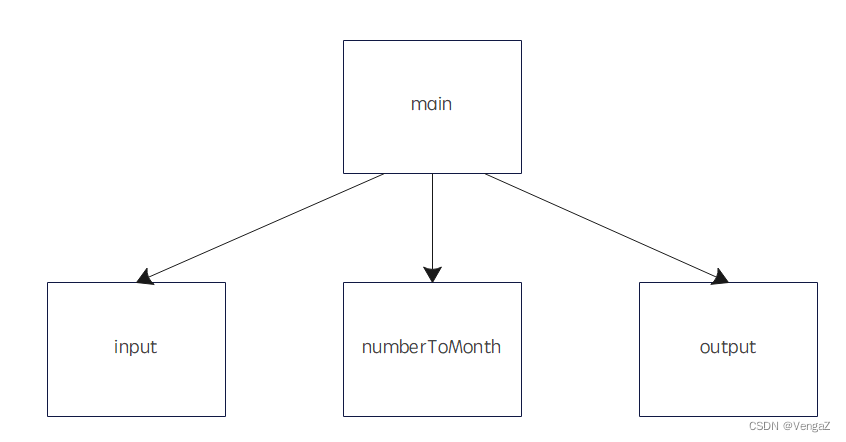
  DFS 解题示意图：

  class Solution {private boolean f = false;public boolean wordBreak(String s, List<String> wordDict) {StringBuilder path = new StringBuilder();dfs(s, wordDict, path);return f;}private void dfs(String s, List<String> wordDict, StringBuilder path) {if (s.equals(path.toString())){// 当前路径组成了目标值，结束递归f = true;return;}if (path.length()> s.length() || !s.substring(0, path.length()).equals(path.toString())){// 当前路径组成字符串的长度超过了目标值长度// 当前路径组成字符串的最后字符不等于目标值最后那段字符return;}for (int i = 0; i < wordDict.size(); i++) {String str = wordDict.get(i);path.append(str);// 往下遍历下一个节点dfs(s, wordDict, path);// 恢复现场，用户回溯path.delete(path.length()-str.length(), path.length());}}
  }
  

  复杂度分析：

  • 时间复杂度：$O(n\ast m)$，在每个递归步骤中，我们都要遍历整个字典 wordDict 中的单词。所以，对于每个单词，我们需要执行一次递归调用。因此，总的递归调用次数是 O(N)，其中 n 是字典中的单词数量。除此之外，我们还需要比较字符串 s 的前缀和当前路径 path 的前缀，这需要 O(m) 的时间，其中 m 是字符串 s 的长度。因此，该算法的时间复杂度为 O(n*m)
  • 空间复杂度：$O(m)$，递归的最大深度应该是$m$，所以空间复杂度是$O(m)$

  其中 $n$ 为字典中单词的数量，$m$是字符串的长度

  代码优化：时间优化

  前面直接使用暴力DFS超时了，所以我们需要对DFS进行优化，而DFS优化策略一般是剪枝，这里我们需要使用 记忆索索，

  实现剪枝，具体代码如下：

• 解法二：哈希表

  这个太强了，时间复杂度直接变成$O(n)$，它是利用Map的Key不能重复的特性，来判断元素是否符合要求。

  复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(n)$

  其中 $n$ 为数组中元素的个数

环形链表I

🔒题目

原题链接：141.环形链表I

🔑题解

• 解法一：快慢指针

  由于这个题目是二刷了，所以顺其自然以下就想到了快慢指针这个解法，这个类似于物理里面的相对速度，一个指针比另一个指针要快一个速度，这样如果链表中有环，快指针一定会出现在慢指针的后面，如果没有环则快指针直接就到底了，实现起来也比较简单😄，看来坚持每天刷题还是有一定作用的，不至于遇到这个题目没有任何的思绪

  public class Solution {public boolean hasCycle(ListNode head) {if (head == null) {return false;}ListNode slow = head;ListNode fast = head;while (fast != null) {if (fast.next == slow) {// fast走到了slow的后面，说明链表中有环return true;}slow = slow.next;// fast比slow多走一步fast = fast.next;if (fast != null){// 防止NPEfast = fast.next;}}return false;}
  }
  

  复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(1)$

  其中 $n$ 为链表中节点的数量

• 解法二：利用Set集合不重复的特点

  这种方式十分的暴力简单🤣，效率没有快慢指针快

  public class Solution {public boolean hasCycle(ListNode head) {Set<ListNode> seen = new HashSet<>();while (head != null) {if (!seen.add(head)) {return true;}head = head.next;}return false;}
  }
  

  复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(n)$

  其中 $n$ 为链表中节点的数量