一题带你写出图论算法模板！！！-编程知识

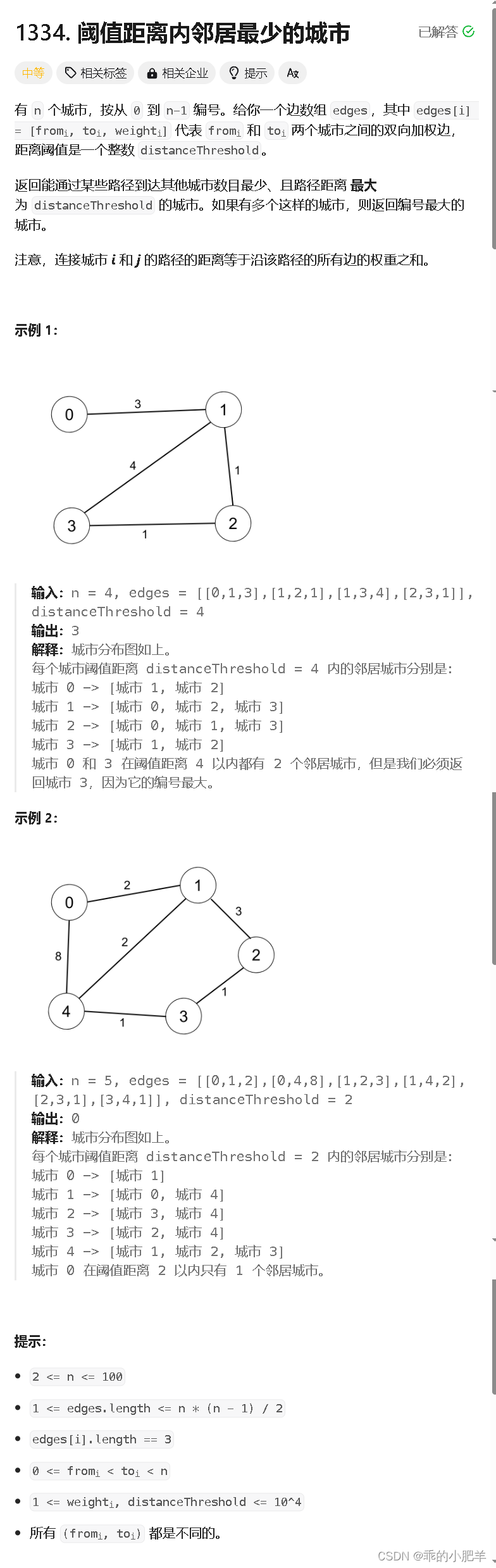
这题是道基础的图论算法题目

注释很重要！！！！！！！

在做这道题之前，我们先了解一下基础的图论算法吧！！！

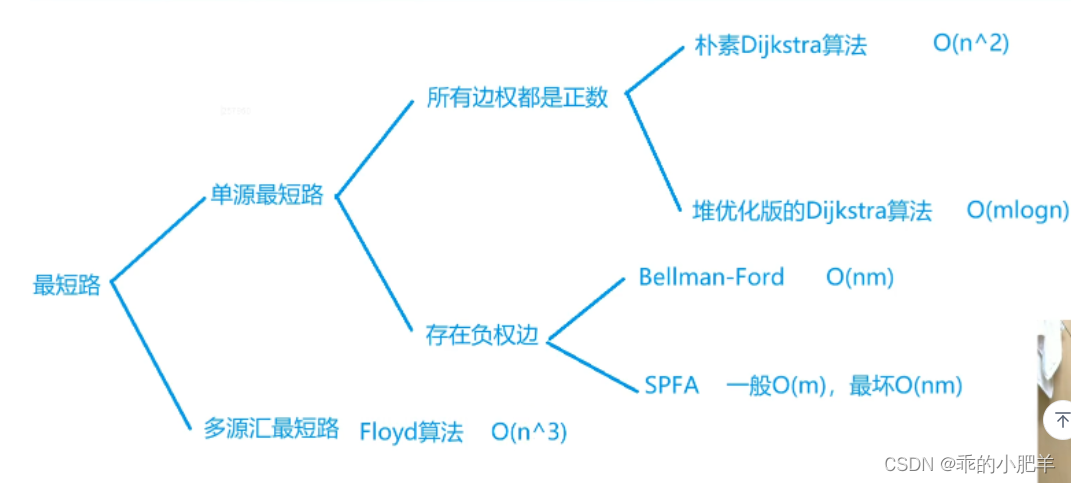
1.floyd：

这样可以求出所有点到任意一点的最短路径和距离

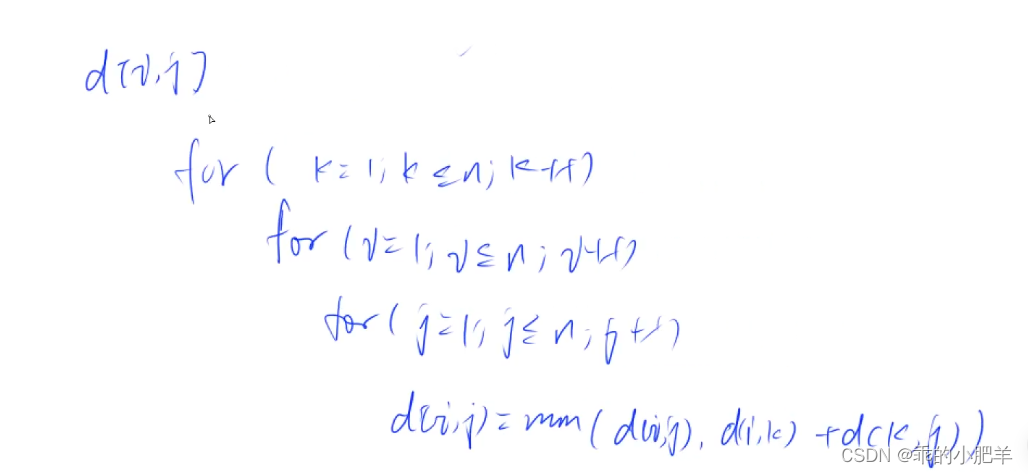
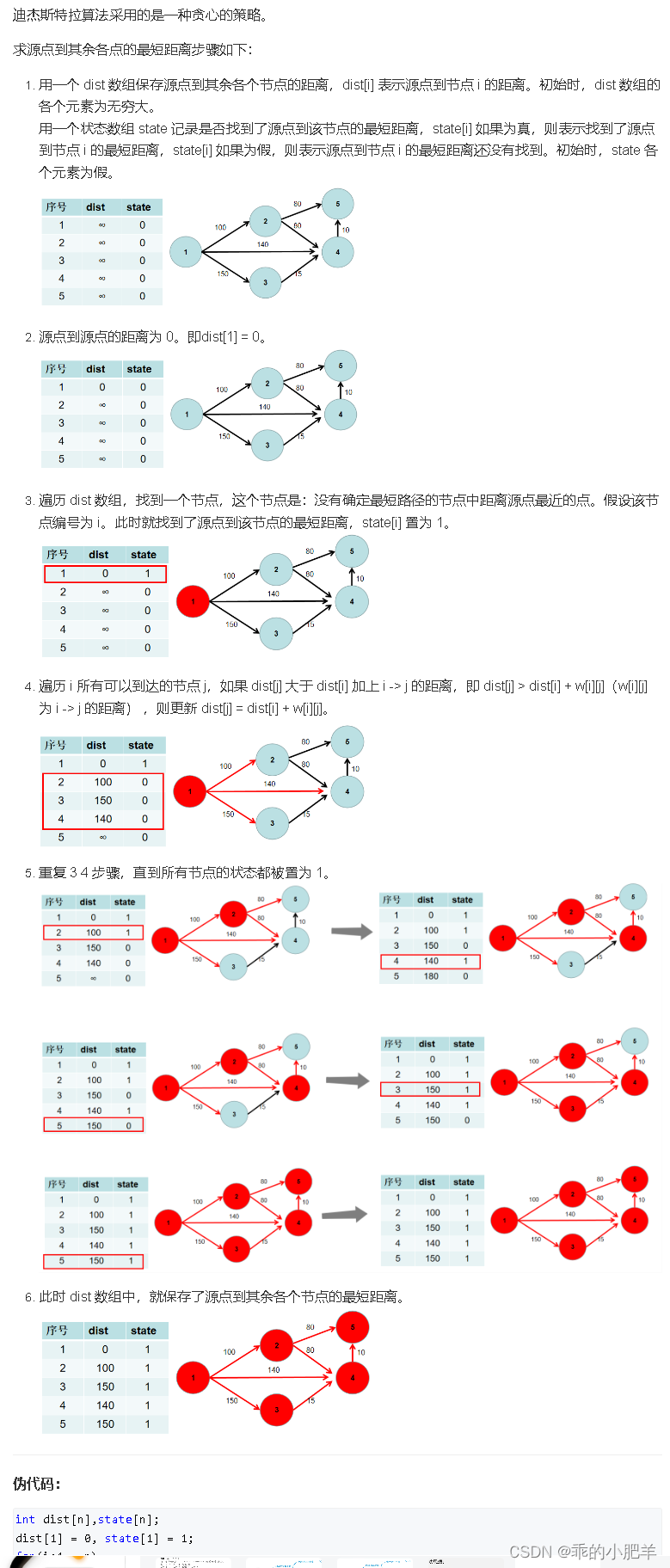
dijkstra：

最短路问题考察的是我们如何抽象成一个模型

图论的题侧重点在于抽象

难点在建图！！！！

2.朴素Dijstra算法

Dijkstra算法算是贪心思想实现的，首先把起点到所有点的距离存下来找个最短的，然后松弛一次再找出最短的，所谓的松弛操作就是，遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近，如果更近了就更新距离，这样把所有的点找遍之后就存下了起点到其他所有点的最短距离

3.dijkstra算法（堆优化，c++直接用STL优先队列）

能使用的核心是堆中出来的点一定是最小的，且不会被更新的

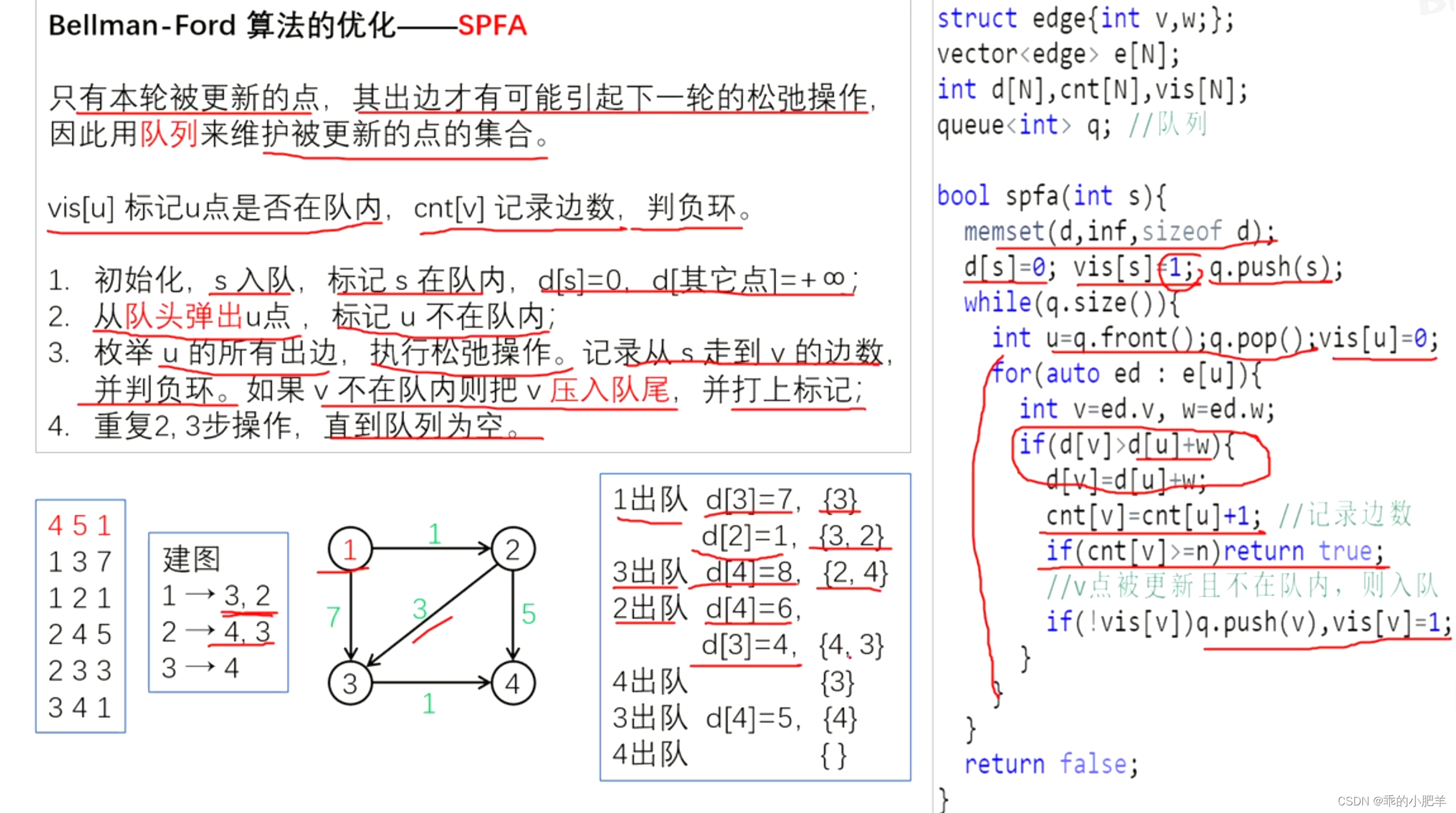
4.spfa算法（没有负环就可以用）

可以用于适合dijkstra解决的问题

floyd方法:

class Solution {
public:int dist[1100][1100];void floyd(int n){//floyd本质是试点探测法for(int k = 0;k < n;k++)for(int i = 0;i < n;i++)for(int j = 0;j < n;j++){//试点探测dist[i][j] = min(dist[i][j],dist[i][k] + dist[k][j]);}}int ans[1110];int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {//这题一看求的就是多源最短路//计算出当前点到所有点的最短距离，小于distance距离的点加入到当前点的数组的中//多源最短路有floyd算法，最常用的算法//也可以用单源最短路算法spfa和dijkstra，bellmanford(一般不用，复杂度有点高)//1.dijkstra算出当前点到所有点的距离，小于distance距离的点加入到当前点的数组的中//再遍历下一个点，往返加入int m = edges.size();memset(dist,0x3f,sizeof(dist));//初始化为无穷，方便后续试点判断的时候，不把无穷的点加入//无向图for(int i = 0;i < m;i++){int a = edges[i][0];int b = edges[i][1];int c = edges[i][2];dist[a][b] = c;dist[b][a] = c;dist[a][a] = 0;dist[b][b] = 0;}floyd(n);int min_val = 0x3f3f3f3f;for(int i = 0;i < n;i++){cout<<i<<" ";for(int j = 0;j < n;j++){if(j == i) continue;if(dist[i][j] <= distanceThreshold) ans[i]++;}min_val = min(ans[i],min_val);cout<<ans[i]<<endl;}int res = -0x3f3f3f3f;for(int i = 0;i < n;i++){if(ans[i] == min_val && res < i) res = i;}return res;}
};

spfa方法：

class Solution {
public:int h[11100],w[11100],ne[11100],e[11100],idx = 0;int dist[11100];void add(int a,int b,int c){e[idx] = b,ne[idx] = h[a],w[idx] = c,h[a] = idx++;}queue<int> q;int st[1100];void spfa(int start){dist[start] = 0;q.push(start);//队列里放着要被更新的点，这个点要去松弛边st[start] = 1;while(!q.empty()){ auto t = q.front();q.pop();st[t] = 0;//该点出队更新其他点(松弛边)for(int i = h[t];i != -1;i = ne[i]){int b = e[i];int c = w[i];if(dist[b] > dist[t] + c){dist[b] = dist[t] + c;if(!st[b]) {q.push(b);//如果该点不在队列里面，并且连接该点的边又被更新，那么我们一定要加入到队列，再更新一次st[b] = 1;}}}}//题目没有负权边}int ans[1100];int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {memset(h,-1,sizeof(h));int m = edges.size();for(int i = 0;i < m;i++){int a = edges[i][0];int b = edges[i][1];int c = edges[i][2];add(a,b,c);add(b,a,c);}int min_val = 0x3f3f3f3f;for(int i = 0;i < n;i++){int start = i;memset(dist,0x3f,sizeof(dist));memset(st,0,sizeof(st));spfa(start);for(int j = 0;j < n;j++){if(j == start) continue;if(dist[j] <= distanceThreshold) ans[start]++;}cout<<start<<" "<<ans[start]<<endl;min_val = min(ans[start],min_val);}cout<<min_val<<endl;int res = -0x3f3f3f3f;for(int i = 0;i < n;i++){if(ans[i] == min_val && res < i) res = i;}return res;}
};

dijkstra方法：

class Solution {
public:int h[11100],w[11100],ne[11100],e[11100],idx = 0;int dist[11100];void add(int a,int b,int c){e[idx] = b,ne[idx] = h[a],w[idx] = c,h[a] = idx++;}//st数组保存的是已经被拿来更新过的点//我们每次取的就是，从未被更新过的点集中选出一个离更新过的点的点集(距离点集中的源点最近)最近的点//更新过的点的点集我们记为V,未更新过的点的点集记为Eint st[11000];void dijkstra(int start,int n){dist[start] = 0;for(int i = 0;i < n;i++){  int t = -1;for(int j = 0;j < n;j++){if(!st[j] && (t == -1 || dist[t] > dist[j])) //要拿出的点必须是未更新过的点集中的点，//并且是离V的点集(距离点集中的源点)，也就是距离源点距离最短的点{t = j;}}st[t]  = 1;for(int i = h[t];i != -1;i = ne[i])//用t去更新邻边{int b = e[i];int c = w[i];dist[b] = min(dist[b],dist[t] + c); }}}int ans[1100];int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {memset(h,-1,sizeof(h));int m = edges.size();for(int i = 0;i < m;i++){int a = edges[i][0];int b = edges[i][1];int c = edges[i][2];add(a,b,c);add(b,a,c);}int min_val = 0x3f3f3f3f;for(int i = 0;i < n;i++){int start = i;memset(dist,0x3f,sizeof(dist));memset(st,0,sizeof(st));dijkstra(start,n);for(int j = 0;j < n;j++){if(j == start) continue;if(dist[j] <= distanceThreshold) ans[start]++;}cout<<start<<" "<<ans[start]<<endl;min_val = min(ans[start],min_val);}cout<<min_val<<endl;int res = -0x3f3f3f3f;for(int i = 0;i < n;i++){if(ans[i] == min_val && res < i) res = i;}return res;}
};

模板题：

#include <iostream>
//因为题目给出500个点，100000条边，说明是个稠密图
//所以我们用邻接矩阵去存储
//朴素dijkstra算法
//三步骤
//1.初始化dist[1] = 0，其余的为正无穷，可以用0x3f3f3f表示
//2for循环n次
//3.遍历dist数组，找到一个节点，找到一个距离最短的值，假设最短的值的节点为j
//每次从 「未求出最短路径的点」中 取出 距离距离起点 最小路径的点，并把这个最短路径的点标记
//4.遍历从i节点后继的所有节点，更新节点，例如i节点后面是j，如果dist[j] > dist[i] + w
//w：i到j的边的距离，那么就更新dist[j] = dist[i] + w;//1 3 4，1 3 4，1 3 4，重复循环完，1步骤是遍历所有节点 
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 510;
int n,m;
int g[N][N],dist[N];//g是邻接矩阵，dist表示起点到当前节点的最短距离，下标就是顶点
//又因为这里我们是带权的，权不一样，所以g二维数组里面的元素表示的是从前一个顶点到这个
//点的边权（距离）,每行每列的下标都代表顶点，元素是边权，边权为0就是两顶点没边
bool st[N];//默认为false，找到这个点的最短路径的话，就标记下来，不用再找了
//算法模板中第一个节点实际上被再次遍历了同时初始化了下一层的所有节点距离
int dijkstra()
{dist[1] = 0;//源点的距离我们默认为1for(int i = 1;i <= n;i++){int t = -1;//因为dijkstra算法不适用于负权边，所以我们用这个判断可以把第一个点//加入for(int j = 1;j <= n;j++)//遍历数组找到从当前顶点直达的最小的路径//为什么可以直接找到直达的，因为我们初始化时，不可达到的距离我们设为正无穷//所以说每次最多能达到初始化过dist的下标，没初始化过的其实就不会去执行t = j了{if(!st[j] && (t == -1 || dist[t] > dist[j]))//后面的或号我们叫短路操作//dist[t] > dist[j]确保了不是直接连通的顶点不会去执行这条语句{t = j;}}st[t] = true;//算法模板中第一个节点实际上被再次遍历了同时初始化了下一层的所有节点距离for(int j = 1;j <=n;j++)//用t去更新最短距离，枚举经过确定t顶点到直达的顶点的距离//并初始化//0x3f3f3f确保了不会执行不是直达的,不过我们还是要遍历n次，可能他由t出发的直达的//边有n条，因为稠密图是假设起点是st那么st的出边可能就有n条边，那么遍历完需要n个起点//稀疏图假设起点是st，出边最多可能有n条边，但是因为n和m相同，所以我们只是o(N){dist[j] = min(dist[j],dist[t] + g[t][j]);}}if(dist[n] == 0x3f3f3f3f) return -1;else return dist[n];
}
int main()
{memset(dist,0x3f,sizeof dist);memset(g,0x3f,sizeof g);cin>>n>>m;for(int i = 0;i < m;i++){int a,b,c;cin>>a>>b>>c;g[a][b] = min(g[a][b],c);}printf("%d",dijkstra());return 0;
}

dijkstra(堆优化版)方法：

class Solution {
public:int h[11100],w[11100],ne[11100],e[11100],idx = 0;int dist[11100];void add(int a,int b,int c){e[idx] = b,ne[idx] = h[a],w[idx] = c,h[a] = idx++;}//st数组保存的是已经被拿来更新过的点//我们每次取的就是，从未被更新过的点集中选出一个离更新过的点的点集(距离点集中的源点最近)最近的点//更新过的点的点集我们记为V,未更新过的点的点集记为Eint st[11000];typedef pair<int,int> PII;priority_queue<PII,vector<PII>,greater<PII>> heap;void dijkstra_heap(int start,int n){dist[start] = 0;heap.push({0,start});while(!heap.empty()){auto t = heap.top();//选出距离源点最小的点，按照dist(距离)排序int dist_u = t.first;int u = t.second;heap.pop();//如果该点是已经之前更新过的点(已经选中去松弛过的点)，那不能被松弛，跳过if(st[u]) continue;else st[u] = 1;for(int i = h[u];i != -1;i = ne[i]){int b = e[i];int c = w[i];if(dist[b] > dist[u] + w[i]){//如果该点被更新了，那么要再加入更新一下dist[b] = dist[u] +w[i];//因为该边被更新了，那么他的邻边也需要更新heap.push({dist[b],b});}}}}int ans[1100];int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {memset(h,-1,sizeof(h));int m = edges.size();for(int i = 0;i < m;i++){int a = edges[i][0];int b = edges[i][1];int c = edges[i][2];add(a,b,c);add(b,a,c);}int min_val = 0x3f3f3f3f;for(int i = 0;i < n;i++){int start = i;memset(dist,0x3f,sizeof(dist));memset(st,0,sizeof(st));dijkstra_heap(start,n);for(int j = 0;j < n;j++){if(j == start) continue;if(dist[j] <= distanceThreshold) ans[start]++;}min_val = min(ans[start],min_val);}cout<<min_val<<endl;int res = -0x3f3f3f3f;for(int i = 0;i < n;i++){if(ans[i] == min_val && res < i) res = i;}return res;}
};

模板题：

#include <iostream>
#include <cstring>
#include <queue>
#include <vector>
using namespace std;
typedef pair<int,int> pll;
const int N = 200010;
int h[N],e[N],ne[N],idx;
int n,m,w[N],dist[N];
bool st[N];
void add(int a,int b,int c)
{e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx++;
}
int dijkstra_2()
{dist[1] = 0;//初始话为0priority_queue<pll,vector<pll>,greater<pll>> heap;//加入第一个heap.push({0,1});//左边是顶点，右边是起点到当前顶点的距离while(!heap.empty()){auto t =heap.top();//大根堆，拿出最小的heap.pop();int k = t.second,dis = t.first;//k代表当前顶点if(st[k]) continue;//如果枚举过了就不用在枚举了st[k] = true;//for(int i = h[k];i != - 1;i = ne[i])//枚举当前最短距离的顶点，找到最小的边，加入{int j = e[i];//找到当前顶点直达的顶点if(dist[j] > dist[k] + w[i])//初始化当前最短的顶点直达的边的距离{dist[j] = dist[k] + w[i];heap.push({dist[j],j});//把顶点和距离加入，优先队列会维护这个队列的}}}if(dist[n] == 0x3f3f3f3f) return 0;else return dist[n];
}
int main()
{cin>>n>>m;memset(h,-1,sizeof h);memset(dist,0x3f,sizeof dist);for(int i = 0;i < m;i++){int a,b,c;cin>>a>>b>>c;add(a,b,c);}if(dijkstra_2() == 0) printf("-1\n");else printf("%d",dijkstra_2());return 0;
}