什么是个人IP?
就是一个人创造出来的属于自己的有个性有价值的,能让他人记住你,信任你,认可你的东西。
如何强化个人IP呢?
需要一些必要的条件如专业性、耐心、勤奋等等要知道,打造IP是一个见效慢的过程,所以可能短期没有太大效果,但一定要坚持。
本文总结了九个关键步骤,旨在帮助你打造个人ip,这些步骤都是非常实用的,值得收藏。

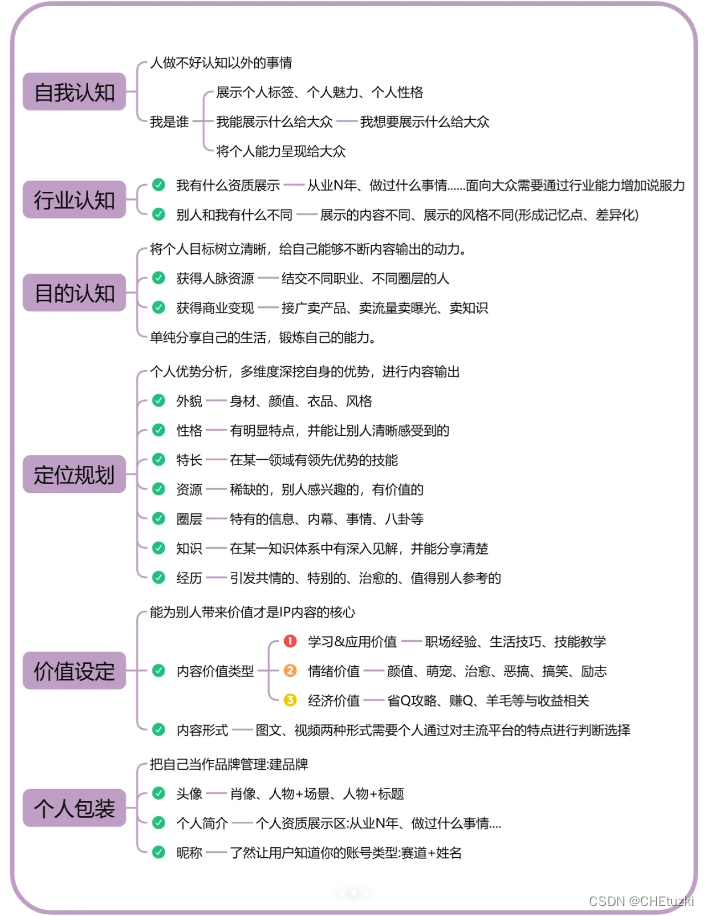
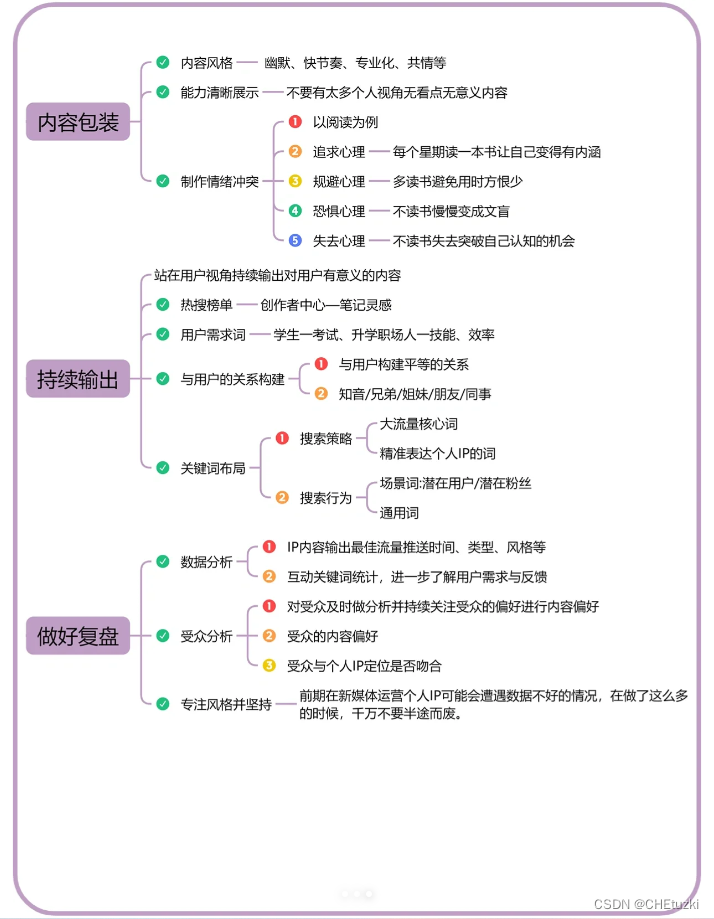
什么是个人IP?
就是一个人创造出来的属于自己的有个性有价值的,能让他人记住你,信任你,认可你的东西。
如何强化个人IP呢?
需要一些必要的条件如专业性、耐心、勤奋等等要知道,打造IP是一个见效慢的过程,所以可能短期没有太大效果,但一定要坚持。
本文总结了九个关键步骤,旨在帮助你打造个人ip,这些步骤都是非常实用的,值得收藏。



本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/178611.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!