前言

  本人作为一名从事了三年演化算法研究的菜鸡研究生，其中大部分时间都在专注于差分演化算法（Differential Evolution, DE）的相关研究。现如今已经毕业，回顾往昔，经过阅读大量的文献，也算是浅浅的入了演化算法的门。
  本文将总结出我在读研期间所收集和阅读过的与 DE 相关的一些论文，以供从事演化算法研究，尤其是 DE 算法研究的各位学者们进行学习和参考。下面我会附上论文的名称和对应的连接，感兴趣的小伙伴可自行下载阅读。
  首先，我们还是先附上 DE 原文:
Storn R, Price K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization, 1997, 11: 341-359.

概述

  在众多的演化算法中，差分演化算法作为一种经典、高效的元启发算法，具有参数少、收敛快、鲁棒性高等优点，使其一度成为了演化计算领域的热点。在2006年至2009年由IEEE举办的CEC演化大赛中，DE连续取得了第一的名次，并且在近三年的竞赛中，DE依旧具有更好的竞争力。DE是由Storn于1995所提出的一种具有较强鲁棒性的优化算法，通过基于种群的随机搜索方式来进行演化更新，每一代的个体都会经历突变、交叉和选择操作，从而将种群不断向全局最优引导。由于其具有较强的鲁棒性和简单性，DE进化已成功地应用于医疗问题优化、工程设计、路径规划、计算机视觉等各种领域中，并取得了显著的效果。
  虽然DE存在许多的优点且受到了广泛的使用，但是该算法依旧存在较多的问题和提升空间，如较多的参数设置、演化寻优的随机性较大、种群多样性的丧失、算法易陷入局部最优、算法早熟、搜索停滞等现象。此类问题的出现会降低DE的算法性能，在解决实际优化问题时会造成不同程度的影响。所以，受到实际问题的驱动，对DE算法的改进和优化从未停止，众多研究者对DE存在的问题进行了讨论及优化。现如今，已有大量的DE变体被提出，极大程度的提高了算法的性能。

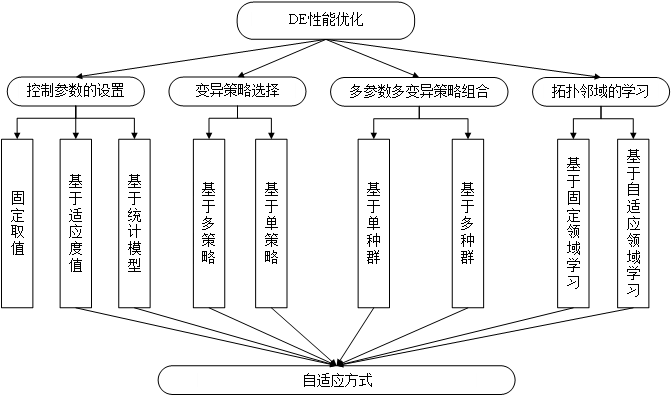
文献综述

1. Brest J, Greiner S, Boskovic B, et al. Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems[J]. IEEE transactions on evolutionary computation, 2006, 10(6): 646-657.
2. Qin A K, Huang V L, Suganthan P N. Differential evolution algorithm with strategy adaptation for global numerical optimization[J]. IEEE transactions on Evolutionary Computation, 2008, 13(2): 398-417.
3. Fan Q, Wang W, Yan X. Differential evolution algorithm with strategy adaptation and knowledge-based control parameters[J]. Artificial Intelligence Review, 2019, 51: 219-253.
4. Wang Y, Cai Z, Zhang Q. Differential evolution with composite trial vector generation strategies and control parameters[J]. IEEE transactions on evolutionary computation, 2011, 15(1): 55-66.
5. Zhang J, Sanderson A C. JADE: adaptive differential evolution with optional external archive[J]. IEEE Transactions on evolutionary computation, 2009, 13(5): 945-958.
6. Mallipeddi R, Suganthan P N, Pan Q K, et al. Differential evolution algorithm with ensemble of parameters and mutation strategies[J]. Applied soft computing, 2011, 11(2): 1679-1696.
7. Mallipeddi R, Suganthan P N. Differential evolution algorithm with ensemble of parameters and mutation and crossover strategies[C]//Swarm, Evolutionary, and Memetic Computing: First International Conference on Swarm, Evolutionary, and Memetic Computing, SEMCCO 2010, Chennai, India, December 16-18, 2010. Proceedings 1. Springer Berlin Heidelberg, 2010: 71-78.
8. Wu G, Mallipeddi R, Suganthan P N, et al. Differential evolution with multi-population based ensemble of mutation strategies[J]. Information Sciences, 2016, 329: 329-345.
9. Tanabe R, Fukunaga A. Success-history based parameter adaptation for differential evolution[C]//2013 IEEE congress on evolutionary computation. IEEE, 2013: 71-78.
10. Li X, Wang L, Jiang Q, et al. Differential evolution algorithm with multi-population cooperation and multi-strategy integration[J]. Neurocomputing, 2021, 421: 285-302.
11. Das S, Mullick S S, Suganthan P N. Recent advances in differential evolution–an updated survey[J]. Swarm and evolutionary computation, 2016, 27: 1-30.
12. Hassan S, Hemeida A M, Alkhalaf S, et al. Multi-variant differential evolution algorithm for feature selection[J]. Scientific Reports, 2020, 10(1): 17261.
13. Ahandani M A. Opposition-based learning in the shuffled bidirectional differential evolution algorithm[J]. Swarm and Evolutionary Computation, 2016, 26: 64-85.
14. Liu X F, Zhan Z H, Lin Y, et al. Historical and heuristic-based adaptive differential evolution[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 49(12): 2623-2635.
15. Ortiz M L, Xiong N. Using random local search helps in avoiding local optimum in differential evolution[C]//Proc. IASTED. 2014: 413-420.
16. Fan Q, Yan X. Self-adaptive differential evolution algorithm with zoning evolution of control parameters and adaptive mutation strategies[J]. IEEE transactions on cybernetics, 2015, 46(1): 219-232.
17. Tian M, Gao X, Dai C. Differential evolution with improved individual-based parameter setting and selection strategy[J]. Applied Soft Computing, 2017, 56: 286-297.
18. Gong W, Cai Z, Liang D. Adaptive ranking mutation operator based differential evolution for constrained optimization[J]. IEEE transactions on cybernetics, 2014, 45(4): 716-727.
19. Tanabe R, Fukunaga A S. Improving the search performance of SHADE using linear population size reduction[C]//2014 IEEE congress on evolutionary computation (CEC). IEEE, 2014: 1658-1665.
20. ZDT D T. Performance analysis of variants of differential evolution on multi-objective optimization problems[J]. Indian Journal of Science and Technology, 2015, 8(17): 65727.
21. Peng H, Guo Z, Deng C, et al. Enhancing differential evolution with random neighbors based strategy[J]. Journal of Computational Science, 2018, 26: 501-511.
22. Yu W J, Shen M, Chen W N, et al. Differential evolution with two-level parameter adaptation[J]. IEEE Transactions on Cybernetics, 2013, 44(7): 1080-1099.
23. Wang Y, Li H X, Huang T, et al. Differential evolution based on covariance matrix learning and bimodal distribution parameter setting[J]. Applied Soft Computing, 2014, 18: 232-247.
24. Xia X, Tong L, Zhang Y, et al. NFDDE: A novelty-hybrid-fitness driving differential evolution algorithm[J]. Information Sciences, 2021, 579: 33-54.
25. Brest J. Constrained real-parameter optimization with ε-self-adaptive differential evolution[M]. Springer Berlin Heidelberg, 2009.
26. Huynh T N, Do D T T, Lee J. Q-Learning-based parameter control in differential evolution for structural optimization[J]. Applied Soft Computing, 2021, 107: 107464.
27. Meng Z, Yang C. Hip-DE: Historical population based mutation strategy in differential evolution with parameter adaptive mechanism[J]. Information Sciences, 2021, 562: 44-77.
28. Li S, Gu Q, Gong W, et al. An enhanced adaptive differential evolution algorithm for parameter extraction of photovoltaic models[J]. Energy Conversion and Management, 2020, 205: 112443.
29. Hao Q, Zhou Z, Wei Z, et al. Parameters identification of photovoltaic models using a multi-strategy success-history-based adaptive differential evolution[J]. IEEE Access, 2020, 8: 35979-35994.
30. Huang Q, Zhang K, Song J, et al. Adaptive differential evolution with a Lagrange interpolation argument algorithm[J]. Information Sciences, 2019, 472: 180-202.
31. Gong W, Cai Z, Ling C X, et al. Enhanced differential evolution with adaptive strategies for numerical optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2010, 41(2): 397-413.
32. Qian W, Chai J, Xu Z, et al. Differential evolution algorithm with multiple mutation strategies based on roulette wheel selection[J]. Applied Intelligence, 2018, 48: 3612-3629.
33. Liu Z Z, Wang Y, Yang S, et al. Differential evolution with a two-stage optimization mechanism for numerical optimization[C]//2016 IEEE congress on evolutionary computation (CEC). IEEE, 2016: 3170-3177.
34. Wang Y, Yu J, Yang S, et al. Evolutionary dynamic constrained optimization: Test suite construction and algorithm comparisons[J]. Swarm and Evolutionary Computation, 2019, 50: 100559.
35. Li Y, Wang S, Liu H, et al. A backtracking differential evolution with multi-mutation strategies autonomy and collaboration[J]. Applied Intelligence, 2022: 1-27.
36. Ali I M, Essam D, Kasmarik K. Novel binary differential evolution algorithm for knapsack problems[J]. Information Sciences, 2021, 542: 177-194.
37. Xie W, Yu W, Zou X. Diversity-maintained differential evolution embedded with gradient-based local search[J]. Soft computing, 2013, 17: 1511-1535.
38. Peng H, Wu Z. Heterozygous differential evolution with Taguchi local search[J]. Soft Computing, 2015, 19: 3273-3291.
39. Liao J, Cai Y, Wang T, et al. Cellular direction information based differential evolution for numerical optimization: an empirical study[J]. Soft Computing, 2016, 20: 2801-2827.
40. Kaelo P, Ali M M. A numerical study of some modified differential evolution algorithms[J]. European journal of operational research, 2006, 169(3): 1176-1184.
41. Brest J, Maučec M S, Bošković B. Single objective real-parameter optimization: Algorithm jSO[C]//2017 IEEE congress on evolutionary computation (CEC). IEEE, 2017: 1311-1318.
42. Tan Z, Li K, Wang Y. Differential evolution with adaptive mutation strategy based on fitness landscape analysis[J]. Information Sciences, 2021, 549: 142-163.
43. Zuo Y, Zhao F, Li Z. A knowledge-based differential covariance matrix adaptation cooperative algorithm[J]. Expert Systems with Applications, 2021, 184: 115495.
44. Zeng Z, Zhang M, Chen T, et al. A new selection operator for differential evolution algorithm[J]. Knowledge-Based Systems, 2021, 226: 107150.
45. Lu Z, Zhang L, Wang D. Differential evolution with improved elite archive mutation and dynamic parameter adjustment[J]. Cluster Computing, 2019, 22: 9347-9356.
46. Zhang X, Zhang X. Improving differential evolution by differential vector archive and hybrid repair method for global optimization[J]. Soft Computing, 2017, 21: 7107-7116.
47. Das S, Konar A, Chakraborty U K. Two improved differential evolution schemes for faster global search[C]//Proceedings of the 7th annual conference on Genetic and evolutionary computation. 2005: 991-998.
48. Yang Z, Yao X, He J. Making a difference to differential evolution[J]. Advances in metaheuristics for hard optimization, 2008: 397-414.
49. Das S, Konar A, Chakraborty U K. Two improved differential evolution schemes for faster global search[C]//Proceedings of the 7th annual conference on Genetic and evolutionary computation. 2005: 991-998.
50. Liang J, Qiao K, Yu K, et al. Parameters estimation of solar photovoltaic models via a self-adaptive ensemble-based differential evolution[J]. Solar Energy, 2020, 207: 336-346.
51. Cui L, Huang Q, Li G, et al. Differential evolution algorithm with tracking mechanism and backtracking mechanism[J]. IEEE Access, 2018, 6: 44252-44267.
52. Meng Z, Chen Y, Li X. Enhancing differential evolution with novel parameter control[J]. IEEE Access, 2020, 8: 51145-51167.
53. Zou D, Gong D. Differential evolution based on migrating variables for the combined heat and power dynamic economic dispatch[J]. Energy, 2022, 238: 121664.
54. Zhou X G, Zhang G J, Hao X H, et al. Differential evolution with multi-stage strategies for global optimization[C]//2016 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2016: 2550-2557.
55. Mohamed A K, Mohamed A W. Real-parameter unconstrained optimization based on enhanced AGDE algorithm[J]. Machine learning paradigms: Theory and application, 2019: 431-450.
56. Cui L, Li G, Zhu Z, et al. Adaptive multiple-elites-guided composite differential evolution algorithm with a shift mechanism[J]. Information Sciences, 2018, 422: 122-143.
57. Kizilay D, Tasgetiren M F, Oztop H, et al. A differential evolution algorithm with q-learning for solving engineering design problems[C]//2020 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2020: 1-8.
58. Sharma M, Komninos A, López-Ibáñez M, et al. Deep reinforcement learning based parameter control in differential evolution[C]//Proceedings of the Genetic and Evolutionary Computation Conference. 2019: 709-717.
59. Tan Z, Li K. Differential evolution with mixed mutation strategy based on deep reinforcement learning[J]. Applied Soft Computing, 2021, 111: 107678.
60. Zhang H, Sun J, Xu Z. Learning to mutate for differential evolution[C]//2021 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2021: 1-8.
61. El-Qulity S A, Mohamed A W. A generalized national planning approach for admission capacity in higher education: a nonlinear integer goal programming model with a novel differential evolution algorithm[J]. Computational Intelligence and Neuroscience, 2016, 2016: 21-21.
62. Mohamed A W. An improved differential evolution algorithm with triangular mutation for global numerical optimization[J]. Computers & Industrial Engineering, 2015, 85: 359-375.
63. Mohamed A W, Mohamed A K. Adaptive guided differential evolution algorithm with novel mutation for numerical optimization[J]. International Journal of Machine Learning and Cybernetics, 2019, 10: 253-277.
64. Wu G, Shen X, Li H, et al. Ensemble of differential evolution variants[J]. Information Sciences, 2018, 423: 172-186.
65. Mohamed A W, Hadi A A, Jambi K M. Novel mutation strategy for enhancing SHADE and LSHADE algorithms for global numerical optimization[J]. Swarm and Evolutionary Computation, 2019, 50: 100455.
66. Mohamed A W, Hadi A A, Mohamed A K. Differential evolution mutations: taxonomy, comparison and convergence analysis[J]. IEEE Access, 2021, 9: 68629-68662.
67. Mohamed A W, Hadi A A, Fattouh A M, et al. LSHADE with semi-parameter adaptation hybrid with CMA-ES for solving CEC 2017 benchmark problems[C]//2017 IEEE Congress on evolutionary computation (CEC). IEEE, 2017: 145-152.
68. Kumar A, Misra R K, Singh D. Improving the local search capability of effective butterfly optimizer using covariance matrix adapted retreat phase[C]//2017 IEEE congress on evolutionary computation (CEC). IEEE, 2017: 1835-1842.
69. Kudela J, Matousek R. Lipschitz-based surrogate model for high-dimensional computationally expensive problems[J]. arXiv preprint arXiv:2204.14236, 2022.
70. Cui L, Huang Q, Li G, et al. Differential evolution algorithm with tracking mechanism and backtracking mechanism[J]. IEEE Access, 2018, 6: 44252-44267.
71. Meng Z, Zhong Y, Yang C. CS-DE: Cooperative strategy based differential evolution with population diversity enhancement[J]. Information Sciences, 2021, 577: 663-696.
72. Meng Z, Yang C. Hip-DE: Historical population based mutation strategy in differential evolution with parameter adaptive mechanism[J]. Information Sciences, 2021, 562: 44-77.
73. Meng Z, Yang C, Li X, et al. Di-DE: depth information-based differential evolution with adaptive parameter control for numerical optimization[J]. IEEE Access, 2020, 8: 40809-40827.
74. Biswas S, Saha D, De S, et al. Improving differential evolution through Bayesian hyperparameter optimization[C]//2021 IEEE Congress on evolutionary computation (CEC). IEEE, 2021: 832-840.
75. Cui L, Li G, Lin Q, et al. Adaptive differential evolution algorithm with novel mutation strategies in multiple sub-populations[J]. Computers & Operations Research, 2016, 67: 155-173.
76. Ge Y F, Yu W J, Lin Y, et al. Distributed differential evolution based on adaptive mergence and split for large-scale optimization[J]. IEEE transactions on cybernetics, 2017, 48(7): 2166-2180.
77. Tan Z, Tang Y, Li K, et al. Differential evolution with hybrid parameters and mutation strategies based on reinforcement learning[J]. Swarm and Evolutionary Computation, 2022, 75: 101194.
78. Gui L, Xia X, Yu F, et al. A multi-role based differential evolution[J]. Swarm and Evolutionary Computation, 2019, 50: 100508.
79. Cao Z, Jia H, Wang Z, et al. A differential evolution with autonomous strategy selection and its application in remote sensing image denoising[J]. Expert Systems with Applications, 2023: 122108.
80. Li C, Sun G, Deng L, et al. A population state evaluation-based improvement framework for differential evolution[J]. Information Sciences, 2023, 629: 15-38.
81. Li Y, Wang S, Yang B, et al. Population reduction with individual similarity for differential evolution[J]. Artificial Intelligence Review, 2023, 56(5): 3887-3949.
82. Ahmad M F, Isa N A M, Lim W H, et al. Differential evolution: A recent review based on state-of-the-art works[J]. Alexandria Engineering Journal, 2022, 61(5): 3831-3872.
83. Song Y, Cai X, Zhou X, et al. Dynamic hybrid mechanism-based differential evolution algorithm and its application[J]. Expert Systems with Applications, 2023, 213: 118834.
84. Wang M, Ma Y, Wang P. Parameter and strategy adaptive differential evolution algorithm based on accompanying evolution[J]. Information Sciences, 2022, 607: 1136-1157.
85. Meng Z, Yang C. Two-stage differential evolution with novel parameter control[J]. Information Sciences, 2022, 596: 321-342.
86. Piotrowski A P, Napiorkowski J J, Piotrowska A E. Particle swarm optimization or differential evolution—A comparison[J]. Engineering Applications of Artificial Intelligence, 2023, 121: 106008.
87. Zhang S X, Wen Y N, Liu Y H, et al. Differential evolution with domain transform[J]. IEEE Transactions on Evolutionary Computation, 2022.
88. Qiao K, Liang J, Yu K, et al. Self-adaptive resources allocation-based differential evolution for constrained evolutionary optimization[J]. Knowledge-Based Systems, 2022, 235: 107653.
89. Qiao K, Liang J, Qu B, et al. Differential evolution with level-based learning mechanism[J]. Complex System Modeling and Simulation, 2022, 2(1): 35-58.
90. Cao Z, Wang Z, Fu Y, et al. An adaptive differential evolution framework based on population feature information[J]. Information Sciences, 2022, 608: 1416-1440.
91. Song Y, Zhao G, Zhang B, et al. An enhanced distributed differential evolution algorithm for portfolio optimization problems[J]. Engineering Applications of Artificial Intelligence, 2023, 121: 106004.
92. Li Y, Han T, Tang S, et al. An improved differential evolution by hybridizing with estimation-of-distribution algorithm[J]. Information Sciences, 2023, 619: 439-456.
93. Zeng Z, Zhang M, Hong Z, et al. Enhancing differential evolution with a target vector replacement strategy[J]. Computer Standards & Interfaces, 2022, 82: 103631.
94. Zeng Z, Hong Z, Zhang H, et al. Improving differential evolution using a best discarded vector selection strategy[J]. Information Sciences, 2022, 609: 353-375.
95. Vermetten D, van Stein B, Kononova A V, et al. Analysis of structural bias in differential evolution configurations[M]//Differential Evolution: From Theory to Practice. Singapore: Springer Nature Singapore, 2022: 1-22.
96. Kitamura T, Fukunaga A. Differential Evolution with an Unbounded Population[C]//2022 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2022: 1-8.
97. Gupta S, Su R. An efficient differential evolution with fitness-based dynamic mutation strategy and control parameters[J]. Knowledge-Based Systems, 2022, 251: 109280.
98. Deng W, Ni H, Liu Y, et al. An adaptive differential evolution algorithm based on belief space and generalized opposition-based learning for resource allocation[J]. Applied Soft Computing, 2022, 127: 109419.
99. Li Y, Wang S, Yang H, et al. Enhancing differential evolution algorithm using leader-adjoint populations[J]. Information Sciences, 2023, 622: 235-268.
100. Chen J, Wang R, Wu D, et al. A differential evolution-enhanced position-transitional approach to latent factor analysis[J]. IEEE Transactions on Emerging Topics in Computational Intelligence, 2022, 7(2): 389-401.

总结

  有关 DE 的相关论文不计其数，这里小编也不可能一一的列出。但是希望从事 DE 相关研究的学者能够不断的集思广益，多汲取一些大佬的思想，能够在算法优化上更上一层楼。
  我将收集到的一些论文进行了打包上传，链接如下：差分演化算法相关学术论文集合