这一节中我们将学习向量空间。
x.1 转置矩阵和构造对称矩阵
在开启向量空间的学习前我们先复习一下转置矩阵和置换矩阵。我们将矩阵转置前后不变的矩阵称为对称矩阵。而我们如何得到一个对称矩阵呢,我们使用矩阵乘以矩阵的转置便可得到。
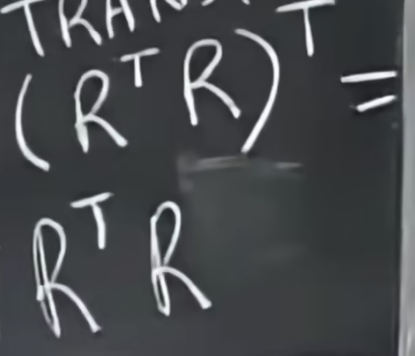
x.2 Vectors Space
向量空间必须对数乘和相加运算封闭,即满足线性组合。
对于R2的空间而言的向量子空间,它必须过原点才构成R2的向量子空间。但实际上R2的子空间数量是非常有限的,于是我们将R2的子空间全部列举出来,有:
1)R2平面本身。
2)任何经过[0, 0]T的直线。
3)只包含原点[0, 0]的向量集合。
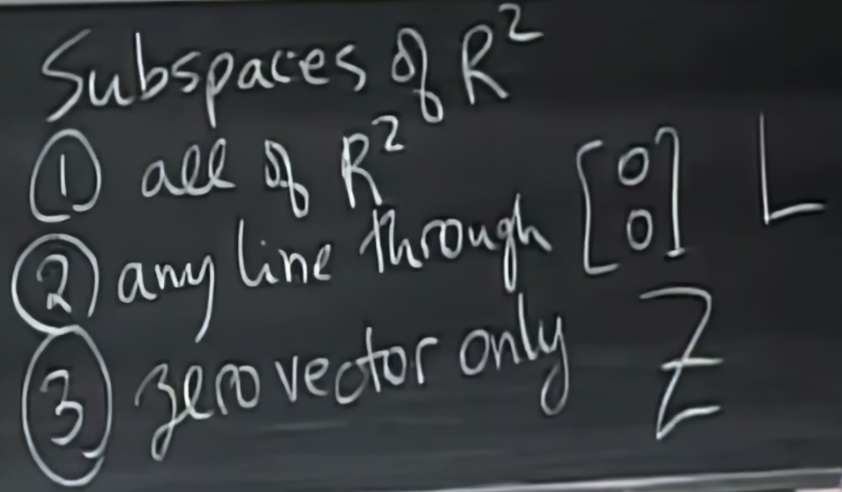
我们将二维的思想推广到三维空间中,寻找三维空间下的向量子空间,易于求得 R 3 R^3 R3向量空间下只有如下四种向量子空间:
1)R3立体本身。
2)经过原点的平面。
3)经过原点的直线。
4)只包含原点[0, 0, 0]的向量集合。
为了更好地理解向量子空间的定义,我们再举一个属于 R 3 R^3 R3的矩阵的例子[[1, 3], [2, 3], [4, 1]]T,对于这个矩阵,我们只观察它的列向量,由列向量构成的向量子空间是一个平面,因为只有在这个平面中,才对其列向量[1, 2, 4]T和[3, 3, 1]T的数乘和加法都封闭。这个向量子空间也叫作列空间。