题目
695. 岛屿的最大面积
中等
相关标签
深度优先搜索 广度优先搜索 并查集 数组 矩阵
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
示例 1:
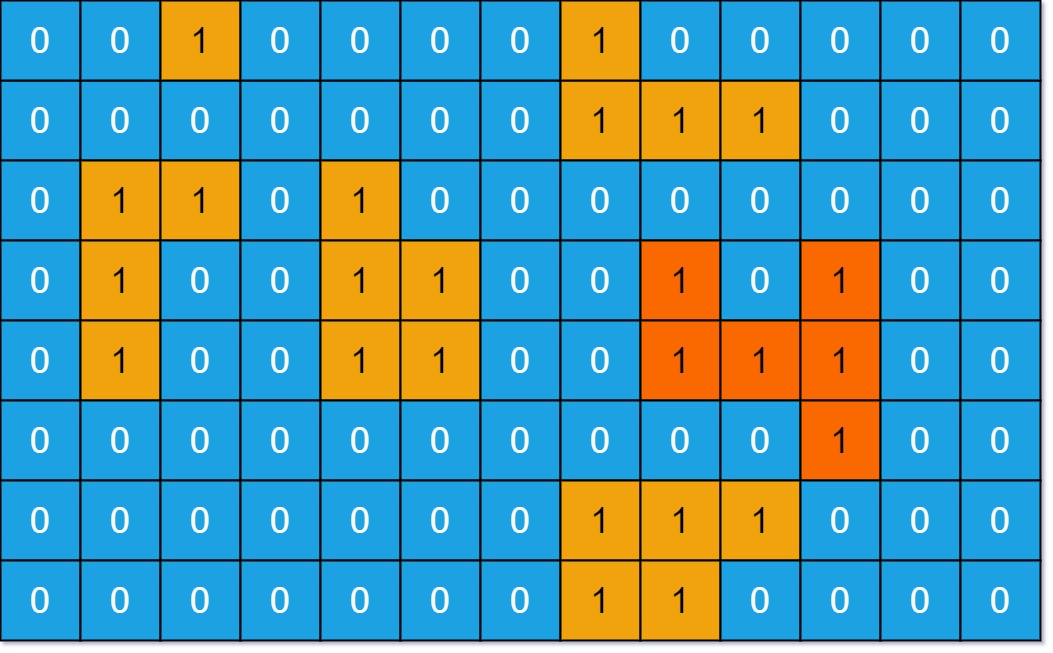
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] 输出:6 解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1。
示例 2:
输入:grid = [[0,0,0,0,0,0,0,0]] 输出:0
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 50grid[i][j]为0或1
思路和解题方法 1 DFS
dfs函数通过传入的坐标(x, y)来探索当前陆地区域的情况。如果当前坐标越界(超出了网格范围)或者是海洋(值为 0),则返回面积 0,表示此处不是陆地。如果当前坐标是陆地(值为 1),则将其标记为已访问过(即将值置为 0),以免重复访问同一块陆地。然后开始向当前位置的上、下、左、右四个方向进行深度优先搜索,探索与当前陆地相连的其他陆地。
在每一步深度优先搜索中,我们累加当前陆地的面积,并递归地探索相邻的陆地。这样,通过深度优先搜索,我们能够计算出以当前位置为起点的整个连通陆地区域的面积。
最后,将累计的面积作为返回值返回给上一级递归调用。
在
maxAreaOfIsland函数中,我们遍历整个网格,对于每个岛屿的起始位置(即值为 1 的位置),调用dfs函数来计算以该位置为起点的岛屿的面积。并将得到的面积与当前记录的最大面积进行比较,并更新最大面积的值。
时间复杂度分析:
- 对于每个格子,最坏情况下需要进行深度优先搜索,而深度优先搜索的时间复杂度是 O(m*n),其中 m 和 n 分别为 grid 的行数和列数。
- 因此,总的时间复杂度为 O(m*n),其中 m 为 grid 的行数,n 为 grid 的列数。
空间复杂度分析:
- 深度优先搜索过程中使用的递归调用栈的最大深度为岛屿的大小,最坏情况下为整个 grid 大小,因此空间复杂度为 O(m*n)。
- 此外,还需要考虑输入参数和一些辅助变量的空间占用,但是这些空间占用都是常数级别的,因此不影响总体的空间复杂度。
综上所述,该算法的时间复杂度为 O(mn),空间复杂度也为 O(mn)。
c++ 代码
class Solution {
public:// 深度优先搜索函数,用于搜索连通的岛屿区域并返回面积int dfs(vector<vector<int>>& grid, int x, int y) {// 递归终止条件if (x < 0 || x == grid.size() || y < 0 || y == grid[0].size() || grid[x][y] == 0) return 0;grid[x][y] = 0; // 将已经搜索过的陆地置为0,防止重复搜索(即将其视为沉没的岛屿)int ans = 1;// 分别搜索当前陆地的上、下、右、左四个方向的区块ans += dfs(grid, x, y + 1); // 上面ans += dfs(grid, x, y - 1); // 下面ans += dfs(grid, x + 1, y); // 右边ans += dfs(grid, x - 1, y); // 左边return ans; // 返回当前连通岛屿的总面积}// 计算最大岛屿面积的函数int maxAreaOfIsland(vector<vector<int>>& grid) {int ans = 0; // 初始化最大面积为0for (int i = 0; i != grid.size(); ++i) {for (int j = 0; j != grid[0].size(); ++j) {if (grid[i][j] == 1) { // 如果当前位置是陆地int cnt = dfs(grid, i, j); // 对当前的岛屿区域进行深度优先搜索,得到面积ans = max(ans, cnt); // 更新最大面积}}}return ans; // 返回最大岛屿面积}
};
思路和解题方法 2 BFS
首先,定义了一个类
Solution,其中包含了一个公有函数maxAreaOfIsland,该函数接收一个二维向量grid作为参数,并返回岛屿的最大面积。在
maxAreaOfIsland函数中,我们首先初始化ans为 0,以便记录最大的岛屿面积。接下来是两个嵌套的
for循环,用来遍历整个二维网格grid。在每次迭代中,我们首先初始化
cur为 0,用于记录当前岛屿的面积。然后创建两个队列queuei和queuej,用于存储待访问的陆地坐标。将当前遍历到的位置
(i, j)入队,即将它们分别加入到queuei和queuej中。进入while循环,只要队列非空,就不断进行以下操作:
- 弹出队首的坐标
(cur_i, cur_j);- 检查当前坐标是否越界或者不是陆地,若是则跳过本次循环;
- 若当前坐标是陆地,则将当前面积
cur自增,并将当前坐标标记为已访问过的海洋(即将值置为 0),然后探索当前位置的上、下、左、右四个方向;- 将相邻的陆地坐标入队。
在每次内部循环结束时,更新
ans为当前cur和ans之间的较大值。最后,遍历结束后返回
ans,即为岛屿的最大面积。
时间复杂度分析:
时间复杂度取决于岛屿的数量和网格的大小。假设网格的行数为 m,列数为 n,岛屿的数量为 k,那么时间复杂度可以表示为 O(mn+k),其中 mn 表示遍历整个网格的时间复杂度,k 表示计算岛屿面积的时间复杂度。
空间复杂度分析:
- 空间复杂度方面,使用了两个队列
queuei和queuej,它们的最大长度可以达到网格的面积大小,因此空间复杂度也是 O(m*n)。
综上所述,该算法的时间复杂度为 O(mn),空间复杂度也为 O(mn)。
c++ 代码
class Solution {
public:int maxAreaOfIsland(vector<vector<int>>& grid) {int ans = 0;// 遍历二维网格的每一个位置for (int i = 0; i != grid.size(); ++i) {for (int j = 0; j != grid[0].size(); ++j) {int cur = 0; // 当前岛屿的面积queue<int> queuei;queue<int> queuej;queuei.push(i); // 将当前位置加入队列queuej.push(j);while (!queuei.empty()) {int cur_i = queuei.front(), cur_j = queuej.front(); // 取出队首元素queuei.pop();queuej.pop();if (cur_i < 0 || cur_j < 0 || cur_i == grid.size() || cur_j == grid[0].size() || grid[cur_i][cur_j] != 1) {continue; // 如果当前位置超出边界或者不是岛屿,跳过}++cur; // 当前岛屿面积加一grid[cur_i][cur_j] = 0; // 将当前位置置为0,表示已经访问过int di[4] = {0, 0, 1, -1}; // 方向数组,表示上下左右四个方向int dj[4] = {1, -1, 0, 0};for (int index = 0; index != 4; ++index) {int next_i = cur_i + di[index], next_j = cur_j + dj[index]; // 计算四个相邻位置queuei.push(next_i); // 将相邻位置加入队列queuej.push(next_j);}}ans = max(ans, cur); // 更新最大岛屿面积}}return ans; // 返回最大岛屿面积}
};
附Java代码
DFS
class Solution {public int maxAreaOfIsland(int[][] grid) {int ans = 0; // 初始化最大岛屿面积为0for (int i = 0; i != grid.length; ++i) { // 遍历二维网格的每一个位置for (int j = 0; j != grid[0].length; ++j) {ans = Math.max(ans, dfs(grid, i, j)); // 计算以当前位置为起点的岛屿面积,并更新最大值}}return ans; // 返回最大岛屿面积}public int dfs(int[][] grid, int cur_i, int cur_j) {if (cur_i < 0 || cur_j < 0 || cur_i == grid.length || cur_j == grid[0].length || grid[cur_i][cur_j] != 1) {return 0; // 如果当前位置超出边界或者不是岛屿,返回面积为0}grid[cur_i][cur_j] = 0; // 将当前位置置为0,表示已经访问过int[] di = {0, 0, 1, -1}; // 方向数组,表示上下左右四个方向int[] dj = {1, -1, 0, 0};int ans = 1; // 当前岛屿面积初始化为1for (int index = 0; index != 4; ++index) {int next_i = cur_i + di[index], next_j = cur_j + dj[index]; // 计算四个相邻位置ans += dfs(grid, next_i, next_j); // 递归计算相邻位置的岛屿面积并累加}return ans; // 返回当前岛屿面积}
}
BFS
class Solution {// 计算岛屿的最大面积public int maxAreaOfIsland(int[][] grid) {int ans = 0; // 初始化最大面积为 0// 遍历整个网格for (int i = 0; i != grid.length; ++i) {for (int j = 0; j != grid[0].length; ++j) {int cur = 0; // 当前岛屿的面积Queue<Integer> queuei = new LinkedList<Integer>(); // 存储陆地坐标的队列Queue<Integer> queuej = new LinkedList<Integer>(); // 存储陆地坐标的队列queuei.offer(i); // 将当前坐标入队queuej.offer(j); // 将当前坐标入队// BFS 遍历岛屿while (!queuei.isEmpty()) {int cur_i = queuei.poll(), cur_j = queuej.poll(); // 出队当前坐标// 检查当前坐标是否越界或者不是陆地,若是则跳过本次循环if (cur_i < 0 || cur_j < 0 || cur_i == grid.length || cur_j == grid[0].length || grid[cur_i][cur_j] != 1) {continue;}++cur; // 当前岛屿的面积加一grid[cur_i][cur_j] = 0; // 标记当前坐标为已访问过的海洋int[] di = {0, 0, 1, -1}; // 方向数组,分别表示上、下、左、右四个方向int[] dj = {1, -1, 0, 0}; // 方向数组,分别表示上、下、左、右四个方向// 探索当前位置的上、下、左、右四个方向for (int index = 0; index != 4; ++index) {int next_i = cur_i + di[index], next_j = cur_j + dj[index]; // 计算相邻坐标queuei.offer(next_i); // 将相邻的陆地坐标入队queuej.offer(next_j); // 将相邻的陆地坐标入队}}ans = Math.max(ans, cur); // 更新最大面积}}return ans; // 返回岛屿的最大面积}
}
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
![2023年中国骨质疏松治疗仪发展趋势分析:小型且智能将成为产品优化方向[图]](https://img-blog.csdnimg.cn/img_convert/7f219a06f57b91242369de2e5641b5a4.png)