淘宝的“双十一”购物节有各种促销活动，比如“满200元减50元”。假设你女朋友的购物车中有n个（n>100）想买的商品，她希望从里面选几个，在凑够满减条件的前提下，让选出来的商品价格总和最大程度地接近满减条件（200元），这样就可以极大限度地“薅羊毛”。作为程序员的你，能不能编个代码来帮她搞定呢？

要想高效地解决这个问题，就要用到我们今天讲的动态规划（Dynamic Programming）。

动态规划学习路线

动态规划比较适合用来求解最优问题，比如求最大值、最小值等等。它可以非常显著地降低时间复杂度，提高代码的执行效率。不过，它也是出了名的难学。它的主要学习难点跟递归类似，那就是，求解问题的过程不太符合人类常规的思维方式。对于新手来说，要想入门确实不容易。不过，等你掌握了之后，你会发现，实际上并没有想象中那么难。

为了让你更容易理解动态规划，我分了三节给你讲解。这三节分别是，初识动态规划、动态规划理论、动态规划实战。

第一节，我会通过两个非常经典的动态规划问题模型，向你展示我们为什么需要动态规划，以及动态规划解题方法是如何演化出来的。实际上，你只要掌握了这两个例子的解决思路，对于其他很多动态规划问题，你都可以套用类似的思路来解决。

第二节，我会总结动态规划适合解决的问题的特征，以及动态规划解题思路。除此之外，我还会将贪心、分治、回溯、动态规划这四种算法思想放在一起，对比分析它们各自的特点以及适用的场景。

第三节，我会教你应用第二节讲的动态规划理论知识，实战解决三个非常经典的动态规划问题，加深你对理论的理解。弄懂了这三节中的例子，对于动态规划这个知识点，你就算是入门了。

0-1背包问题

我在讲贪心算法、回溯算法的时候，多次讲到背包问题。今天，我们依旧拿这个问题来举例。

对于一组不同重量、不可分割的物品，我们需要选择一些装入背包，在满足背包最大重量限制的前提下，背包中物品总重量的最大值是多少呢？

关于这个问题，我们上一节讲了回溯的解决方法，也就是穷举搜索所有可能的装法，然后找出满足条件的最大值。不过，回溯算法的复杂度比较高，是指数级别的。那有没有什么规律，可以有效降低时间复杂度呢？我们一起来看看。

// 回溯算法实现。注意：我把输入的变量都定义成了成员变量。
private int maxW = Integer.MIN_VALUE; // 结果放到maxW中
private int[] weight = {2，2，4，6，3};  // 物品重量
private int n = 5; // 物品个数
private int w = 9; // 背包承受的最大重量
public void f(int i, int cw) { // 调用f(0, 0)if (cw == w || i == n) { // cw==w表示装满了，i==n表示物品都考察完了if (cw > maxW) maxW = cw;return;}f(i+1, cw); // 选择不装第i个物品if (cw + weight[i] <= w) {f(i+1,cw + weight[i]); // 选择装第i个物品}
}

规律是不是不好找？那我们就举个例子、画个图看看。我们假设背包的最大承载重量是9。我们有5个不同的物品，每个物品的重量分别是2，2，4，6，3。如果我们把这个例子的回溯求解过程，用递归树画出来，就是下面这个样子：

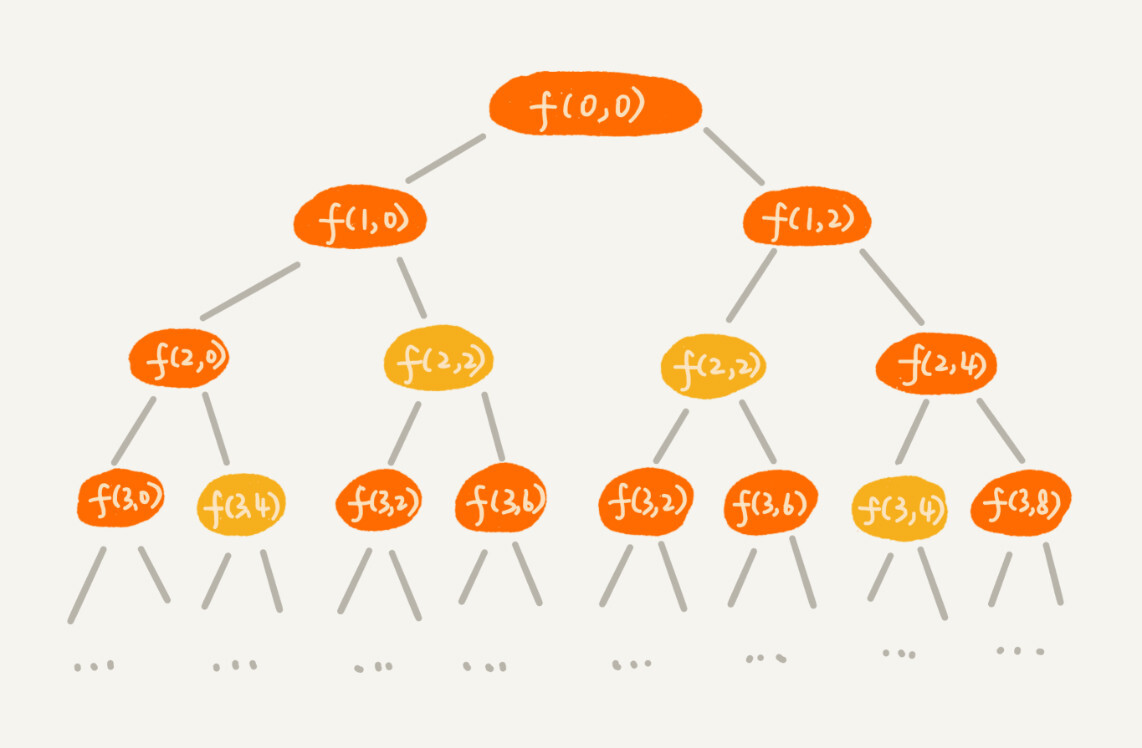
递归树中的每个节点表示一种状态，我们用（i, cw）来表示。其中，i表示将要决策第几个物品是否装入背包，cw表示当前背包中物品的总重量。比如，（2，2）表示我们将要决策第2个物品是否装入背包，在决策前，背包中物品的总重量是2。

从递归树中，你应该能会发现，有些子问题的求解是重复的，比如图中f(2, 2)和f(3,4)都被重复计算了两次。我们可以借助递归那一节讲的“备忘录”的解决方式，记录已经计算好的f(i, cw)，当再次计算到重复的f(i, cw)的时候，可以直接从备忘录中取出来用，就不用再递归计算了，这样就可以避免冗余计算。

private int maxW = Integer.MIN_VALUE; // 结果放到maxW中
private int[] weight = {2，2，4，6，3};  // 物品重量
private int n = 5; // 物品个数
private int w = 9; // 背包承受的最大重量
private boolean[][] mem = new boolean[5][10]; // 备忘录，默认值false
public void f(int i, int cw) { // 调用f(0, 0)if (cw == w || i == n) { // cw==w表示装满了，i==n表示物品都考察完了if (cw > maxW) maxW