1. 题目链接:300. 最长递增子序列
2. 题目描述:
给你一个整数数组
nums,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,
[3,6,2,7]是数组[0,3,1,6,2,2,7]的子序列。示例 1:
输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。示例 2:
输入:nums = [0,1,0,3,2,3] 输出:4示例 3:
输入:nums = [7,7,7,7,7,7,7] 输出:1提示:
1 <= nums.length <= 2500-104 <= nums[i] <= 104
3. 解法1(暴力搜索):
【时间复杂度过高会超时】
3.1 算法思路:
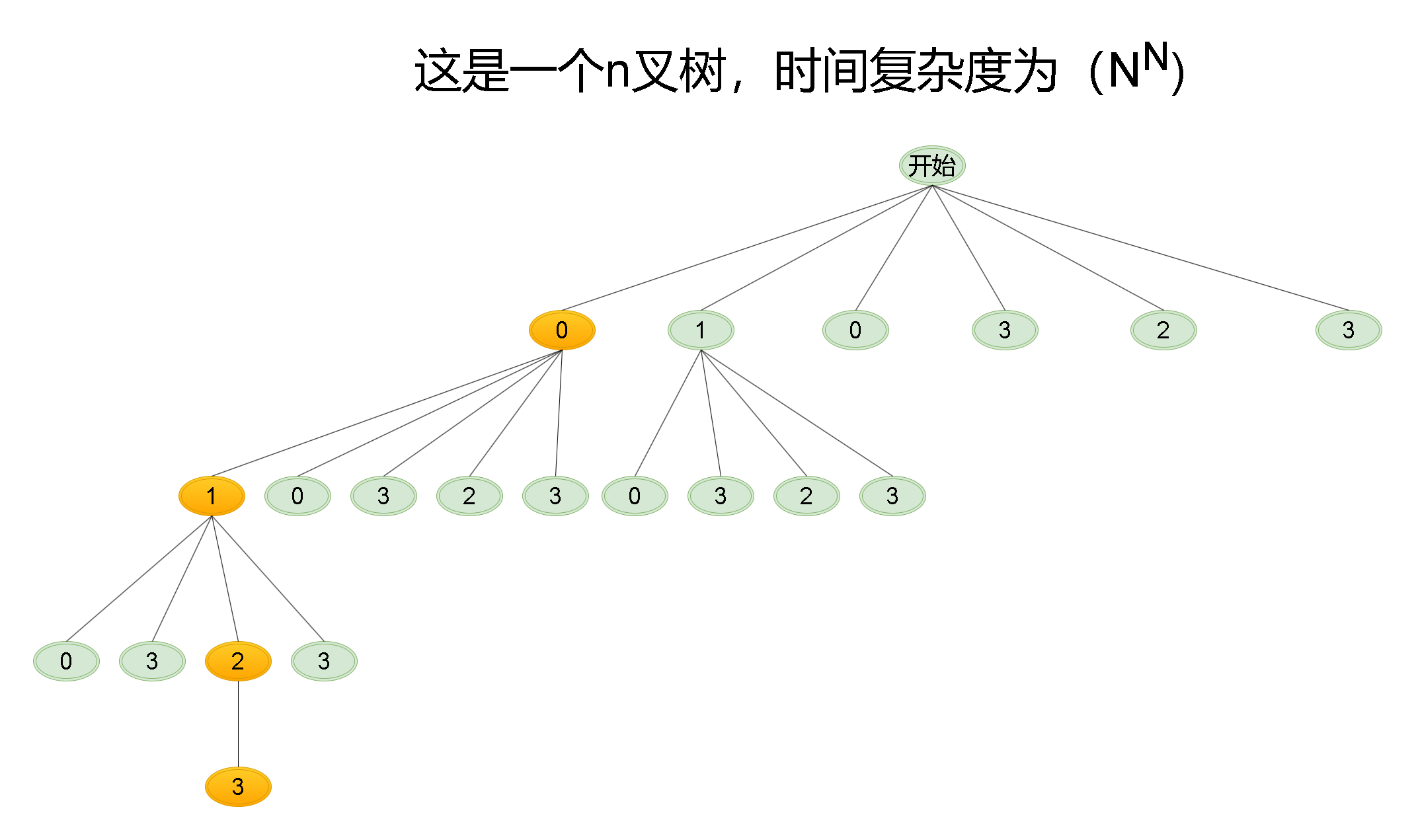
- 递归含义:给
dfs一个使命,给他应该数i,返回以i位置为起点的最长递增序列的长度 - 函数体:遍历
i后面的所有位置,看看谁能加到i这个元素的后面。统计所有情况下的最大值 - 递归出口:因为我们是判断之后再进入递归的,因此没有出口
3.2 C++算法代码:
class Solution {
public:int lengthOfLIS(vector<int>& nums) {int ret=0;for(int i=0;i<nums.size();i++){ret=max(ret,dfs(i,nums));}return ret;}int dfs(int pos,vector<int>&nums){int ret=1;for(int i=pos+1;i<nums.size();i++){if(nums[i]>nums[pos])ret=max(ret,dfs(i,nums)+1);}return ret;}
};
4. 解法2(记忆化搜索):
4.1 算法思路:
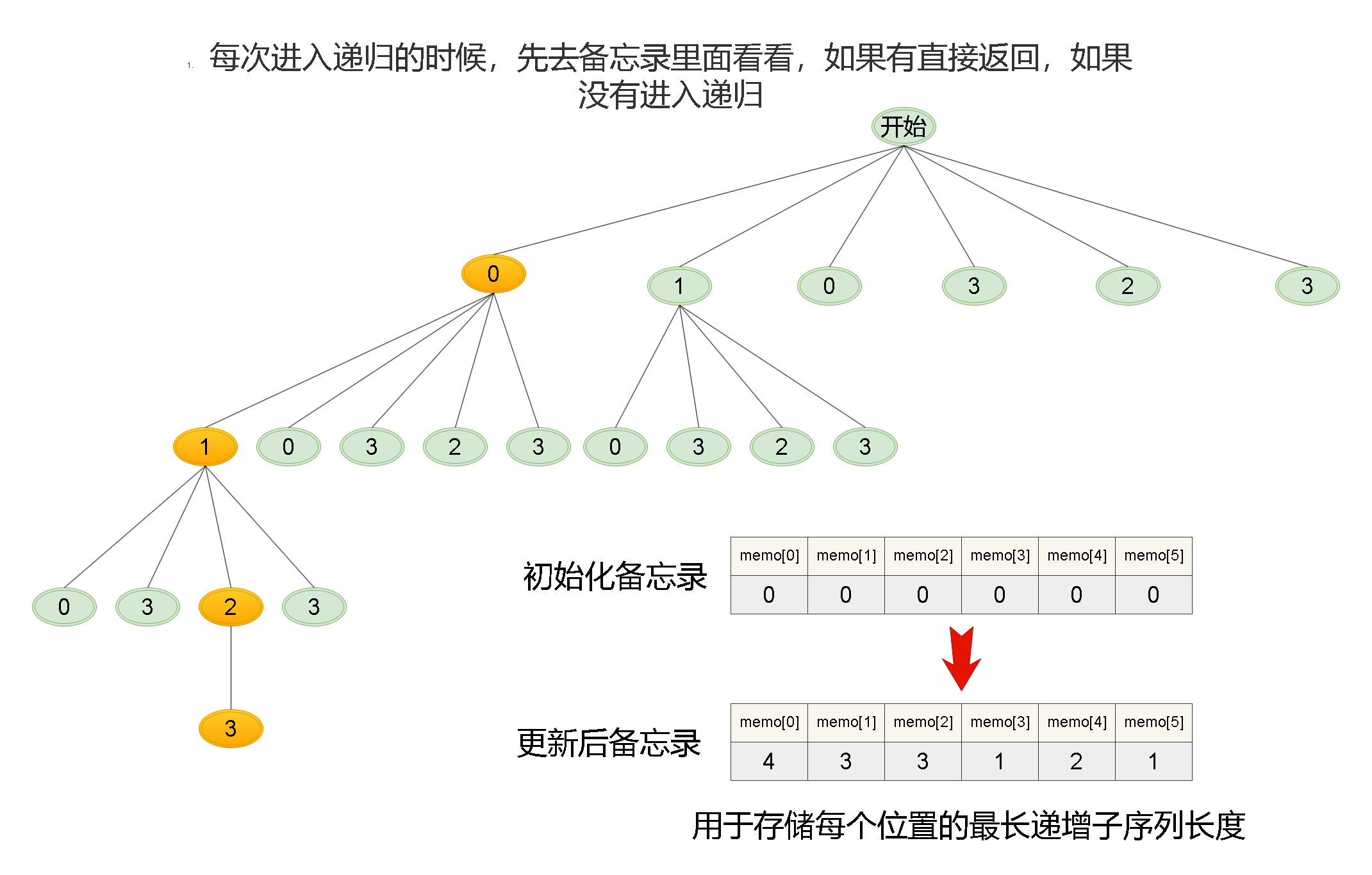
- 加上一个备忘录
- 每次进入递归的时候,去备忘录里面看看
- 每次返回的时候,将结果加入到备忘录里面
4.2 C++算法代码:
class Solution {
public:int lengthOfLIS(vector<int>& nums) {int ret=0; // 初始化最长递增子序列的长度为0int n=nums.size(); // 获取数组长度vector<int> memo(n); // 创建一个与nums长度相同的memo数组,用于存储每个位置的最长递增子序列长度for(int i=0;i<n;i++) // 遍历nums数组{ret=max(ret,dfs(i,nums,memo)); // 更新最长递增子序列的长度}return ret; // 返回最长递增子序列的长度}int dfs(int pos,vector<int>&nums,vector<int>&memo) // 深度优先搜索函数,用于计算以pos位置为结尾的最长递增子序列的长度{if(memo[pos]!=0) return memo[pos]; // 如果memo数组中已经存在以pos位置为结尾的最长递增子序列的长度,则直接返回该值int ret=1; // 初始化以pos位置为结尾的最长递增子序列的长度为1for(int i=pos+1;i<nums.size();i++) // 遍历nums数组,从pos+1开始{if(nums[i]>nums[pos]) // 如果当前元素大于pos位置的元素ret=max(ret,dfs(i,nums,memo)+1); // 更新以pos位置为结尾的最长递增子序列的长度}memo[pos]=ret; // 将计算出的以pos位置为结尾的最长递增子序列的长度存入memo数组return ret; // 返回以pos位置为结尾的最长递增子序列的长度}
};5. 解法3(动态规划):
5.1 算法思路:
-
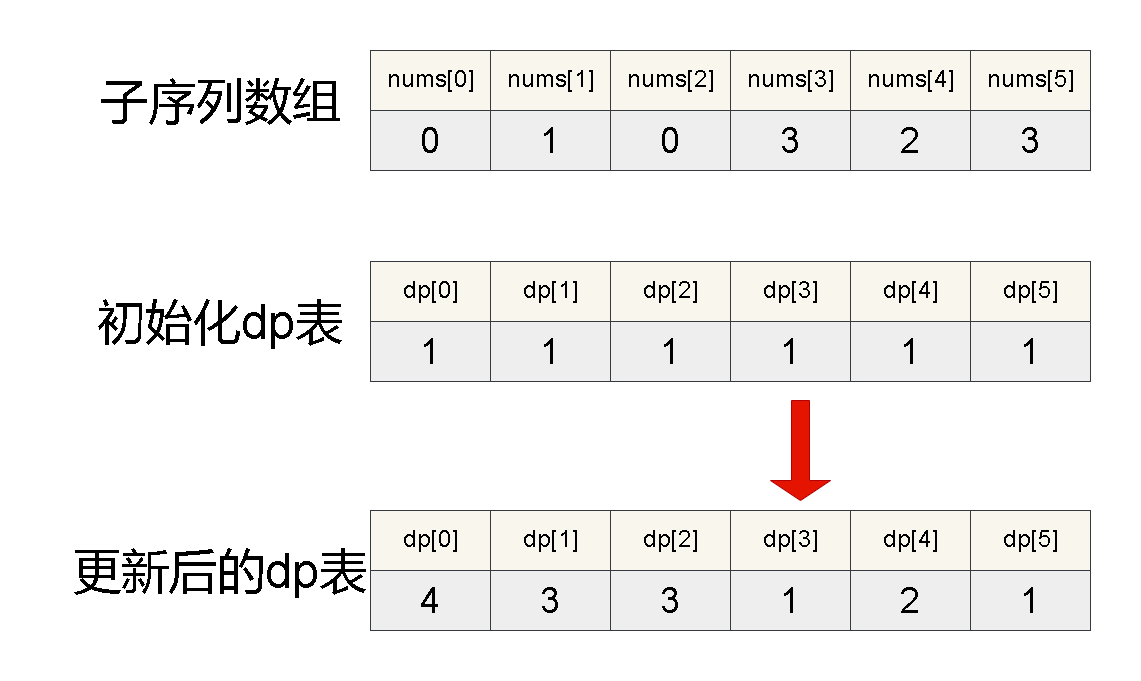
递归含义->状态表示
-
函数体->状态转移方程
-
递归出口->初始化
5.2 C++算法代码:
class Solution {
public:// 计算最长递增子序列的长度int lengthOfLIS(vector<int>& nums) {int n = nums.size(); // 获取数组长度vector<int> dp(n, 1); // 初始化动态规划数组,dp[i]表示以nums[i]结尾的最长递增子序列的长度int ret = 0; // 初始化最长递增子序列的长度为0// 从后往前遍历数组for (int i = n - 1; i >= 0; i--) {// 遍历当前元素之后的元素for (int j = i + 1; j < n; j++) {// 如果当前元素大于后面的元素,更新dp[i]的值if (nums[j] > nums[i]) {dp[i] = max(dp[i], dp[j] + 1);}}ret = max(ret, dp[i]); // 更新最长递增子序列的长度}return ret; // 返回最长递增子序列的长度}
};