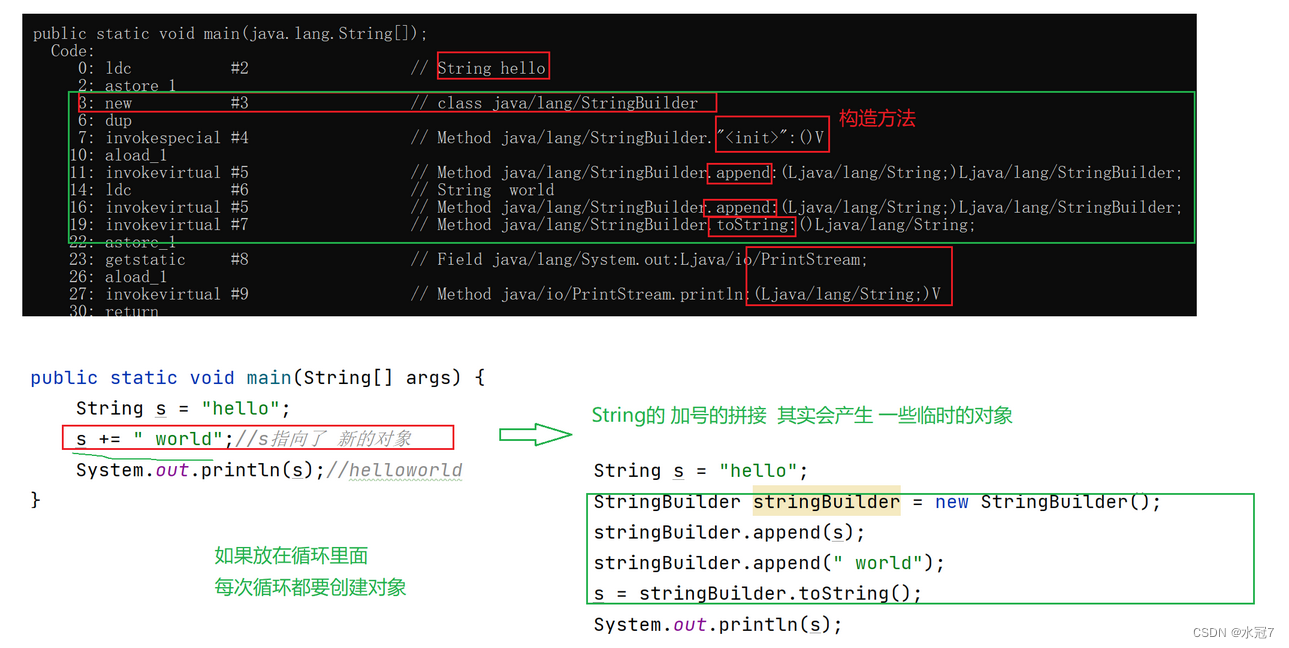
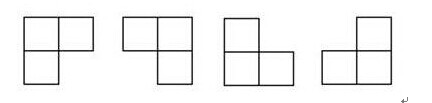
题目
在一个2^k * 2^k个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。在棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
输入
第一行为k,如题意
第二行为特殊点的坐标x,y
输出
特殊点用0输出,数据间用制表符隔开(‘t’), 要求遍历顺序按从左到右,从上到下。
样例输入
3 2 2
样例输出
3 3 4 4 8 8 9 9 3 0 2 4 8 7 7 9 5 2 2 6 10 10 7 11 5 5 6 6 1 10 11 11 13 13 14 1 1 18 19 19 13 12 14 14 18 18 17 19 15 12 12 16 20 17 17 21 15 15 16 16 20 20 21 21
分析
该题采用是分治的思想,就是把大问题分解成一个小问题进行解答,比如:8X8的棋盘可以从2X2的棋盘着手,分别有4种L型骨牌: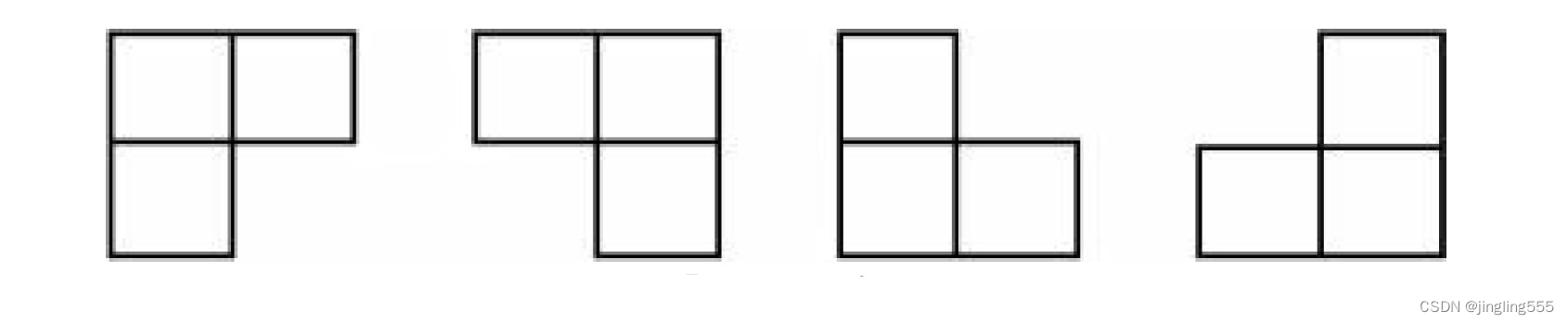
将 2^k*2^k的棋盘划分为 2^(k−1)∗2^(k−1)这样的子棋盘4块。
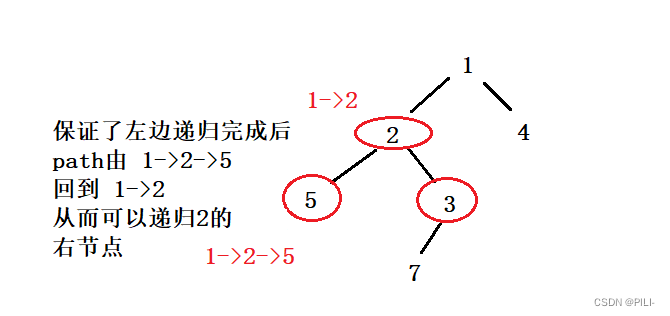
递归求解:递归填充各个格子,填充分为四个情况,
(1)如果特殊方块在左上子棋盘,则递归填充左上子棋盘;否则填充左上子棋盘的右下角,将右下角看做特殊方块,然后递归填充左上子棋盘。
(2)如果特殊方块在右上子棋盘,则递归填充右上子棋盘;否则填充右上子棋盘的左下角,将左下角看做特殊方块,然后递归填充右上子棋盘。
(3)如果特殊方块在左下子棋盘,则递归填充左下子棋盘;否则填充左下子棋盘的右上角,将右上角看做特殊方块,然后递归填充左下子棋盘。
(4)如果特殊方块在右下子棋盘,则递归填充右下子棋盘;否则填充右下子棋盘的右下角,将左上角看做特殊方块,然后递归填充右下子棋盘。
递归出口为 k=0也就是子棋盘方格数为1。
注意:这里的样例输入的特殊点坐标(2,2)是以1为起始坐标的,所以得在main函数里面调用ChessBoard(0,0,x-1,y-1,bs),所以就-1。
代码
//分治棋盘
#include <stdio.h>
#include <math.h>
int tile = 1;
int bd[128][128];
void ChessBoard(int tr, int tc, int dr, int dc, int sz) {if (sz == 1) return;int t = tile++;int s = sz / 2;//覆盖左上角子棋盘if (dr < tr + s && dc < tc + s) {ChessBoard(tr, tc, dr, dc, s);//特殊方格在此棋盘中}else {bd[tr + s - 1][tc + s - 1] = t;//用t号L型骨牌覆盖右下角ChessBoard(tr, tc, tr + s - 1, tc + s - 1, s);}//覆盖右上角子棋盘if (dr < tr + s && dc >= tc + s) {ChessBoard(tr, tc + s, dr, dc, s);}else {bd[tr + s - 1][tc + s] = t;//用t号L型骨牌覆盖左下角ChessBoard(tr, tc + s, tr + s - 1, tc + s, s);}//覆盖左下角子棋盘if (dr >= tr + s && dc < tc + s) {ChessBoard(tr + s, tc, dr, dc, s);}else {bd[tr + s][tc + s - 1] = t;//用t号L型骨牌覆盖右上角ChessBoard(tr + s, tc, tr + s, tc + s - 1, s);}//覆盖右下角子棋盘if (dr >= tr + s && dc >= tc + s) {ChessBoard(tr + s, tc + s, dr, dc, s);}else {bd[tr + s][tc + s] = t;//用t号L型骨牌覆盖左上角ChessBoard(tr + s, tc + s, tr + s, tc + s, s);}
}int main() {int n = 0, x = 0, y = 0,i,j;scanf("%d", &n);int bs = pow(2, n);//棋盘长度scanf("%d %d", &x, &y);ChessBoard(0, 0, x-1, y-1, bs);for (i = 0; i < bs; i++) {for (j = 0; j < bs; j++) {printf("%d\t", bd[i][j]);}printf("\n");}return 0;
}