AVL树

1. AVL树的概念

二叉搜索树可以缩短查找的效率，但是如果数据接近有序二叉搜索树将会退化为单支，查找元素相当于在顺序表中搜索元素，效率低下。

当向二叉搜索树当中插入新节点后，保证每个节点的左右子树高度之差的绝对值不超过1（需要对树中的节点进行调整）即可降低树的高度，从而减少平均搜索长度

一棵AVL树或者空树：

它的左右子树都是AVL树
左右子树高度只差（简称平衡因子）的绝对值不超过1

如果一棵二叉搜索树的高度是平衡的，它就是AVL树。

平衡因子：左边高是-1，右边高是1。左右高度相等则是0

2. AVL树节点的定义

template<class T>
struct AVLTreeNode {
public:explicit AVLTreeNode(const T& data): _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}AVLTreeNode<T>* _left;AVLTreeNode<T>* _right;AVLTreeNode<T>* _parent;T _data;int _bf;
};

3. AVL树的插入

AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树其实还是一棵二叉搜索树。AVL树的插入分为两步：

按照二叉搜索树的方式插入新节点
调整节点的平衡因子

cur 插入后，parent的平衡因子一定要调整，在插入之前parent的平衡因子分为三种情况：0， -1， 1。

分为以下两种情况：

如果cur插入到parent的左侧，parent的平衡因子-1
如果cur插入到parent的右侧，parent的平衡因子+1

这个时候parent的平衡因子分为三种情况：

如果parent的平衡因子是0，说明插入之前的平衡因子是正负1 插入成功
如果parent的平衡因子是正负1，说明插入之前是0，插入后更新为正负1，此时以parent为根的树的高度增加，需要继续向上更新
如果parent的平衡因子为正负2 ，则parent的平衡因子违反了平衡树的性质，需要对其进行旋转

4. AVL树的旋转

根据节点位置的不同，AVL树的旋转分为四种：

新节点插入较高左子树的左侧：右单旋

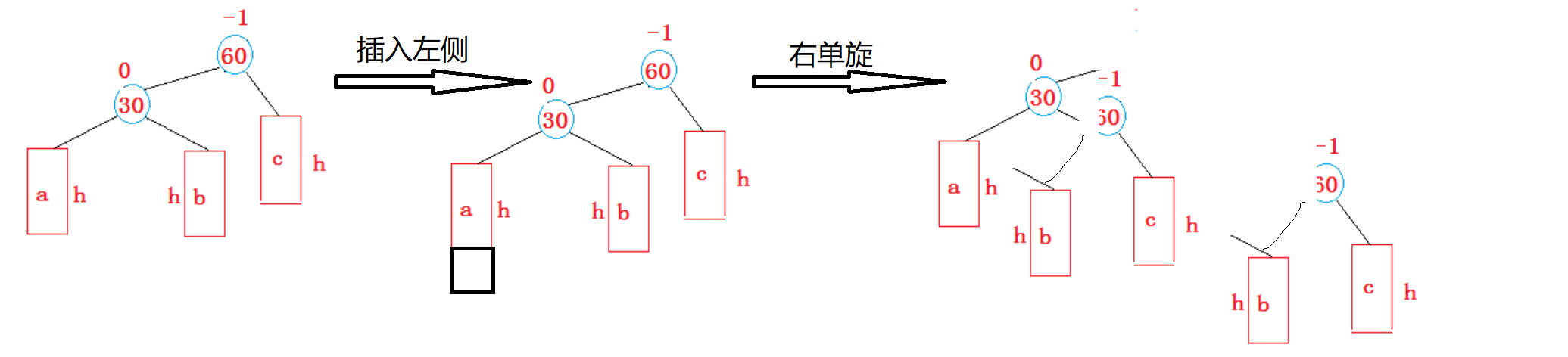
void rotateR(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;// 双亲的左为双亲左孩子的右孩子parent->_left = subLR;if (subLR) {subLR->_parent = parent;}subL->_right = parent;// 如果parent为子树Node* pParent = parent->_parent;parent->_parent = subL;subL->_parent = pParent;if (pParent == nullptr) {_root = subL;subL->_parent = nullptr;} else {// 如果parent是一个子树if (parent->_right == parent) {parent->_right = subL;} else {parent->_left = subL;}subL->_parent = pParent;}pParent->_bf = subL->_bf = 0;
}

新节点插入较高右子树的右侧：左单旋

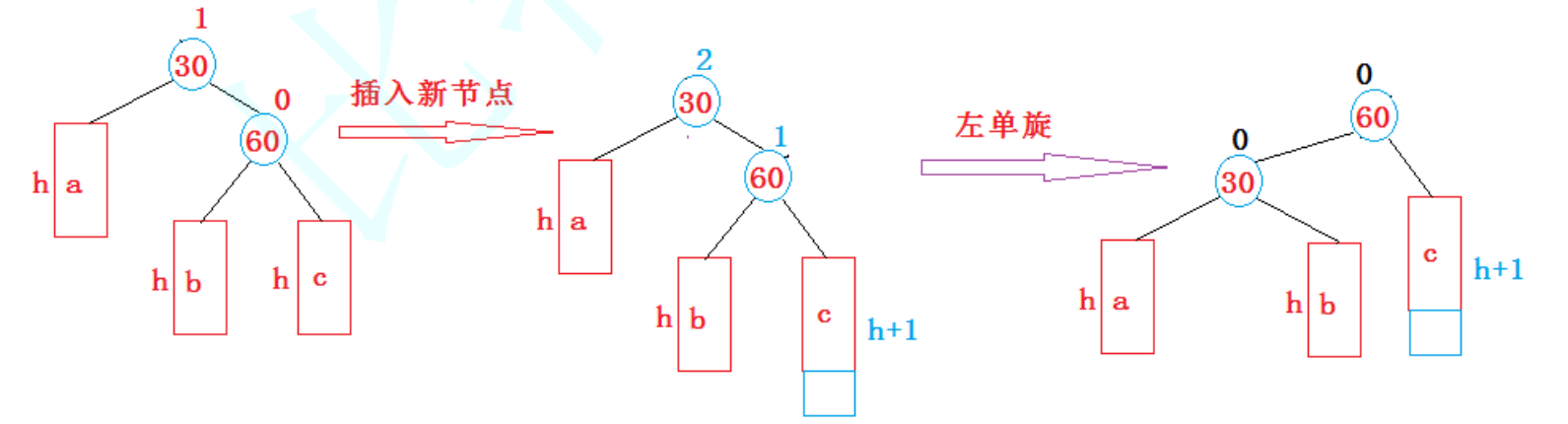
void rotateL(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL) {subRL->_parent = parent;}subR->_left = parent;Node* pParent = parent->_parent;parent->_parent = subR;if (pParent == nullptr) {_root = subR;subR->_parent = nullptr;} else {if (pParent->_left == subR) {pParent->_left = subR;} else {pParent->_right = subR;}subR->_parent = pParent;}
}

新节点插入较高左子树的右侧：先左单旋再右单旋

void rotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 1){parent->_bf = 0;subLR->_bf = 0;subL->_bf = -1;}else if (bf == -1){parent->_bf = 1;subLR->_bf = 0;subL->_bf = 0;}else if (bf == 0){parent->_bf = 0;subLR->_bf = 0;subL->_bf = 0;}else{assert(false);}
}

左单旋是指将一个节点的右子树提升为根节点，同时将原根节点降为左子树的右子节点。右单旋则是将一个节点的左子树提升为根节点，同时将原根节点降为右子树的左子节点。

判断应该使用左单旋还是右单旋，需要根据具体的情况来确定。一般来说，当某个节点的左子树高度大于右子树高度时，需要进行右单旋；当某个节点的右子树高度大于左子树高度时，需要进行左单旋。这是因为旋转操作可以通过改变树的结构来使得树重新平衡，使得左右子树的高度差保持在可接受的范围内。

新节点插入较高右子树的左侧：先右单旋再左单旋

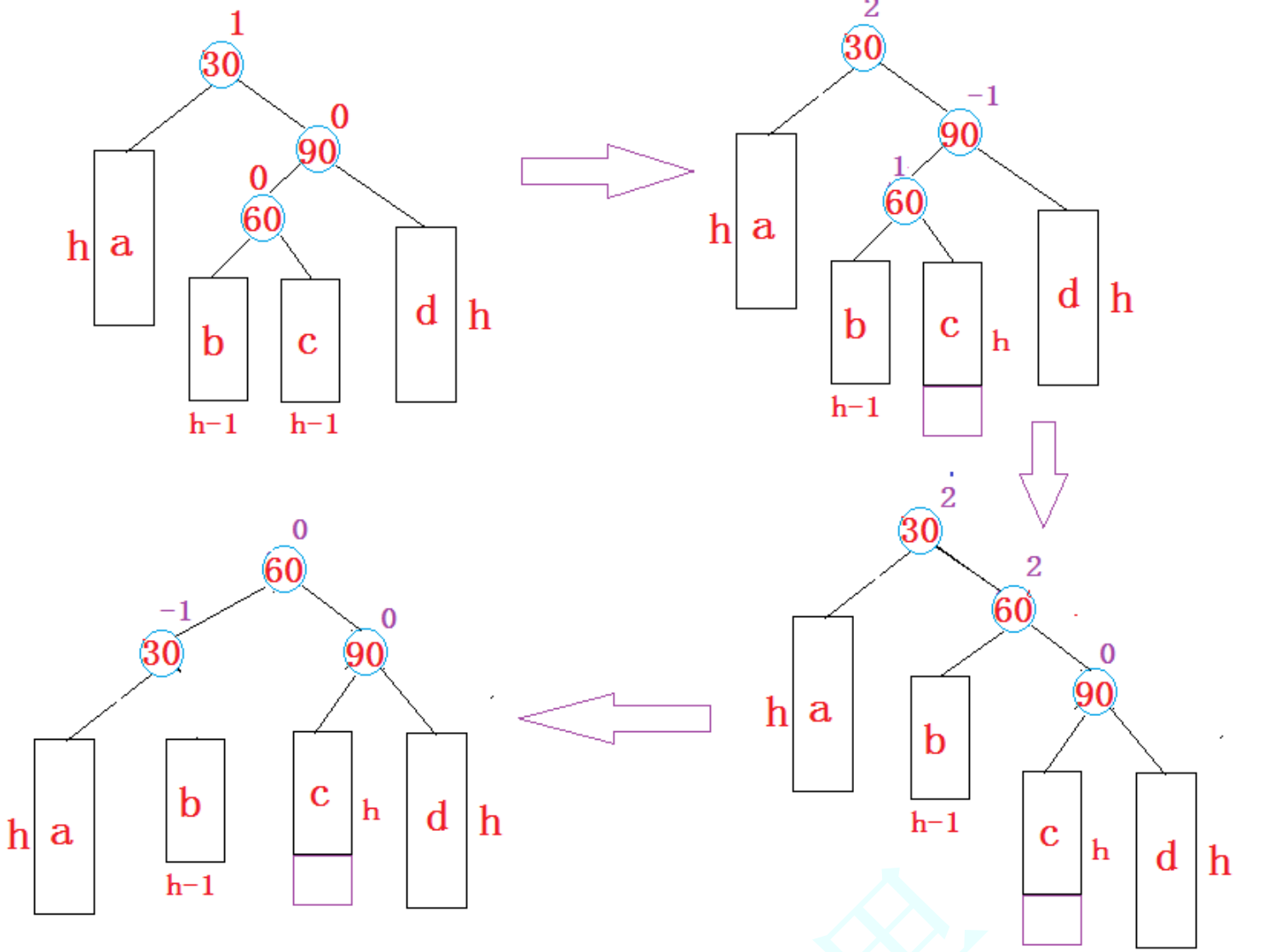
void rotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 1){subR->_bf = 0;parent->_bf = -1;subRL->_bf = 0;}else if (bf == -1){subR->_bf = 1;parent->_bf = 0;subRL->_bf = 0;}else if (bf == 0){subR->_bf = 0;parent->_bf = 0;subRL->_bf = 0;}else{assert(false);}
}