🚀个人主页:为梦而生~ 关注我一起学习吧!
💡专栏:机器学习 欢迎订阅!后面的内容会越来越有意思~
⭐特别提醒:针对机器学习,特别开始专栏:机器学习python实战 欢迎订阅!本专栏针对机器学习基础专栏的理论知识,利用python代码进行实际展示,真正做到从基础到实战!
💡往期推荐:
【机器学习基础】机器学习入门(1)
【机器学习基础】机器学习入门(2)
【机器学习基础】机器学习的基本术语
【机器学习基础】机器学习的模型评估(评估方法及性能度量原理及主要公式)
【机器学习基础】一元线性回归(适合初学者的保姆级文章)
【机器学习基础】多元线性回归(适合初学者的保姆级文章)
【机器学习基础】对数几率回归(logistic回归)
💡本期内容:针对前面的三个模型,在使用他们进行实际预测与分类时,会产生一系列对于不同的数据集的特别的问题,这篇文章就来有针对性的说一下!
文章目录
- 1 过拟合问题
- 1.1 回归问题中的过拟合
- 1.2 分类问题中的过拟合
- 1.3 如何解决
- 2 代价函数(cost function)
- 2.1 正则化参数
- 3 基于正则化的线性回归
- 3.1 加入正则化参数后的梯度下降算法
- 3.2 加入正则化参数后的正规方程
- 4 基于正则化的逻辑回归
1 过拟合问题
如果我们有非常多的特征,我们通过学习得到的假设可能能够非常好地适应训练集(代价函数可能几乎为 0),但是可能会不能推广到新的数据。
1.1 回归问题中的过拟合
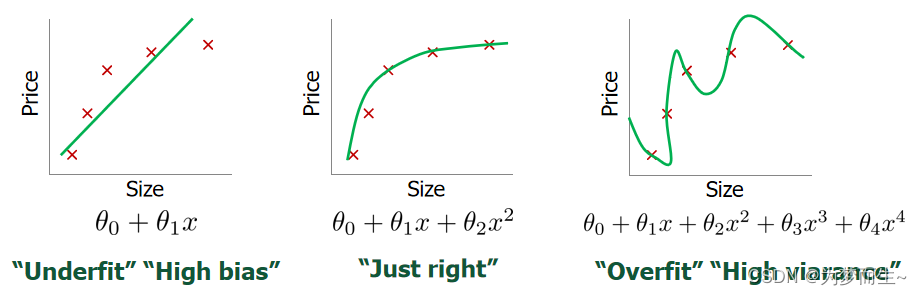
在线性回归中,我们可能遇到上面这几个问题:
第一个属于高偏差,欠拟合,不能很好地适应我们的训练集;
第三个属于高方差,模型过于强调拟合原始数据,而不能适应新的数据集,属于过拟合。
我们可以看出,若给出一个新的值使之预测,它将表现的很差,是过拟合,虽然能非常好地适应我们的 训练集但在新输入变量进行预测时可能会效果不好;而中间的模型似乎最合适。
1.2 分类问题中的过拟合
同样,在逻辑回归中,我们也可能遇到这些问题:
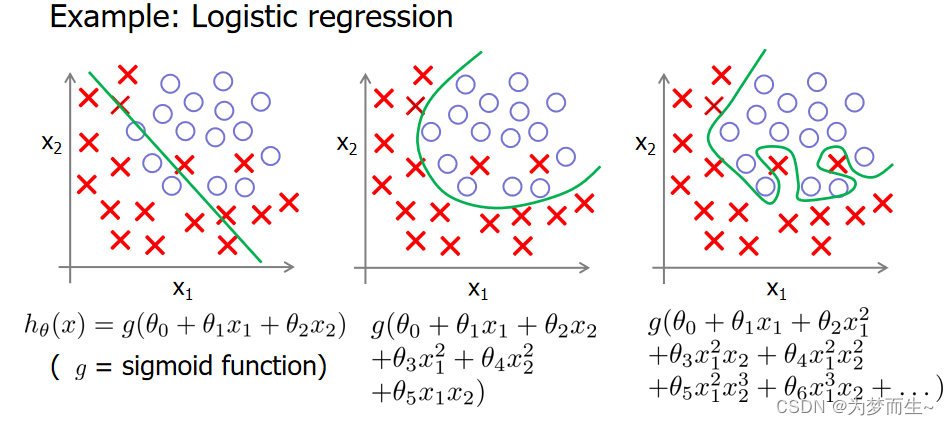
𝑥 的次数越高,拟合的越好,但相应的预测的能力就可能变差。
1.3 如何解决
问题是,如果我们发现了过拟合问题,应该如何处理?
- 丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,或者使用一 些模型选择的算法来帮忙(例如 PCA)
- 正则化。 保留所有的特征,但是减少参数的大小(magnitude)。
2 代价函数(cost function)
上面的回归问题中如果我们的假设函数是 h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 2 + θ 3 x 3 3 + θ 4 x 4 4 ℎ_{\theta} (x) = \theta_0 + \theta_1x_1 + \theta_2x_2^2 + \theta_3x_3^ 3 + \theta_4x_4^4 hθ(x)=θ0+θ1x1+θ2x22+θ3x33+θ4x44
我们可以从之前的事例中看出,正是那些高次项导致了过拟合的产生,所以如果我们能让这些高次项的系数接近于 0 的话,我们就能很好的拟合了。 所以我们要做的就是在一定程度上减小这些参数𝜃 的值,这就是正则化的基本原理。我 们决定要减少𝜃3和𝜃4的大小,我们要做的便是修改代价函数,在其中𝜃3和𝜃4 设置一点惩罚。 这样做的话,我们在尝试最小化代价时也需要将这个惩罚纳入考虑中,并最终导致选择较小 一些的𝜃3和𝜃4。
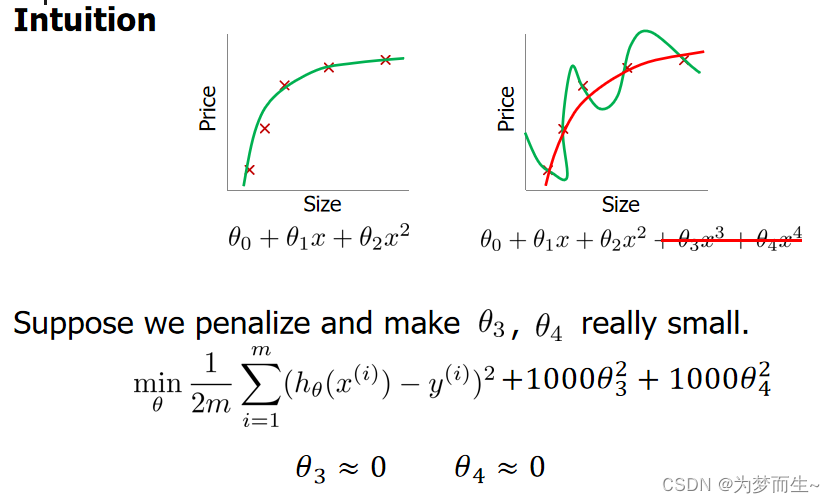
这样做的目的是弱化特征对拟合模型的影响,在不减少特征的情况下改变特征的权重。
2.1 正则化参数
然而我们并不知道其中哪些特征我们要惩罚,我们将对所有的特征进行惩罚, 并且让代价函数最优化的软件来选择这些惩罚的程度。
将这样的想法与前面线性回归模型中的代价函数结合后,得到了一个较为简单的能防止过拟合问题的代价函数:
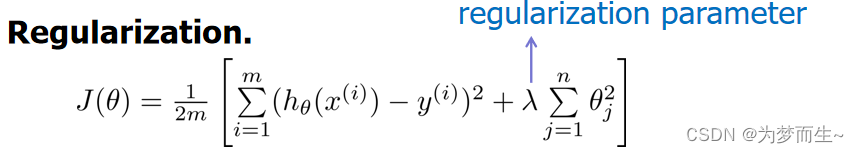
其中𝜆又称为正则化参数(Regularization Parameter)。
注:根据惯例,我们不对𝜃0 进 行惩罚。
如果选择的正则化参数 λ 过大,则会把所有的参数都最小化了,导致模型变成 ℎ𝜃 (𝑥) = 𝜃0,造成欠拟合。
- 为什么𝜆可以使𝜃的值减小呢
为如果我们令 𝜆 的值很大的话,为了使 Cost Function 尽可能的小,所有的 𝜃 的值 (不包括𝜃0)都会在一定程度上减小。
但若 λ 的值太大了,那么𝜃(不包括𝜃0)都会趋近于 0,这样我们所得到的只能是一条 平行于𝑥轴的直线。 所以对于正则化,我们要取一个合理的 𝜆 的值,这样才能更好的应用正则化。
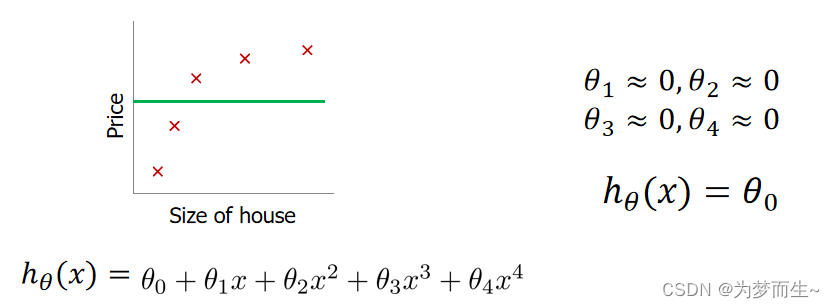
3 基于正则化的线性回归
对于线性回归的求解,我们之前推导了两种学习算法:一种基于梯度下降,一种基于正规方程。
【机器学习基础】一元线性回归(适合初学者的保姆级文章)
【机器学习基础】多元线性回归(适合初学者的保姆级文章)
3.1 加入正则化参数后的梯度下降算法
那么加入了正则化之后的线性回归代价函数变成了这样:
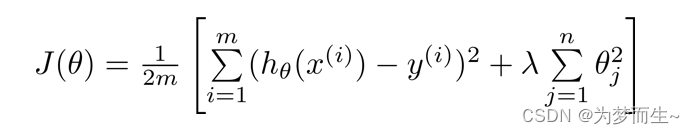
如果我们要使用梯度下降法求这个代价函数最小值,则梯度下降算法如下所示:

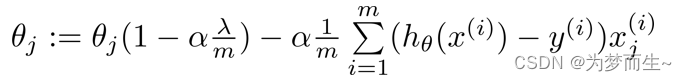
- 原理:
在𝜃j的系数变为(1-a𝜆/m),因为通常学习率a会较小,而m样本数量会较大,所以这个系数会很接近于1。可以看出正则化的梯度下降算法的变化在于,每次都在原有算法更新规则的基础上令𝜃减少一个额外的值(即每一次梯度下降都会对参数𝜃进行惩罚)。
3.2 加入正则化参数后的正规方程
假设输入和输出矩阵如下所示

θ \theta θ也是一个 n + 1 n+1 n+1维的矩阵,将他们代入代价函数后,展开并化简,就得到了带正则化项的正规方程:
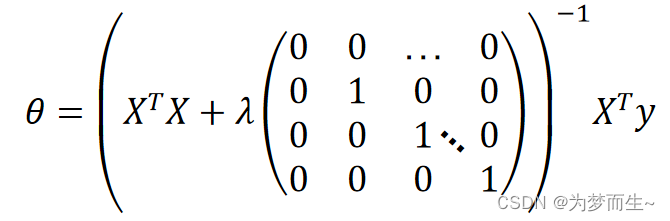
4 基于正则化的逻辑回归
针对逻辑回归问题,我们已经学习过两种优化算法:我们首先学习了使用梯度下降法来优化代价函数𝐽(𝜃),接下来学习了更高级的优化算法,这些高级优化算法需要你自己设计代价函数𝐽(𝜃)
自己计算导数同样对于逻辑回归,我们也给代价函数增加一个正则化的表达式,得到代价函数:

要最小化该代价函数,可以通过梯度下降算法: