线性变换

定义

设 $V$ 和 $W$ 都是在域$K$上定义的向量空间，$T:V\to W$ 对任二向量 $x,y\in V$,与任何标量 $a\in K$，满足：

• $T(x+y)=T(x)+T(y)$
• $T(ax)=aT(x)$

则$T$ 被称为是线性变换。

线性算子：从向量空间U映射到U的线性变换

$0$变换： $0(x)=0$

自身算子：$I(x)=x$

对于$A\in {\mathcal{R}}^{m\times n},x\in {\mathcal{R}}^{m\times 1}$，函数$T(x)=Ax$是一个从${\mathcal{R}}^n$到${\mathcal{R}}^m$线性变换，如果$A$是$n\times n$的话，$T$是一个线性算子。

若 B = { u 1 , u 2 , … , u n } \mathcal B =\{ u_1,u_2,\dots,u_n\} B={u1​,u2​,…,un​}是向量空间U的一组基，且$v={\alpha }_1{u}_1+{\alpha }_2{u}_2+\cdots +{\alpha }_n{u}_n$，则表示为$[v{]}_{\mathcal{B}}=({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n{)}^T$。

若 A = { e 1 , e 2 , … , e n } \mathcal A =\{ e_1,e_2,\dots,e_n\} A={e1​,e2​,…,en​}，则被称为向量空间的标准基

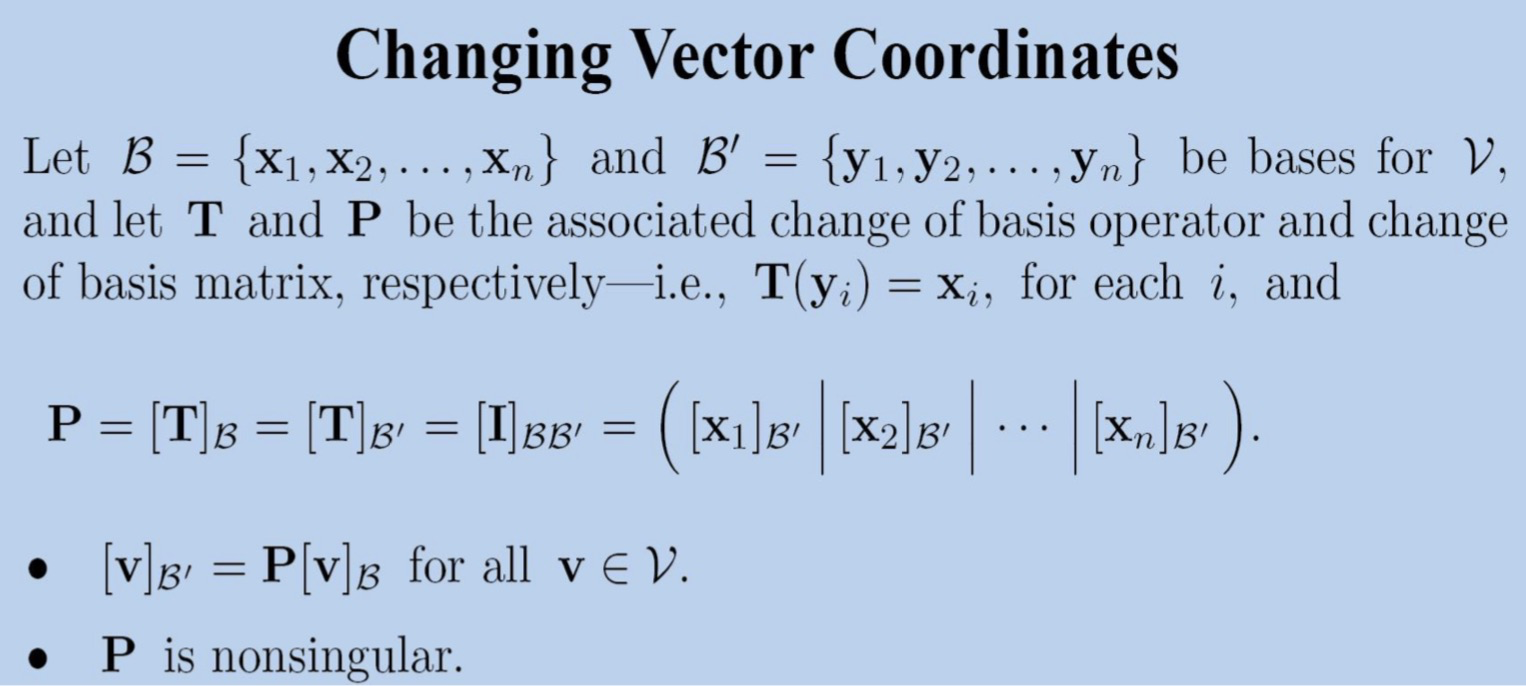
若 B = { x 1 , x 2 , … , x n } \mathcal B=\{x_1,x_2,\dots,x_n\} B={x1​,x2​,…,xn​}与 B ′ = { y 1 , y 2 , … , y n } \mathcal B'=\{y_1,y_2,\dots,y_n\} B′={y1​,y2​,…,yn​}分别为向量空间$V$的两组基，其中存在一个变换$A$在基$\mathcal{B}$的表示，则$[A{]}_{{\mathcal{B}}^{\prime }}=[A[x_1{]}_{{\mathcal{B}}^{\prime }},A[x_2{]}_{{\mathcal{B}}^{\prime }},\dots ,A[x_n{]}_{{\mathcal{B}}^{\prime }}]$表示

其中$[I{]}_{{\mathcal{B}}^{\prime }\mathcal{B}}$为在向量空间上基向量${\mathcal{B}}^{\prime }$用$\mathcal{B}$表示

例题1

设 $T$ 为 $R^3$ 的一个线性算子，其定义为 $T(x,y,z)=(x-y,y-x,x-z)$ ,$\mathcal{B}=\left\{u_1=\left(\begin{array}{c}1\\ 0\\ 1\end{array}\right),u_2=\left(\begin{array}{c}0\\ 1\\ 1\end{array}\right),u_3=\left(\begin{array}{c}1\\ 1\\ 0\end{array}\right)\right\}$为其一组基，$v=\left(\begin{array}{c}1\\ 1\\ 0\end{array}\right)$为$R^3$的一个向量。

1)分别计算$[T{]}_{\mathcal{B}}$和$[v{]}_{\mathcal{B}}$

2)计算$[T(v){]}_{\mathcal{B}}$，并验证$[T(v){]}_{\mathcal{B}}=[T{]}_{\mathcal{B}}[v{]}_{\mathcal{B}}$ 成立。

1）

首先我们计算$[T{]}_{\mathcal{B}}$，它是由$T$作用在基向量上得到的各结果的坐标向量

$[T(u_i){]}_{\mathcal{B}}$ （$i=1,2,3$）组成。即 $$\begin{array}{rl}[T(u_1){]}_{\mathcal{B}}& =[T(1,0,1){]}_{\mathcal{B}}=[(1,-1,0){]}_{\mathcal{B}},\\ [T(u_2){]}_{\mathcal{B}}& =[T(0,1,1){]}_{\mathcal{B}}=[(-1,1,-1){]}_{\mathcal{B}},\\ [T(u_3){]}_{\mathcal{B}}& =[T(1,1,0){]}_{\mathcal{B}}=[(0,0,1){]}_{\mathcal{B}}.\end{array}$$

将以上各向量转化为$\mathcal{B}$下的坐标向量需要解以下方程：

For $[T(u_1){]}_{\mathcal{B}}$: $$\left(\begin{array}{c}1\\ -1\\ 0\end{array}\right)=a\left(\begin{array}{c}1\\ 0\\ 1\end{array}\right)+b\left(\begin{array}{c}0\\ 1\\ 1\end{array}\right)+c\left(\begin{array}{c}1\\ 1\\ 0\end{array}\right).$$

解得：$a=1,b=-1,c=0$

For $[T(u_2){]}_{\mathcal{B}}$: $$\left(\begin{array}{c}-1\\ 1\\ -1\end{array}\right)=a\left(\begin{array}{c}1\\ 0\\ 1\end{array}\right)+b\left(\begin{array}{c}0\\ 1\\ 1\end{array}\right)+c\left(\begin{array}{c}1\\ 1\\ 0\end{array}\right).$$

解得：$a=-\frac{3}{2},b=\frac{1}{2},c=\frac{1}{2}$

For $[T(u_3){]}_{\mathcal{B}}$: $$\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)=a\left(\begin{array}{c}1\\ 0\\ 1\end{array}\right)+b\left(\begin{array}{c}0\\ 1\\ 1\end{array}\right)+c\left(\begin{array}{c}1\\ 1\\ 0\end{array}\right).$$

解得：$a=\frac{1}{2},b=\frac{1}{2},c=-\frac{1}{2}$

解以上各方程，我们可以得到对应的坐标向量。

此外，我们还需要求$R^3$中的向量$v$在基$\mathcal{B}$上的坐标向量$[v{]}_{\mathcal{B}}$, 它可通过解以下方程得出 $$\left(\begin{array}{c}1\\ 1\\ 0\end{array}\right)=a\left(\begin{array}{c}1\\ 0\\ 1\end{array}\right)+b\left(\begin{array}{c}0\\ 1\\ 1\end{array}\right)+c\left(\begin{array}{c}1\\ 1\\ 0\end{array}\right)=a{u}_1+b{u}_2+c{u}_3$$

解得：$a=1,b=1,c=0$

综上所述：

$[T{]}_{\mathcal{B}}=\left[\begin{array}{ccc}1& -\frac{3}{2}& \frac{1}{2}\\ -1& \frac{1}{2}& \frac{1}{2}\\ 0& \frac{1}{2}& -\frac{1}{2}\end{array}\right]$

$[v{]}_{\mathcal{B}}=\left[\begin{array}{c}1\\ 1\\ 0\end{array}\right]$

2）

$T(v)=\left(\begin{array}{c}0\\ 0\\ -1\end{array}\right)$

$[T(v){]}_{\mathcal{B}}=a\left(\begin{array}{c}1\\ 0\\ 1\end{array}\right)+b\left(\begin{array}{c}0\\ 1\\ 1\end{array}\right)+c\left(\begin{array}{c}1\\ 1\\ 0\end{array}\right)$

解得$[T(v){]}_b=\left(\begin{array}{c}-\frac{1}{2}\\ -\frac{1}{2}\\ \frac{1}{2}\end{array}\right)$

所以$[T(v){]}_{\mathcal{B}}=[T{]}_{\mathcal{B}}[v{]}_{\mathcal{B}}$

例题2

设 $$A(x,y,z)=(x+2y-z,-y,x+7z)$$为 $$R^3$$ 的一个线性算子，其定义为 $$T(x,y,z)=(x-y,y-x,x-z)$$ ,$$\mathcal{B}=\left\{\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right),\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right),\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)\right\},{\mathcal{B}}^{\prime }=\left\{\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right),\left(\begin{array}{c}1\\ 1\\ 0\end{array}\right),\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)\right\}$$为其一组基，$$v=\left(\begin{array}{c}1\\ 1\\ 0\end{array}\right)$$为$$R^3$$的一个向量。

1)分别计算$$[A{]}_{\mathcal{B}}$$和$$[A{]}_{{\mathcal{B}}^{\prime }}$$

2)求矩阵$$Q$$，使得$$[A{]}_{{\mathcal{B}}^{\prime }}=Q^{-1}[A{]}_{\mathcal{B}}Q$$成立。

首先，我们需要找出在$$\mathcal{B}$$和$${\mathcal{B}}^{\prime }$$基下的矩阵$$A$$的表示即$$[A{]}_{\mathcal{B}}$$和$$[A{]}_{{\mathcal{B}}^{\prime }}$$。这一步可以通过将线性变换应用于基向量并将结果写成列向量的形式完成。

线性算子$$A$$以$$\mathcal{B}$$为基的矩阵表示为： $$[A{]}_{\mathcal{B}}={\left[\begin{array}{ccc}A(1,0,0)& A(0,1,0)& A(0,0,1)\end{array}\right]}_{\mathcal{B}}$$ $$=[A(e_1),A(e_2),A(e_3){]}_{\mathcal{B}}$$

计算得到 $$[A{]}_{\mathcal{B}}={\left[\begin{array}{ccc}A(1,0,0)& A(0,1,0)& A(0,0,1)\end{array}\right]}_{\mathcal{B}}=\left[\begin{array}{ccc}1& 2& -1\\ 0& -1& 0\\ 1& 0& 7\end{array}\right]$$

线性算子$$A$$以$${\mathcal{B}}^{\prime }$$为基的矩阵表示为： $$[A{]}_{{\mathcal{B}}^{\prime }}={\left[\begin{array}{ccc}A(1,0,0)& A(1,1,0)& A(1,1,1)\end{array}\right]}_{{\mathcal{B}}^{\prime }}$$ $$=[A(e_1^{\prime }),A(e_2^{\prime }),A(e_3^{\prime }){]}_{{\mathcal{B}}^{\prime }}$$

计算得到 $$[A{]}_{{\mathcal{B}}^{\prime }}={\left[\begin{array}{ccc}A(1,0,0)& A(1,1,0)& A(1,1,1)\end{array}\right]}_{{\mathcal{B}}^{\prime }}=\left[\begin{array}{ccc}1& 4& 3\\ -1& -2& 9\\ 1& 1& 8\end{array}\right]$$

接下来求矩阵$$Q$$，使得$$[A{]}_{{\mathcal{B}}^{\prime }}=Q^{-1}[A{]}_{\mathcal{B}}Q$$成立。

我们已经知道 B = { e 1 , e 2 , e 3 } \mathcal{B}=\{e_1,e_2,e_3\} B={e1​,e2​,e3​}和 B ′ = { e 1 ′ , e 2 ′ , e 3 ′ } \mathcal{B'}=\{e_1',e_2',e_3'\} B′={e1′​,e2′​,e3′​}。

给出两个基$\mathcal{B}$和${\mathcal{B}}^{\prime }$，要找出矩阵$I$在基${\mathcal{B}}^{\prime }$和$\mathcal{B}$之间的表示$[I{]}_{{\mathcal{B}}^{\prime }\mathcal{B}}$。 第一个基$\mathcal{B}$是标准基，我们考虑将${\mathcal{B}}^{\prime }$的基向量表示为$\mathcal{B}$的线性组合。具体地：

第一个基向量在${\mathcal{B}}^{\prime }$中是$\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)$，这就是$\mathcal{B}$的第一个基向量，所以在$\mathcal{B}$的基的表示下，首列是$(1,0,0{)}^T$。

第二个基向量在${\mathcal{B}}^{\prime }$中是$\left(\begin{array}{c}1\\ 1\\ 0\end{array}\right)$，它可以被表示为$\mathcal{B}$的第一个和第二个基向量的和，于是在$\mathcal{B}$的基的表示下，第二列是$(1,1,0{)}^T$。

第三个基向量在${\mathcal{B}}^{\prime }$中是$\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)$，它可以被表示为$\mathcal{B}$所有三个基向量的和，所以在$\mathcal{B}$的基的表示下，第三列是$(1,1,1{)}^T$。

以$\mathcal{B}$的基表示，我们得到： $$[I{]}_{{\mathcal{B}}^{\prime }\mathcal{B}}=\left(\begin{array}{ccc}1& 1& 1\\ 0& 1& 1\\ 0& 0& 1\end{array}\right)$$ 这就是矩阵$I$在${\mathcal{B}}^{\prime }$和$\mathcal{B}$之间的线性变换矩阵。

例题三

对于 $R^{2\times 2}$ 矩阵,$\mathcal B = \left{ \begin{bmatrix} 1 & 0 \ 0 & 0 \end{bmatrix}, \begin{bmatrix} 0 & 1 \ 0 & 0 \end{bmatrix}, \begin{bmatrix} 0 & 0 \ 1 & 0 \end{bmatrix}, \begin{bmatrix} 0 & 0 \ 0 & 1 \end{bmatrix} \right} $

对其中一组矩阵, 对于该运算中任意矩阵 $A$, 定义映射 T 定义如下：

$T(A) = \frac{A + A^T}{2} $

计算 $[T{]}_{\mathcal{B}}$.

首先我们需要了解一下所给出的映射$T$如何作用于一个矩阵。给定矩阵$A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$, 我们可以计算：

$$T(A)=\frac{A+A^T}{2}=\frac{\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]+\left[\begin{array}{cc}a& c\\ b& d\end{array}\right]}{2}=\left[\begin{array}{cc}a& \frac{b+c}{2}\\ \frac{b+c}{2}& d\end{array}\right]$$

为了找到矩阵$[T{]}_B$，我们需要将基$B$中的每一个矩阵分别带入$T$中，并表示其结果为$B$基下的坐标。

对于$\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]$:

$$T\left(\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]\right)=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]=1\cdot \left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]+0\cdot \left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]+0\cdot \left[\begin{array}{cc}0& 0\\ 1& 0\end{array}\right]+0\cdot \left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]$$

所以，第一列为$\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right]$。

对于$\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]$:

$$T\left(\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]\right)=\left[\begin{array}{cc}0& 0.5\\ 0.5& 0\end{array}\right]=0\cdot \left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]+0.5\cdot \left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]+0.5\cdot \left[\begin{array}{cc}0& 0\\ 1& 0\end{array}\right]+0\cdot \left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]$$

所以，第二列为$\left[\begin{array}{c}0\\ 0.5\\ 0.5\\ 0\end{array}\right]$。

对于$\left[\begin{array}{cc}0& 0\\ 1& 0\end{array}\right]$:

这个矩阵和上一个矩阵相同，所以第三列也是$\left[\begin{array}{c}0\\ 0.5\\ 0.5\\ 0\end{array}\right]$。

对于$\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]$:

$$T\left(\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]\right)=\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]=0\cdot \left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]+0\cdot \left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]+0\cdot \left[\begin{array}{cc}0& 0\\ 1& 0\end{array}\right]+1\cdot \left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]$$

所以，第四列为$\left[\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right]$。

综上，$[T{]}_{\mathcal{B}}$为:

$$[T{]}_{\mathcal{B}}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0.5& 0.5& 0\\ 0& 0.5& 0.5& 0\\ 0& 0& 0& 1\end{array}\right]$$