树拓扑序计数
叶向树拓扑序计数
朴素的做法是 dp 然后归纳,但是论文给出了新解释。
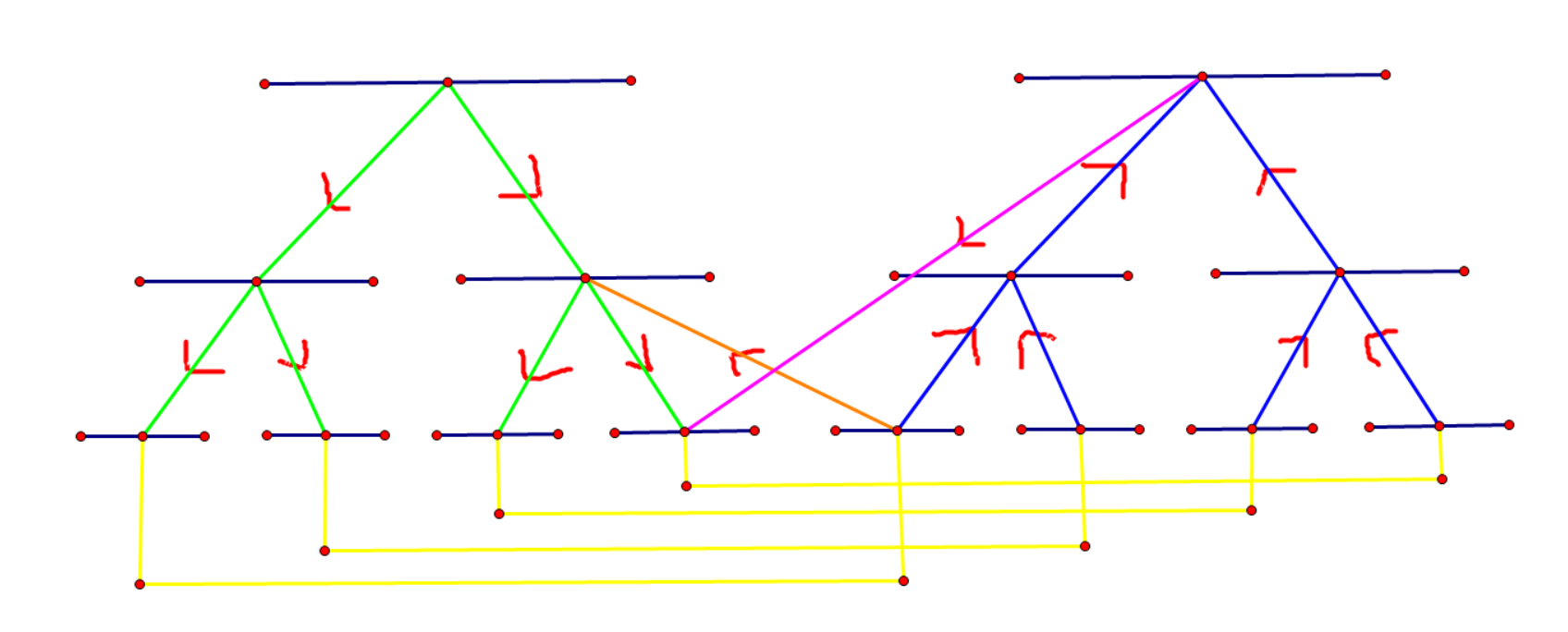
考察一个简单的拓扑序生成方式:你有一个集合,初始为空,每次选择树中不在集合里的一个点,取它最浅的不在集合里的点,加入集合,重复操作 \(n\) 次直到所有点均被加入,加入的顺序显然是一个拓扑序。
显然这样选点的方式有 \(n!\) 种,但是每个拓扑序会被算重,具体来说,第 \(i\) 次有 \(\text{size}(p_i)\) 种选法,于是每个拓扑序都会被算 \(\prod\limits_{u=1}^n\text{size}(u)\) 次,因此拓扑序方案数为 \(\frac{n!}{\prod\limits_{u=1}^n\text{size}(u)}\) 种。
 才发现原来我不会拓扑序计数。临时补一下。
才发现原来我不会拓扑序计数。临时补一下。




![[Tools] GitHub Action 部署文档网站](https://resource.duyiedu.com/xiejie/2023-06-09-063500.png)
![[Tools] VitePress搭建文档网站](https://resource.duyiedu.com/xiejie/2023-06-09-024255.jpg)