滑动窗口是什么?
滑动窗口其实是一个想象出来的数据结构。有左边界L和有边界R。
举例来说:数组 arr = {3,1,5,7,6,5,8}; 其窗口就是我们规定的一个运动轨迹。
最开始时,边界LR都在数组的最左侧,此时没有包住任何数。
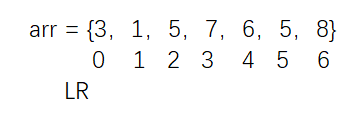
此时规定:
1.可以在任何时候让R只能往右滑动。此时一个数会从右侧进入窗口。直到滑动到终止位置8。因为再往右就没位置了。
2. 可以在任何时候让L只能往右滑动(但是不能超过R,到R右侧),此时一个数会从左侧出窗口。
在这种原则下,可以动态从窗口右侧进数,从窗口左侧出数。
R向右滑动经过了3,1,5,此时3个数依次从窗口右侧进入窗口。

此时R不动了,L向右滑动,那此时3这个数就从左侧出窗口。

规定好窗口后。因为LR可以在任何时候进行移动,所以此时窗口是个动态的。
那每次移动形成的窗口,客观上来讲都会有一个窗口内的最大值。那用什么办法可以来获取到窗口内最大值呢?
- 每次形成窗口,都进行遍历窗口内的值来取得最大值(复杂度太高)。
- 每次在形成窗口后,值在进出窗口时,可以迅速更新某种结构,以此来获取窗口内最大值。
双端队列
用双端队列(可以从头部进头部出、尾部进尾部出,时间复杂度( O ( 1 ) O(1) O(1)))来维护在任何状态下窗口内最大值的更新结构。
用双端队列维护最大值更新来举例:
一开始,假设窗口停留在数组左边,一个数没囊括,双端队列中没有任何东西。
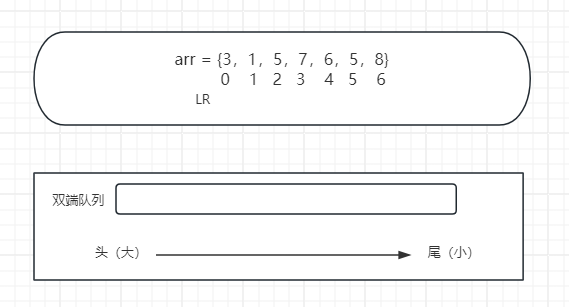
此时,R向右移动一个位置,来看双端队列中是如何变化的。
R向右移动,包裹了索引0位置上的3这个数,从尾端加到双端队列中去,在它加入之前,双端队列是空的,直接加入。窗口头部代表窗口内最大值,此时最大值为3。
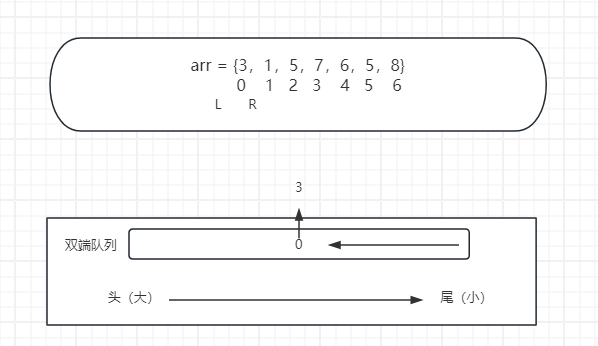
R再次向右滑动,囊括进索引1位置的1,因为没有破坏我规定的由大到小的原则,所以将1从尾端加入到队列中,此时队列有2个数,3和1,当前窗口内最大值为3。
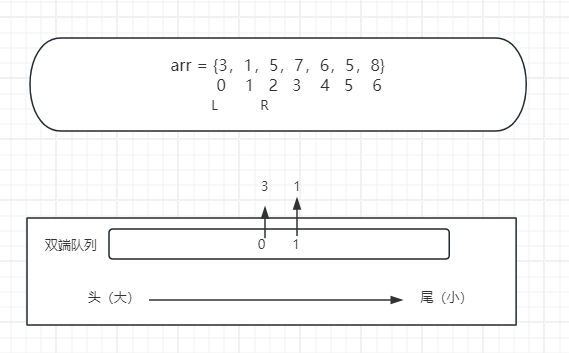
R再次移动,来到了2位置的5,此时队列中有0位置3和1位置的1,因为要求队列中的数要从大到小的顺序。所以不能直接将5加进来,那么弹出。因为3和1都比5小,所以将3和1从尾端弹出(弹出后不再找回,值相等也弹出)。将5加入。
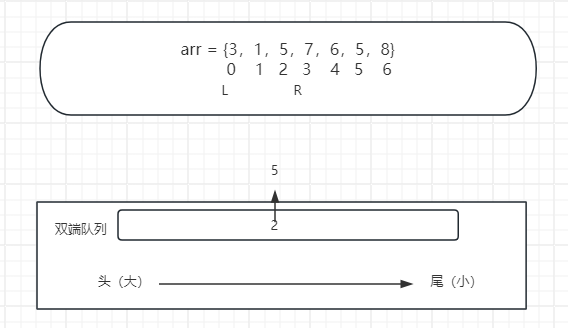
以此类推,这就是R向右移动时队列的更新情况。
双端队列的含义:
如果此时让窗口依次缩小,哪些位置的数会依次成为窗口内最大值。
上面描述了R向右移动时队列的情况。此时如果R来到了1位置后不动了,变成L向右移动,L++。
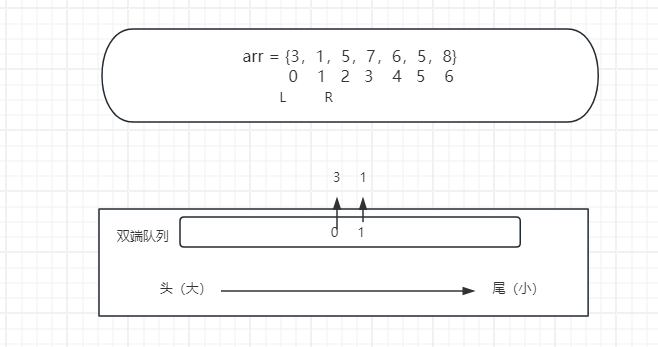
因为我L和R只能向右移动,不能回退,所以此时0位置的3会过期出队列,1位置1成为窗口内最大值。
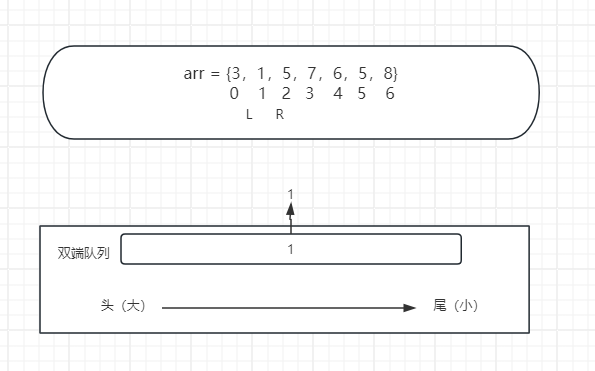
为什么R右移时要将比它本小的或者相等的数踢出队列呢?
因为不能回退,R从0下标向N下标处走,后进入队列的都是下标大的数,而R不动,想要缩小窗口的话,只能L++,L向右移动后,也是从0 ~ N 的运动轨迹,所以先进队列的先过期。所以不担心踢出队列后数组最大值的问题。
而L++弹出时,只需要判断队列当中头部的值是否等于当前值即可,等于即弹出,后面新的头部值就是双端队列中新的最大值。
总结:
窗口滑动过程中,假设LR会划过数组中所有数字,双端队列中每个数最多只会进来1次出去1次,并且踢出后不再找回。窗口运动过程中,双端队列更新总代价 O ( N ) O(N) O(N),均摊每个数时间复杂度就是 O ( 1 ) O(1) O(1)。