问题描述

最大子段和问题；

洛谷P1115.最大子段和

分治法

利用归并排序的方法，但是由于是算最大子段和所以，并不能将它变成有序的，左边和右边的最大子段和通过调用函数，而中间的要算左边最大，右边最大加起来才是中间的最大子段和
最后返回左，右， 中的最大值

#include <iostream>
#include <cstring>
#include <algorithm>
#define int long long 
using namespace std;const int N = 100010;int a[N], n;int max_subarray_sum(int l, int r) {if (l >= r) return a[l];int mid = l + r >> 1;int left_max = max_subarray_sum(l, mid);int right_max = max_subarray_sum(mid + 1, r);int left_border_max = 0, right_border_max = 0;int sum = 0;for (int i = mid; i >= l; i--) {sum += a[i];left_border_max = max(left_border_max, sum);}sum = 0;for (int i = mid + 1; i <= r; i++) {sum += a[i];right_border_max = max(right_border_max, sum);}int combined_max = left_border_max + right_border_max;return max({left_max, right_max, combined_max});
}signed main() {scanf("%lld", &n);for (int i = 0; i < n; i++) scanf("%lld", &a[i]);printf("%lld\n", max_subarray_sum(0, n - 1));return 0;
}

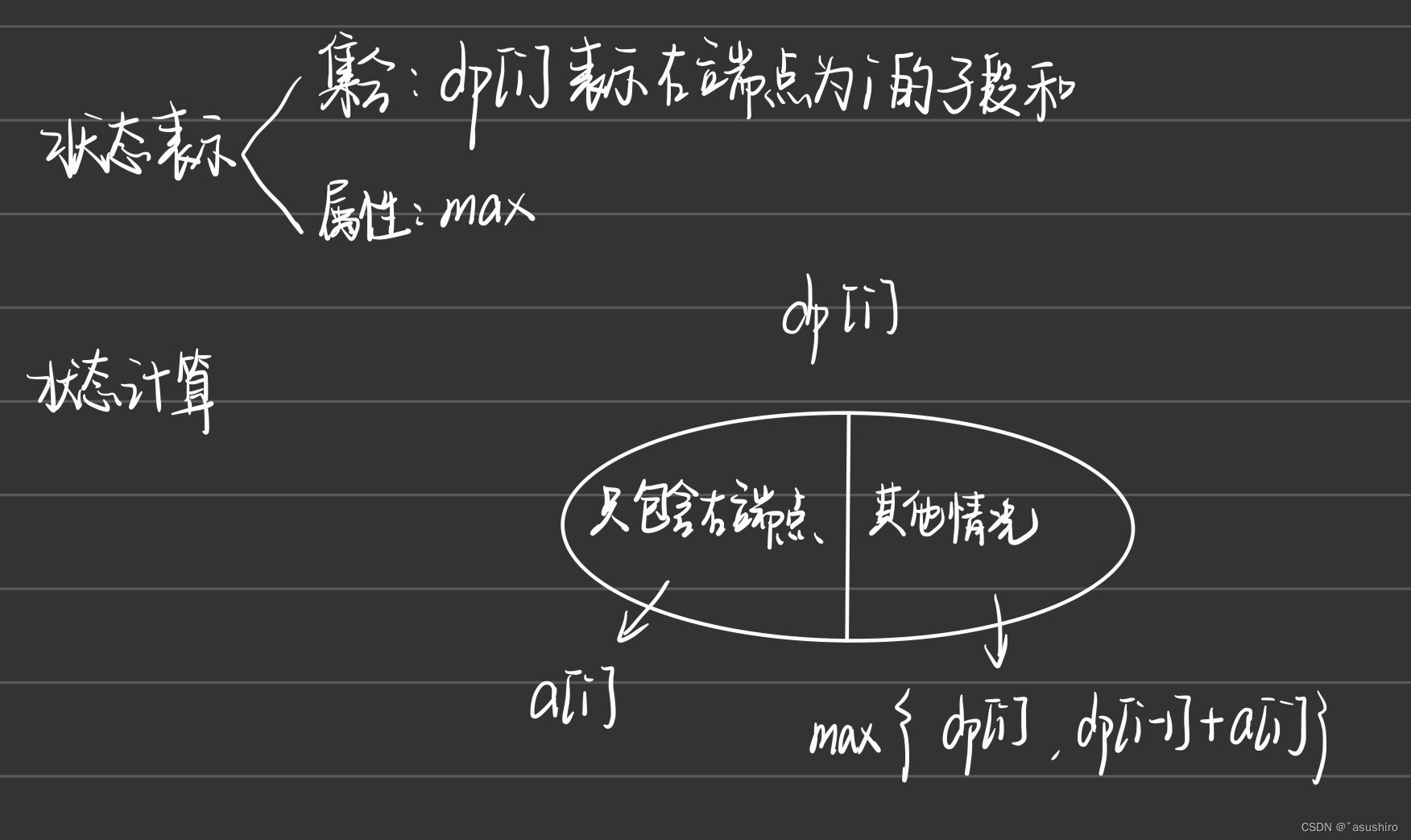
动态规划法

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 200010;int dp[N], a[N], n;int main()
{scanf("%d", &n);for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);int res = -1e8;for (int i = 1; i <= n; i ++){dp[i] = max(a[i], dp[i - 1] + a[i]);res = max(dp[i], res);}printf("%d", res);return 0;
}

由于状态计算只用到了数组的上一个元素，所以可以用一个变量表示滚动数组，这样就不用开一个数组了

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 200010;int a[N], n, dp;int main()
{scanf("%d", &n);for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);int res = -1e8;dp = 0;for (int i = 1; i <= n; i ++){dp = max(a[i], dp + a[i]);res = max(res, dp);}printf("%d", res);return 0;
}