1898D - Absolute Beauty
题意:给定长度为n的数组a和b,定义b数组的价值为,现可以交换一次b数组中的任意两个元素,求b数组的价值最大值。
思路:绝对值问题可以放在数轴上去解决。绝对值即为区间长度



观察上述三种情况,发现当且仅当第二种情况,即原本两段区间不重合的条件下,其b数组的价值才会增加,增加的值为他们两段区间相隔的距离乘2。手画一下后发现交换a、b不会对结果造成任何影响,因此本题转换为给定若干区间,求区间间隔最大。只需要记录一下一个区间的最小右端点和区间的最大左端点,然后他们之间的差就是最大区间间隔。
// Problem: D. Absolute Beauty
// Contest: Codeforces - Codeforces Round 910 (Div. 2)
// URL: https://codeforces.com/contest/1898/problem/D
// Memory Limit: 256 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
const LL maxn = 4e05+7;
const LL N=2e05+10;
const LL mod=1e09+7;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >t;
priority_queue<LL> q;
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
int a[N] , b[N];
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve()
{cin >> n;pair<int,int>p[n + 1];for(int i = 1 ; i <= n ; i ++){cin >> a[i];}for(int i = 1 ; i <= n ; i ++){cin >> b[i];}LL ans = 0;int r_min = 1e9 , l_max = 0;for(int i = 1 ; i <= n ; i ++){if(a[i] > b[i])swap(a[i] , b[i]);r_min = min(r_min , b[i]);l_max = max(l_max , a[i]);ans += abs(b[i] - a[i]);}if(r_min < l_max){ans += 2 * (l_max - r_min);}cout << ans<<endl;
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}
1898E - Sofia and Strings
题意:给定两个字符串S和T,现可以对S进行操作:
1、删除S中某个字母。
2、选中S中[L,R]范围内字符,使其按照字典序大小重新升序排列。
要求若干次操作后S是否能等于T。
思路:首先通过预处理将每个字符在S中的位置全部都找出来。对于操作2而言,我们可以每次固定范围为2,那么操作2就转化成了交换相邻字符(若前者字典序大于后者)。接下来我们从前往后逐个匹配T中的字符,对于T当中的每个字符,我们尽可能的去用操作2来实现匹配,因为操作2不会删除字母,这样会为之后的字符匹配提供帮助。对于字符而言,假如说找到了S中
, 那么S中第 j 位以前的,比
小的字符在之后都是无法被找到的。因此
所在的位置必须在
之前,比它字典序大的字符的位置之后。因此每一轮需要记录一下当前字符在S中的最后匹配的位置。
// Problem: E. Sofia and Strings
// Contest: Codeforces - Codeforces Round 910 (Div. 2)
// URL: https://codeforces.com/contest/1898/problem/E
// Memory Limit: 256 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
const LL maxn = 4e05+7;
const LL N=1e05+10;
const LL mod=1e09+7;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >t;
priority_queue<LL> q;
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
int a[N];
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve()
{cin >> n >> m;string s , t;cin >> s >> t;vector<int>pos[26];for(int i = 0 ; i < n ; i ++){pos[s[i] - 'a'].pb(i);}vector<int>max_id(26 , -1);for(int i = 0 ; i < m ; i ++){int op = t[i] - 'a';int maxx = -1;for(int i = op ; i < 26 ; i ++){maxx = max(maxx , max_id[i]);}auto it = upper_bound(pos[op].begin() , pos[op].end() , maxx);if(it == pos[op].end()){cout <<"NO\n";return;}max_id[op] = *it;}cout <<"YES\n";
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}
1898F - Vova Escapes the Matrix
题意:迷宫问题,给定一个迷宫和一个起点,迷宫分为空格子和有遮挡物的格子。若从起点顺着空格子走到边缘则能够走出,接下来迷宫分为三种类型:
1、无法被走出。
2、只有一个出口能走出。
3、有两个及以上出口能走出。
接下来可以选择堵住迷宫的一些格子,但是要求堵住以后的迷宫不改变其类型,求最多能堵住多少格子。
思路:对于类型1,将迷宫中所有空格子全部堵住即可。对于类型2而言,将迷宫起点到出口最短路留下,其余全部堵住即可。最短路可以跑一边BFS求得。而对于类型3,需要保留两个出口,其余的全部都填满。即两个出口到起点的最短路保留,其余全部填满,但是需要注意的是可能两个出口到起点的最短路有重复点,需要特别处理。
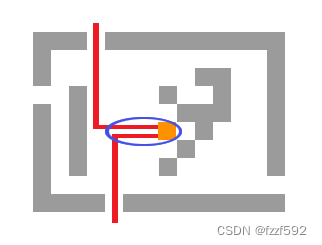
对于起点到任意一点的最短路我们可以直接一遍BFS求得,但是如何求起点到两个出口的最短路,我们可以通过逆向思维,从每个终点出发开始BFS,然后任意一个空格子可以被走过最多两次,这样能保证有两个终点走到该点上。因为是BFS,所以最先走到某个格子的两个终点必然是最短的,然后再记录一下终点到该格子的距离。最终求答案的过程我们可以遍历每一个空格子,然后假设起点到这个格子是两个最短路的重合段,用起点到该格子的距离加上两个终点到该格子的距离就是两个最短路的非重复的格子数。最后用总空格子数减去最小的非重复格子数就是答案。
// Problem: F. Vova Escapes the Matrix
// Contest: Codeforces - Codeforces Round 910 (Div. 2)
// URL: https://codeforces.com/contest/1898/problem/F
// Memory Limit: 256 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
const LL maxn = 4e05+7;
const LL N=1e05+10;
const LL mod=1e09+7;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >t;
priority_queue<LL> q;
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
int a[N];
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
int tx[4] = {0 , 1 , 0 , -1};
int ty[4] = {1 , 0 , -1 , 0};
struct Node{int x , y;int stx , sty;int d;
};
void solve()
{cin >> n >> m;string str[n + 5];queue<Node>q;//存放终点for(int i = 0 ; i < n ; i ++){cin >> str[i];}int sx = -1, sy = -1;for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {if (str[i][j] == 'V') {sx = i, sy = j;}}}vector<vector<vector<Node> > >mp(n, vector<vector<Node>>(m));auto check = [&] (int x , int y){return x >= 0 && x < n && y >= 0 && y < m && str[x][y] != '#';};auto add = [&](int x , int y){if(check(x , y)){q.push({x , y , x , y , 0}); mp[x][y].pb({x , y , x , y , 0});}};for(int i = 0 ; i < n ; i ++){add(i , 0);add(i , m - 1);}for(int i = 0 ; i < m ;i ++){add(0 , i);add(n - 1 , i);}while(!q.empty()){auto tmp = q.front();q.pop();for(int i = 0 ; i < 4; i ++){int nx = tmp.x + tx[i];int ny = tmp.y + ty[i];if(check(nx , ny)){if(mp[nx][ny].size() == 0 || (mp[nx][ny].size() == 1 && (tmp.stx != mp[nx][ny][0].stx || tmp.sty != mp[nx][ny][0].sty))){mp[nx][ny].pb({nx , ny , tmp.stx , tmp.sty , tmp.d + 1});q.push({nx , ny , tmp.stx , tmp.sty , tmp.d + 1});}}}}int ans = 0;for(int i = 0 ; i < n ; i ++){for(int j = 0 ; j < m ; j ++){if(str[i][j] == '.'){ans++;//空格子数量}}}if(mp[sx][sy].size() == 0){//无终点到达cout << ans << endl;}else if(mp[sx][sy].size() == 1){//只有1个终点能到达cout << ans - mp[sx][sy][0].d<<endl;}else{int vis[n][m];memset(vis , 0 , sizeof vis);queue<array<int,3>>q;int mi = 1e9;q.push({sx , sy , 0});vis[sx][sy] = 1;if(mp[sx][sy].size() == 2){mi = mp[sx][sy][0].d + mp[sx][sy][1].d;}while(!q.empty()){auto tmp = q.front();q.pop();for(int i = 0 ; i < 4 ; i ++){int nx = tmp[0] + tx[i];int ny = tmp[1] + ty[i];if(check(nx , ny) && !vis[nx][ny]){if(mp[nx][ny].size() == 2){mi = min(mi , mp[nx][ny][0].d + mp[nx][ny][1].d + tmp[2] + 1);}q.push({nx , ny , tmp[2] + 1});vis[nx][ny] = 1;}}}cout << ans - mi << endl;}
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}




![[python]python筛选excel表格信息并保存到另一个excel](https://img-blog.csdnimg.cn/5f78fea745a943e3a72fcb297c28ed82.png)

![【C++入门到精通】新的类功能 | 可变参数模板 C++11 [ C++入门 ]](https://img-blog.csdnimg.cn/011f2608bc4748f4b7dcf007f881967f.png)