• 本节讨论围绕这个问题展开$机器人如何观测外部世界？$

注意： 的研究的目的是为了求出点在世界坐标系下的信息，也就是$P_w$ 是要求出来的量。

1. 相机模型和内参

1. 以针孔相机为例，我们来推导内参的由来，首先在三维世界中，拍照的数学模型如下（左）：

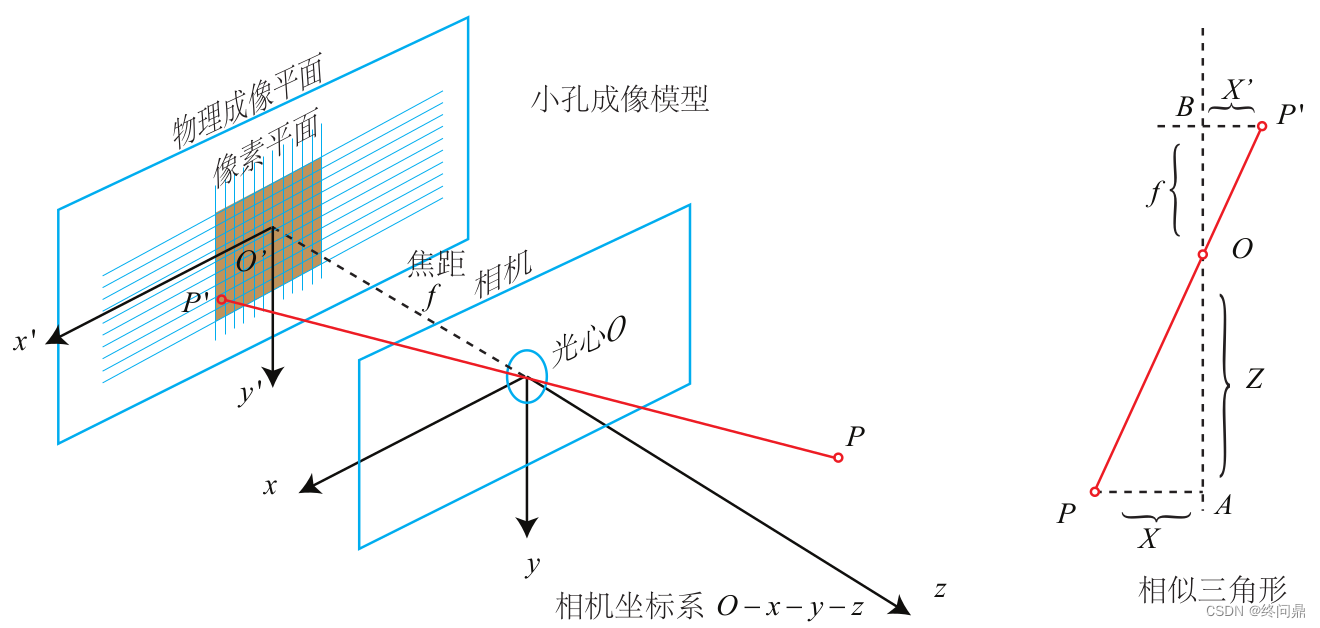
以光心为原点的一组相似三角形(对顶角的)，取它的$xoz$ 或者$yoz$ 投影上图（右）：
成像过程： 空间中一点(以相机为坐标系看)$$\begin{gathered} \mathbf{P}=[\mathbf{X},\mathbf{Y},\mathbf{Z}{]}^{\mathbf{T}} \\ ⟹ \end{gathered}$$ 投影到物理成像平面 $$\begin{gathered} {\mathbf{P}}^{\prime }=[{\mathbf{X}}^{\prime },{\mathbf{Y}}^{\prime },{\mathbf{Z}}^{\prime }{]}^{\mathbf{T}}由上图，Z^{\prime }=f(焦距) \\ ⟹ \end{gathered}$$缩放和光心平移到(像素坐标系)${{\mathbf{p}}^{\prime }=[\mathbf{u},\mathbf{v}]}^T$

1.1 内参推导

\; 本来推导出的相似三角形应该有负号(针孔模型–倒立)，但是我们选择为正(将对顶角对称到同侧(同角))，如下：

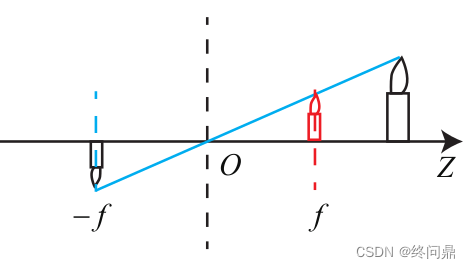
由相似关系:
$$\frac{Z}{Z^{\prime }}即\frac{Z}{f}=\frac{X}{X^{\prime }}=\frac{Y}{Y^{\prime }}$$
整理(这就是相机坐标系下点P到成像平面的步骤，对应上边第一个$⟹$)：
$$X^{\prime }=f\frac{X}{Z},Y^{\prime }=f\frac{Y}{Z}(1)$$
像素坐标系：和成像平面只差$\text{缩放}$(X缩放$\alpha$得到$u$Y缩放$\beta$得到$v$)和$\text{光心(原点)}$的平移$[c_x,c_y{]}^T$，看不懂直接看下边式子：
$$\begin{gathered} \{\begin{array}{l}u=\alpha X^{\prime }+c_x\stackrel{带入式1}{=}\alpha f\frac{X}{Z}+c_x\stackrel{记af为f_x}{=}{f}_x\frac{X}{Z}+c_x\\ v=\beta Y^{\prime }+c_y\stackrel{带入式1}{=}\beta f\frac{Y}{Z}+c_x\stackrel{记\beta f为f_y}{=}{f}_y\frac{Y}{Z}+c_y\end{array} \\ \Downarrow 写成矩阵形式如下(齐次坐标) \\ \left(\begin{array}{c}u\\ v\\ 1\end{array}\right)=\frac{1}{Z}\left(\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_x& c_y\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}X\\ Y\\ Z\end{array}\right)\triangleq \frac{1}{Z}KP \\ \Downarrow 更经常的我们会这么写 \\ Z\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)=\left(\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_x& c_y\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}X\\ Y\\ Z\end{array}\right)\triangleq KP(2) \end{gathered}$$

• 其中K就是我们常说的内参(矩阵)(Camera Intrinsics)，P还是相机坐标系下的点，Z就是点的Z坐标的值。
• 内参通常认为出厂后固定（通常不会在使用中发生变化）,有时厂商提供，有时需要自己确定内参（这一过程也称作标定）

1.2 外参推导

\quad 上边的坐标$P$ 都是在相机坐标系下进行的，而相机是运动的，所以实际中我们需要世界坐标系中的点$P_w$ 来进行这个过程。即：世界坐标$P_w$ 到相机坐标(也就是上式可用的$P$ )的变换。
\quad 这种: 变换上节介绍过,就是$P_w\stackrel{经过旋转R和平移T}{⟹}转换到P$(相机坐标系) 的过程。如下：

$$R{P}_w+t=P$$
这其中求得$R$ 和$t$就是相机的位姿，也是相机的外参(Camera Extrinsics)，带入上式(2)有

$$\begin{gathered} Z{P}_{uv}=Z\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=K(R{P}_w+t)=KT{P}_w \\ \Downarrow 齐次坐标乘以系数表达相同含义，故 \\ {P}_{uv}=KT{P}_w \end{gathered}$$
$注意:这里的P_w不再是[X,Y,Z],为了保证它和K相乘，它做一个归一化处理,P_w=[\frac{X}{Z},\frac{Y}{Z},1]$，这个点所在的平面也成为归一化平面，经过这样处理的点可以看成一个二维的其次坐标，位于$z=1$平面上，故称为归一化坐标。
\quad

下面对以上内容进行总结：

• 相机内参就是$f_x,f_y,c_x,c_y$，所以基本出厂就确定好了
• 相机外参就是$R,t$ 即相机位姿，随运动时刻变化

---

2. 畸变

2.1 径向畸变

\qquad 1. 透镜自身形状对光线传播的影响 $⟹$ 径向畸变（分为桶形畸变和枕形畸变）
\qquad 2. 这种畸变是径向对称的
\qquad 3. 将点看做极坐标下的$[r,\theta ]$ 的话，径向畸变是$r$ 发生了畸变$\delta r$。

误差随着距离中心的距离而变化，可以利用这个特性纠正：
归一化平面上的点$[x,y]$ ， 纠正完毕的点$[x_c,y_c]$,$c$ 就是$corrected$
$$\{\begin{array}{l}{x}_c=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)\\ \\ y_c=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)\end{array}$$
中心区域畸变小$k_1$ 起作用，畸变较大的用$k_2$ 起作用

2.2 切向畸变

\qquad 1. 组装过程中透镜和成像平面不完全平行 $⟹$ 切向畸变
\qquad 3. 将点看做极坐标下的$[r,\theta ]$ 的话，径向畸变是$\theta$ 发生了畸变$\delta \theta$。

切向畸变纠正如下:
$$\{\begin{array}{l}{x}_c=x+2p_{1}xy+p_2(r^2+2x^2)\\ \\ y_c=x+p_1(r^2+2y^2)+2p_{2}xy\end{array}$$

合并径向和切向畸变：
$$\begin{gathered} \{\begin{array}{l}{x}_c=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+2p_{1}xy+p_2(r^2+2x^2)\\ \\ y_c=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+p_1(r^2+2y^2)+2p_{2}xy\end{array} \\ \Downarrow 归一化平面\Rightarrow 像素平面 \\ \{\begin{array}{l}u=f_x\cdot x_c+c_x\\ v=f_y\cdot y_c+c_y\end{array} \end{gathered}$$
\quad 至此，用5个畸变项就完成了，实际中k甚至可以取一个。灵活搭配即可

3. 深度信息

\quad 上边的相机模型从光心到归一化平面连线上的所有点都可以投影到该像素(2式中的$Z$值是齐次的)。因此只有确定了P的深度，才能知道位置信息。

3.1 算法测距

1. 双目相机模型
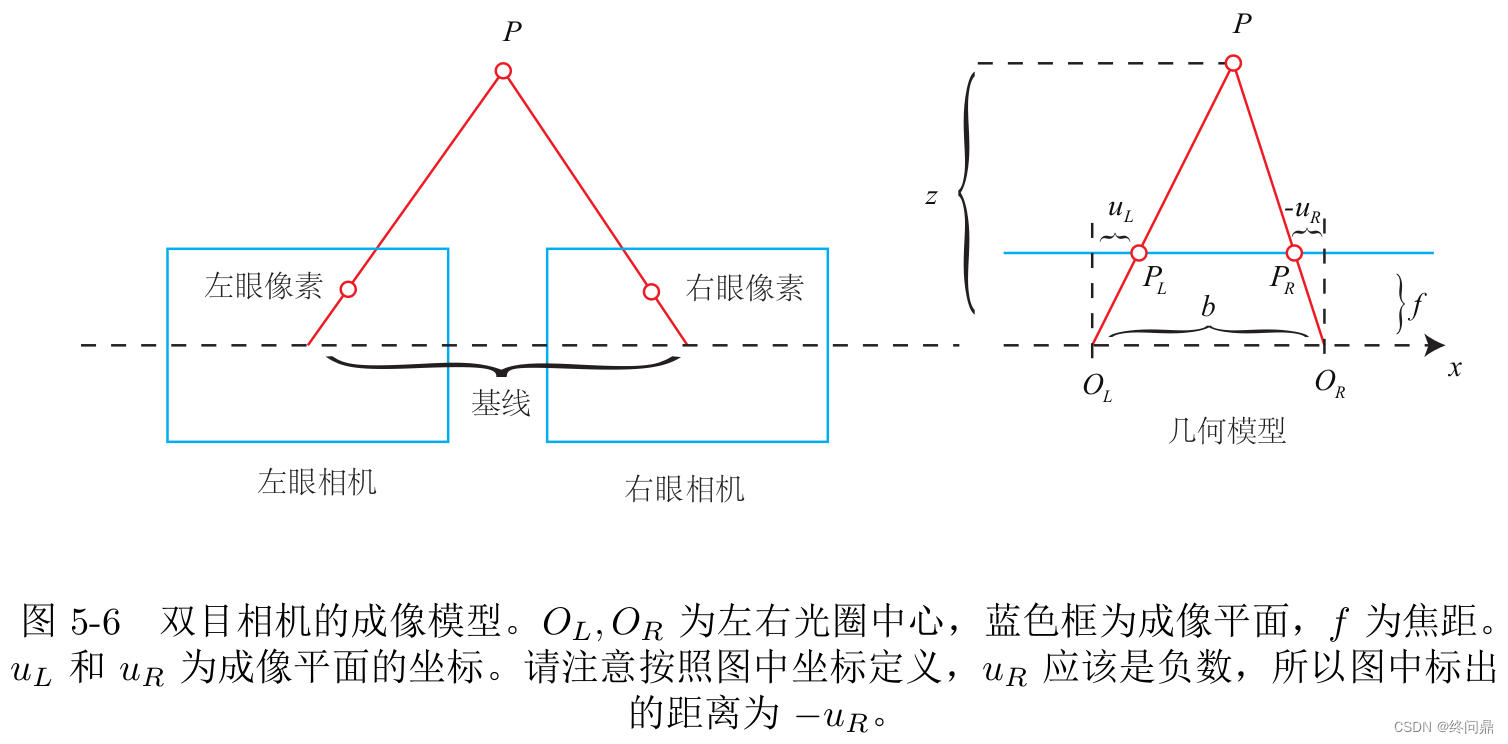   \quad 称为基线(Baseline)，按照几何模型推导
   $$\frac{z-f}{z}=\frac{b-u_L+u_R}{b}$$
   \quad 整理，$d$ 为视差:左右图横坐标之差
   $z$ 就是深度信息：

$$z=\frac{fb}{d}d=-u_L+u_R$$

• 由上式可知：视差越大，距离越近，视差越小，距离远。
• 两个相机越近(基线越小)，距离越近，反之越近。

计算量大，计算量主要用于精准定位左右眼的匹配点。

3.2 物理测距

2. RGB-D相机

• 在RGB-D深度图中，记录了每个像素距离相机的距离(单位：$mm$)，一般的量程在十几米范围左右。此外还有和普通相机一样的彩色图。