此次主要是由分类来引出

由于宝可梦的图片比较简洁,而数码宝贝的图片就显得比较复杂,我们计算出他们的轮廓,求出白色数量的多少。
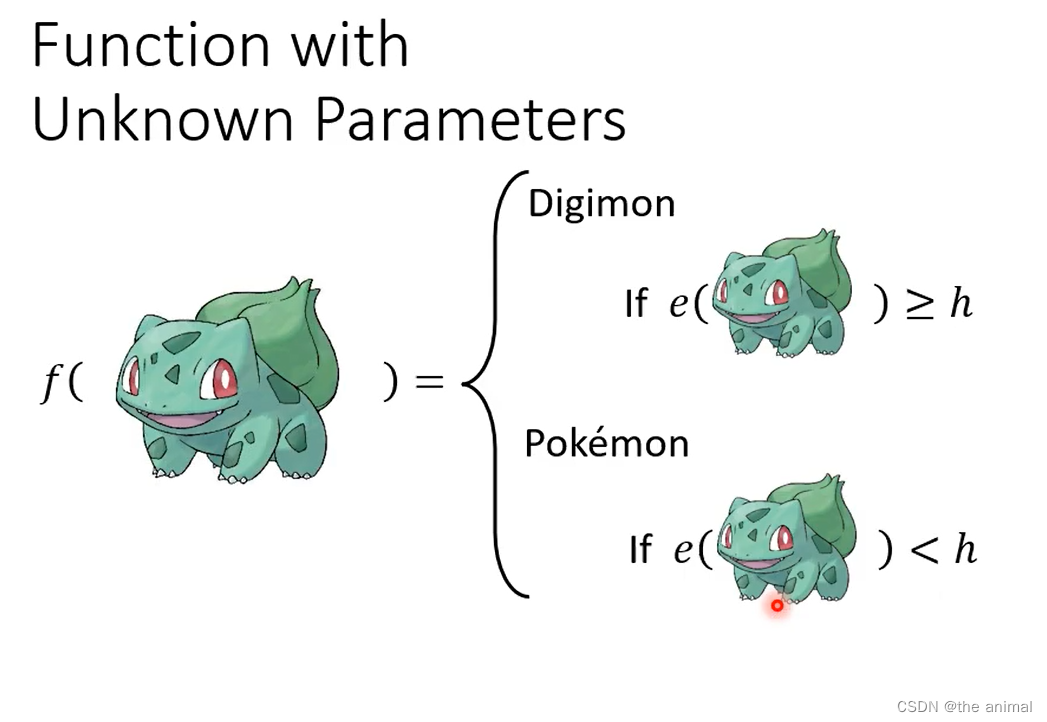
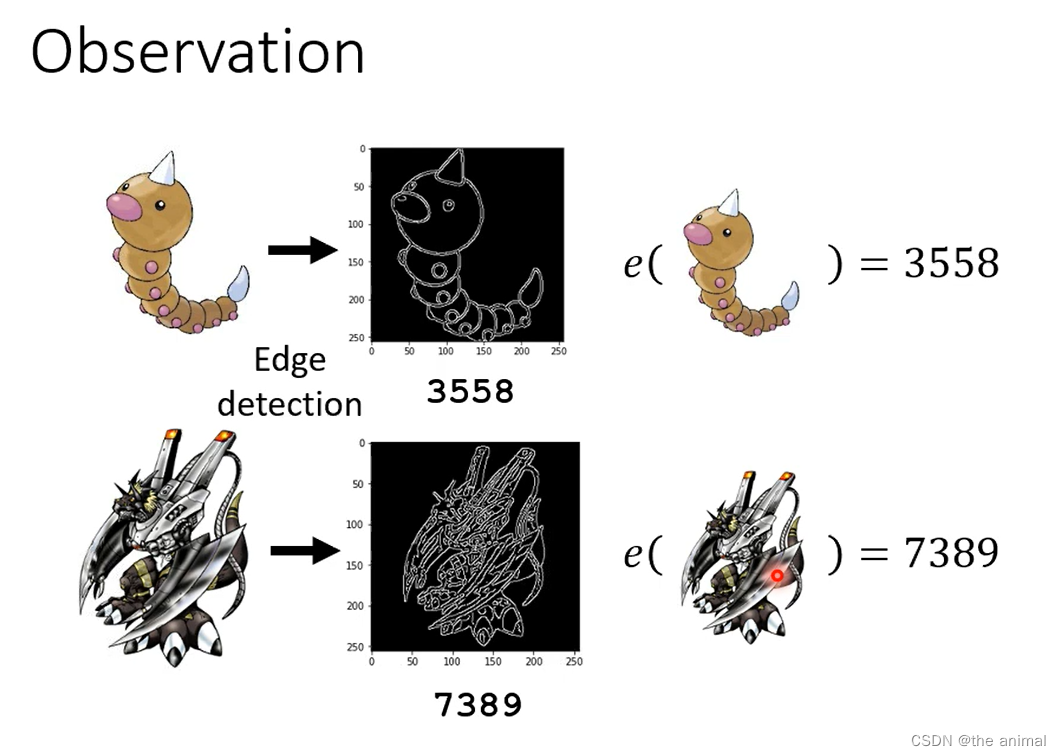 e的函数会计算线条的复杂程度。当得出的线条的复杂程度,小于h。我们认为其是宝可梦,反之就是数码宝贝。主要需要确定h的大小
e的函数会计算线条的复杂程度。当得出的线条的复杂程度,小于h。我们认为其是宝可梦,反之就是数码宝贝。主要需要确定h的大小
 以下就是H的可能大小,H的选择约多,那么模型就越复杂。也就是定义模型的参数可选择很多,也称为模型复杂程度高.
以下就是H的可能大小,H的选择约多,那么模型就越复杂。也就是定义模型的参数可选择很多,也称为模型复杂程度高.
 选择相应的loss函数。
选择相应的loss函数。
 假设全部的宝可梦和数码宝贝的数量为D_all,h_all为区别宝可梦和数码宝贝的最优临界值。D_train是我们能找到的样本数据,h_train是在我们能找的样本训练而来的临界值。
假设全部的宝可梦和数码宝贝的数量为D_all,h_all为区别宝可梦和数码宝贝的最优临界值。D_train是我们能找到的样本数据,h_train是在我们能找的样本训练而来的临界值。

以下为随机选择的样本D_train2,h_train2为由样本计算出的临界值。L(h_train2,D_all)为计算出的临界值在全部数量上的表现。
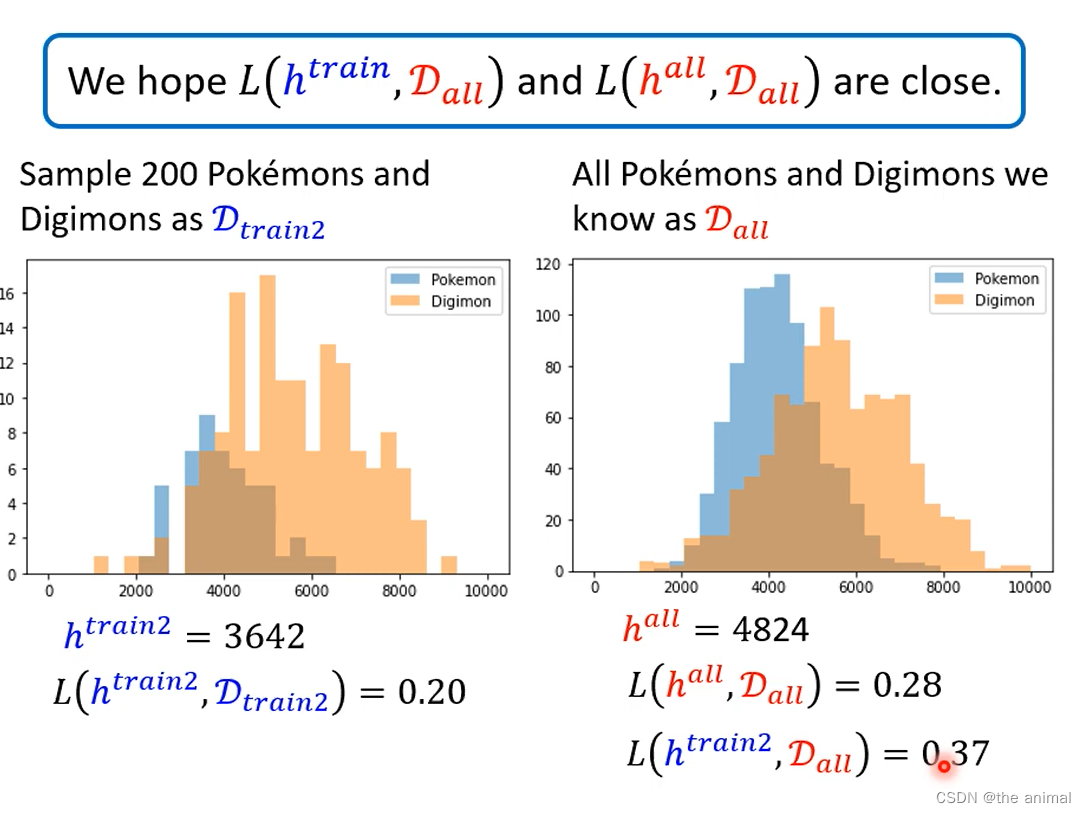
想要是什么?,我们希望同样的h在与D_train和D_all得出的loss,相差较小。所以我们需要找到一个合适的具有代表性得Data,使得在其上面训练得来的h,在全部data上面,也可以得到较好的结果。
 每一个点代表一组训练资料,像上面D_train2一样。如果D_train是坏的,那么至少有一个H,使得损失的差值大于预定的值。比如:h2会在这九个上的训练loss,会比在整体上得训练loss差值大于预设值。
每一个点代表一组训练资料,像上面D_train2一样。如果D_train是坏的,那么至少有一个H,使得损失的差值大于预定的值。比如:h2会在这九个上的训练loss,会比在整体上得训练loss差值大于预设值。

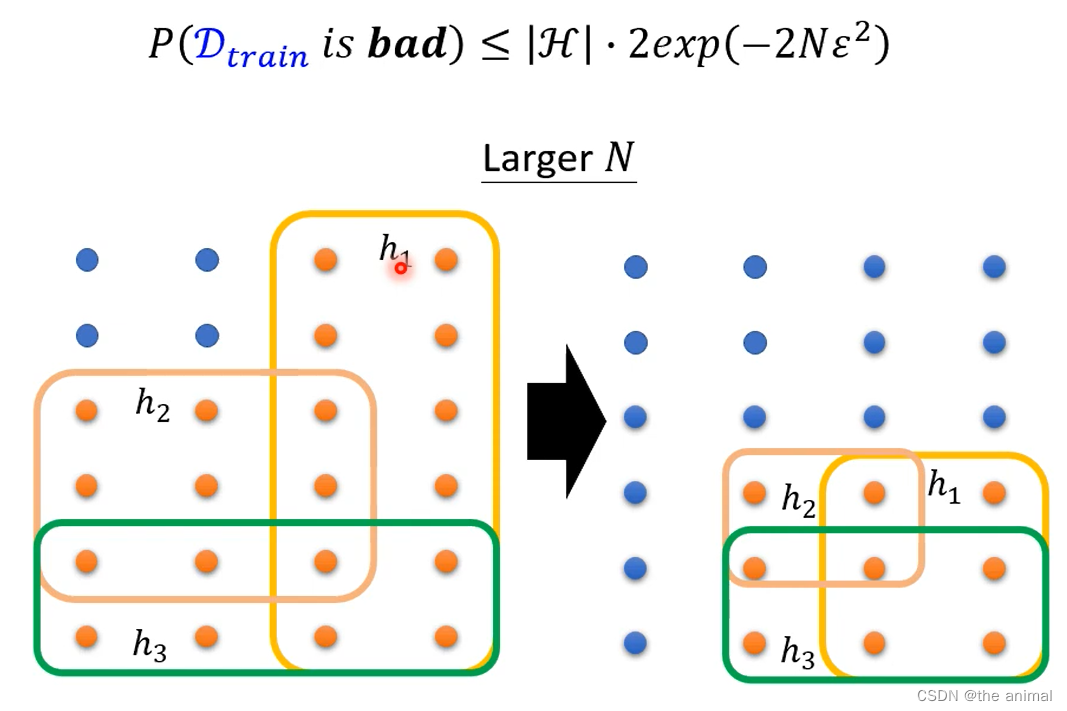
D_train是坏的样本的概率与什么有关。大N指的是样本容量 样本容量增加时 预测越精准 泛化误差上界就越趋近于零。|H|越小越好。 前者是说,训练集中实例数多了,直观看,实例越多,越接近真实分布,自然不容易得到坏模型;后者是说模型变简单了,少了一些参数,自然得到坏模型的概率就小了。
前者是说,训练集中实例数多了,直观看,实例越多,越接近真实分布,自然不容易得到坏模型;后者是说模型变简单了,少了一些参数,自然得到坏模型的概率就小了。
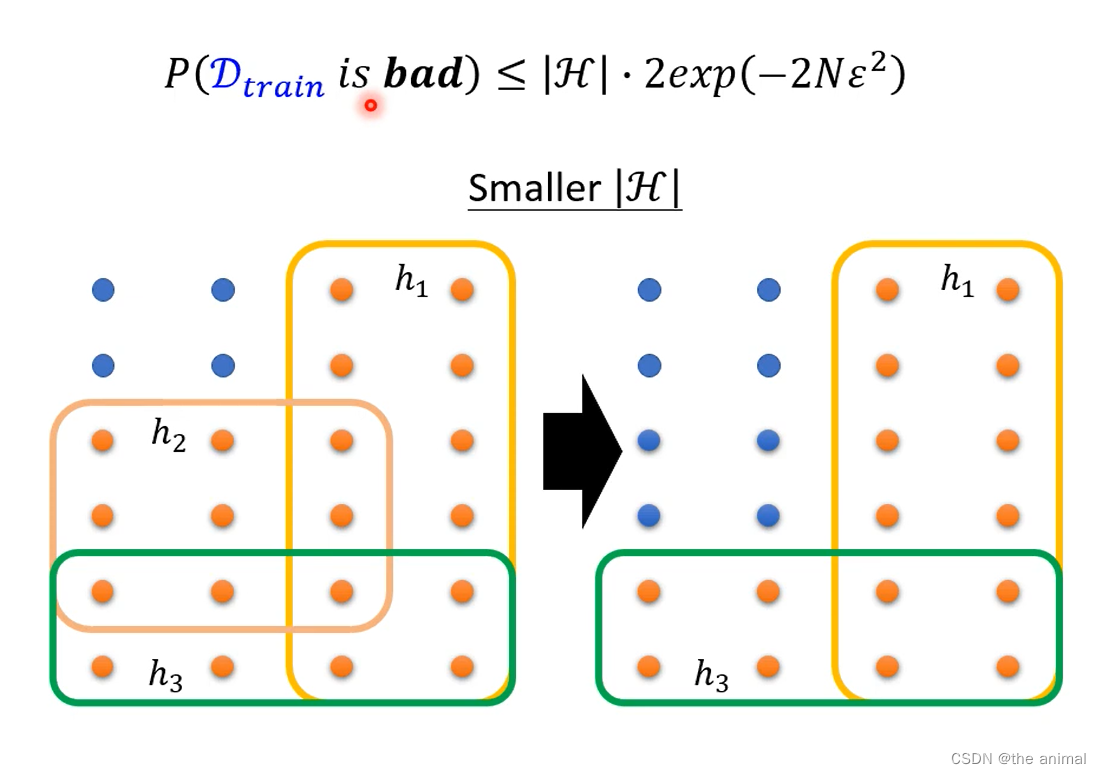
例子:


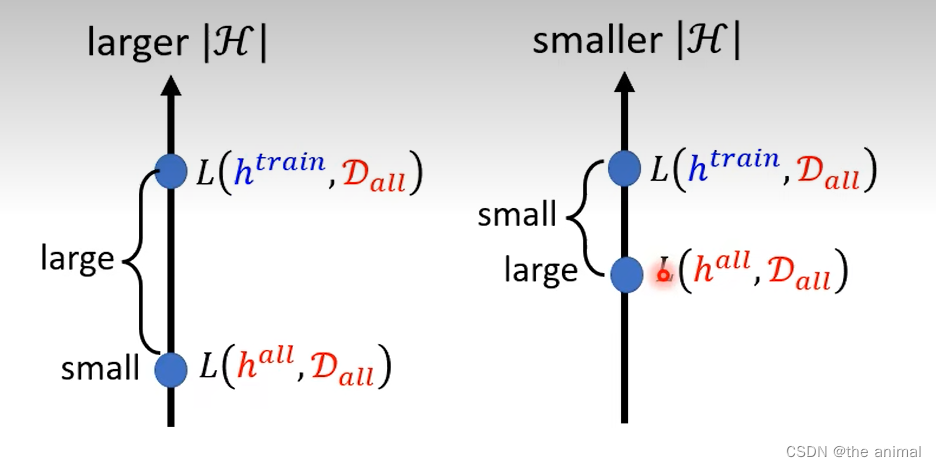
在large|H|中,理想中的L(h_all,D_all)比较小,但是现实的L(h_train,D_all)却比较大,两者相聚较远。另一种small|H|中,理想中的L(h_all,D_all)已经是比较差的,
现实的L(h_train,D_all)可以很接近。这个地方可以这样理解,相当于我们希望能在更小范围的H中找到最好的h使得Loss最小
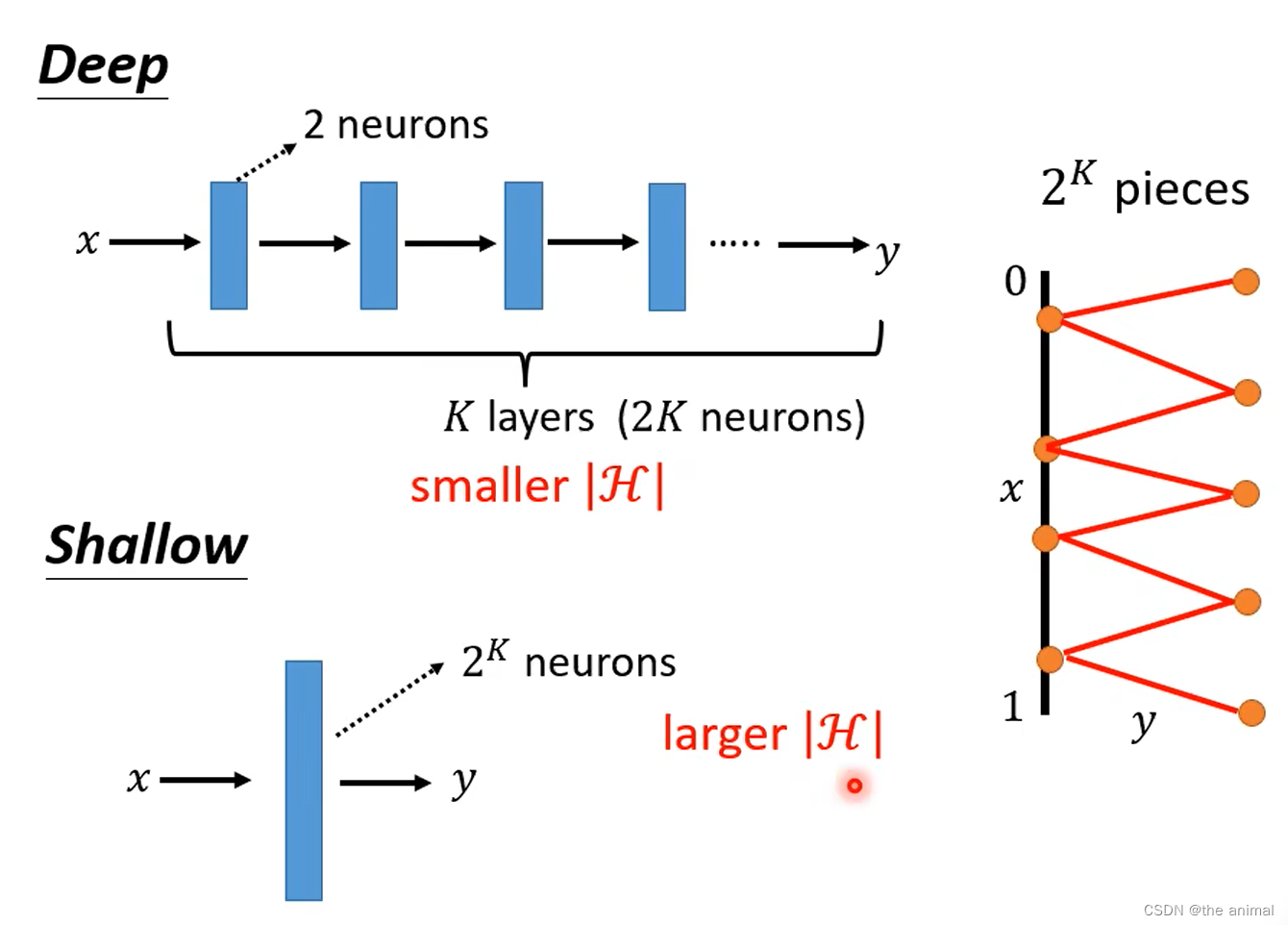
达成同一个函数,深层的网络需要的参数更少,更加不容易过拟合。Shallow因为需要的参数多,所以为了不过拟合,则需要更加多的资料。