图解系列--密钥，随机数，应用技术-编程知识

密钥

1.生成密钥
1.1.用随机数生成密钥
密码学用途的伪随机数生成器必须是专门针对密码学用途而设计的。
1.2.用口令生成密钥
一般都是将口令输入单向散列函数，然后将得到的散列值作为密钥使用。
在使用口令生成密钥时，为了防止字典攻击，需要在口令上面附加一串称为盐的随机数，然后再将其输入单向散列函数。这种方法称为“基于口令的密码” 。
1.3.更新密钥
有一种提高通信机密性的技术被称为密钥更新，这种方法就是在使用共享密钥进行通信的过程中，定期改变密钥。
在更新密钥时，发送者和接收者使用单向散列函数计算当前密钥的散列值，并将这个散列值用作新的密钥。简单说，就是用当前密钥的散列值作为下一个密钥。
1.4.保存密钥
会话密钥在通信过程中仅限使用一次，因此我们不需要保存这种密钥。然而，当密钥需要重复使用时，就必须要考虑保存密钥的问题了。
1.5.Diffie-Hellman密钥交换
使用这种算法，通信双方仅通过交换一些可以公开的信息就能够生成出共享的秘密数字，而这一秘密数字就可以被用作对称密码的密钥。实际上双方并没有真正交换密钥，而是通过计算生成出了一个相同的共享秘钥。
1.5.1.Diffie-Hellman 密钥交换的步骤
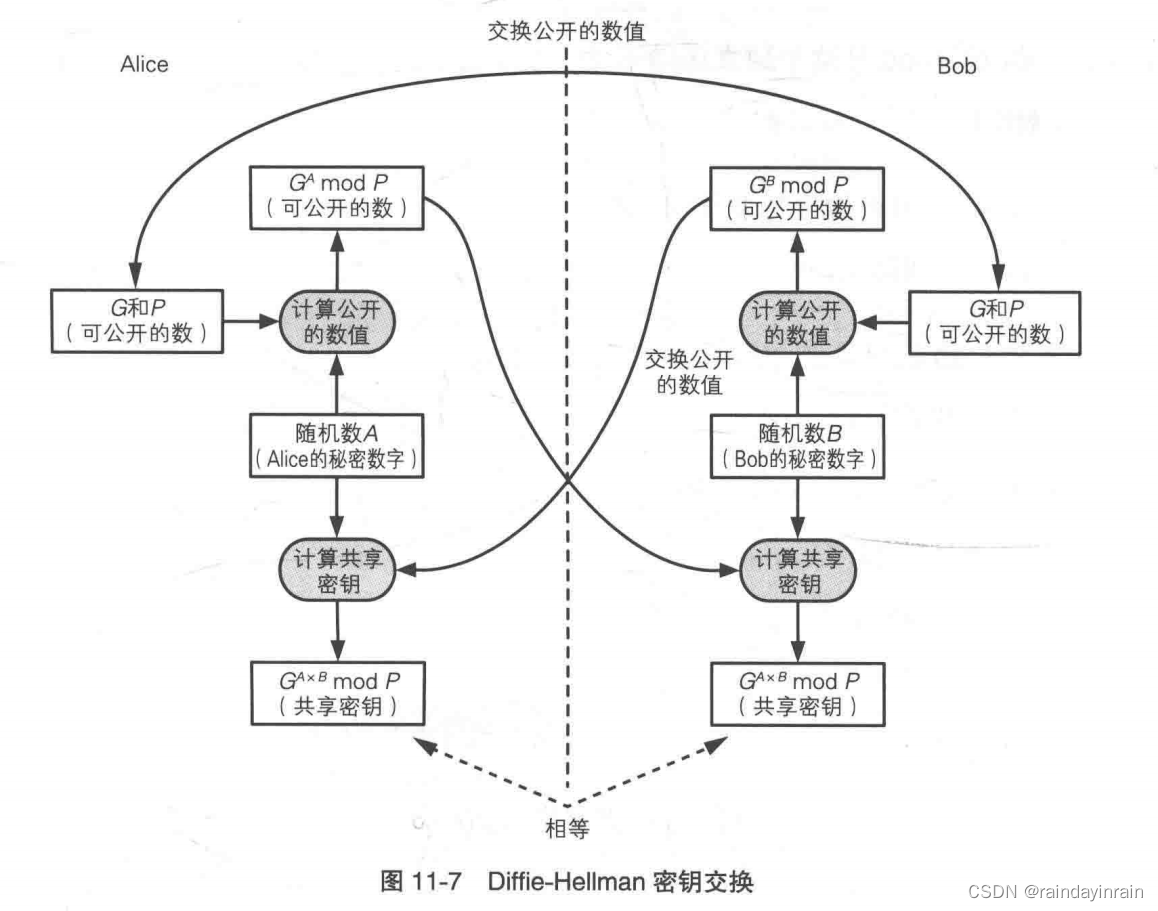
在这里插入图片描述
(1).Alice向Bob发送两个质数P和G
P必须是一个非常大的质数，而G则是一个和P相关的数，称为生成元。P和G不需要保密，被窃听者Eve获取也没关系。
(2).Alice生成一个随机数A
A 是一个1 ~ P - 2 之间的整数。这个数是一个只有Alice知道的秘密数字。
(3).Bob生成一个随机数B
B是一个1 ~ P - 2 之间的整数。这个数是一个只有Bob知道的秘密数字。
(4).Alice 将 $G^A mod P$ 这个数发送给Bob
这个数让Eve知道也没关系。
(5).Bob 将 $G^B mod P$ 这个数发送给Alice
这个数让Eve知道也没关系。
(6).Alice用Bob发过来的数计算A次方并求mod P
Alice计算的密钥= $G^B mod P)^A mod P$ = $G^{B*A}mod P)$
(7).Bob用Alice发过来的数计算B次方并求mod P
Bob计算的密钥= $G^A mod P)^B mod P$ = $G^{B*A}mod P)$

1.5.2.Eve能计算出密钥吗
在步骤(1)~(7)中，双方交换的数字(即能够被窃听者Eve知道的数字) 一共有4个： $P、 G 、G^A mod P 和 G^B mod P$ 。根据这4个数字计算出Alice和Bob的共享密钥 $G^{A×B} mod P)$ 是非常困难的。

如果仅仅是 $G^A$ 的话，要计算出A并不难，然而根据 $G^A mod P$ 计算出A 的有效算法到现在还没有出现，这个问题称为有限域的离散对数问题。而有限域的离散对数问题的复杂度正是支撑 Diffie-Hellman 密钥交换算法的基础。

1.5.3.生成元的意义
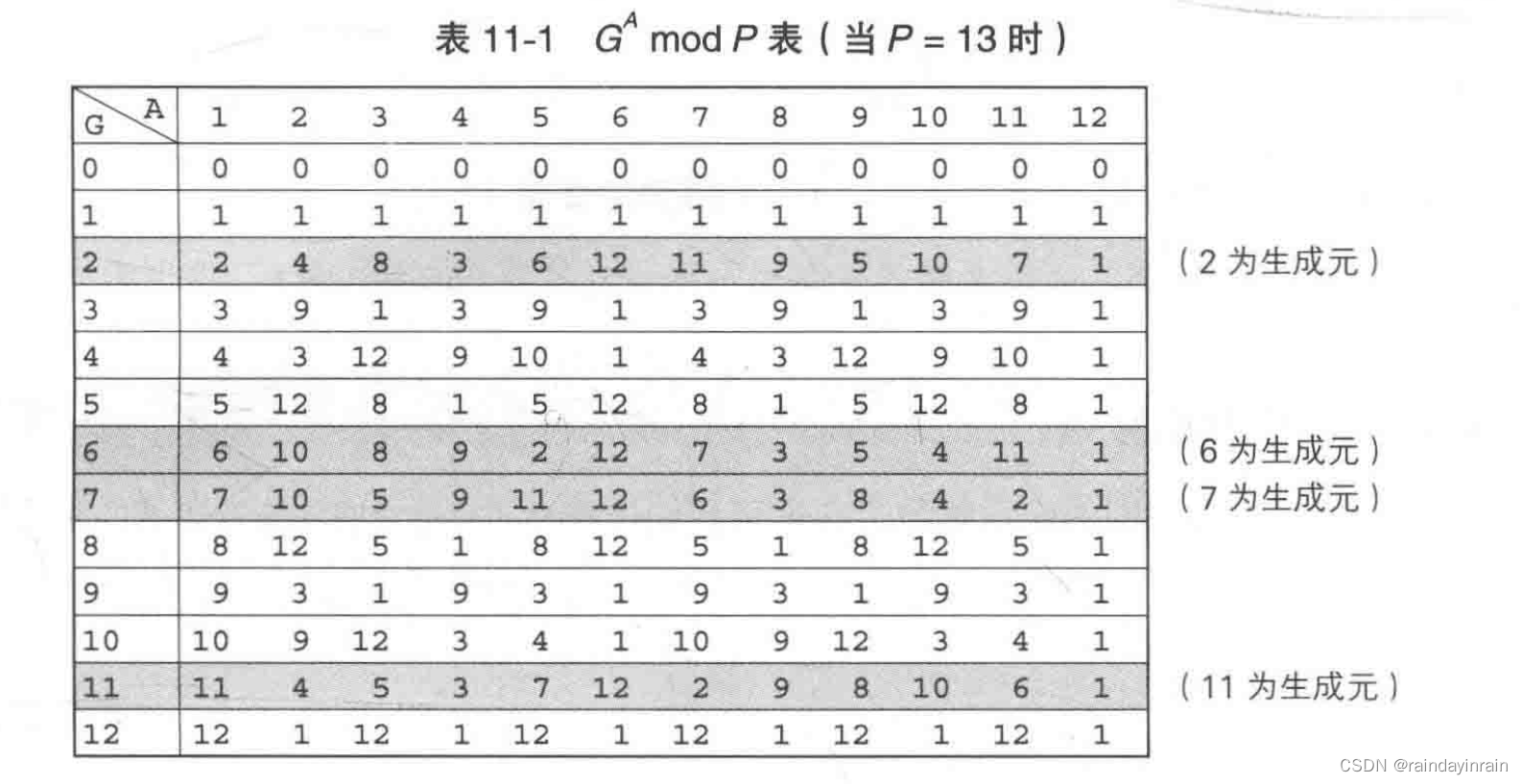
在这里插入图片描述
我们可以发现 $2^1$ 到 $2^{12}$ 的值(共12个)全都不一样。也就是说，2的乘方结果中出现了1到12的全部整数。由于2具备上述性质，因此称为13的生成元。同样地，6、7和11也是生成元。

也就是说，P的生成元的乘方结果与1 ~ P - 1 中的数字是一一对应的。正是因为具有这样一一对应的关系，Alice才能够从1~ P-2的范围中随机选择一个数字(之所以不能选择P-1，是因为 $G^{P-1} mod P$ 的值一定是等于1的)。

1.6.基于口令的密码
基于口令的密码就是一种根据口令生成密钥并用该密钥进行加密的方法。其中加密和解密使用同一个密钥。
1.6.1. PBE加密
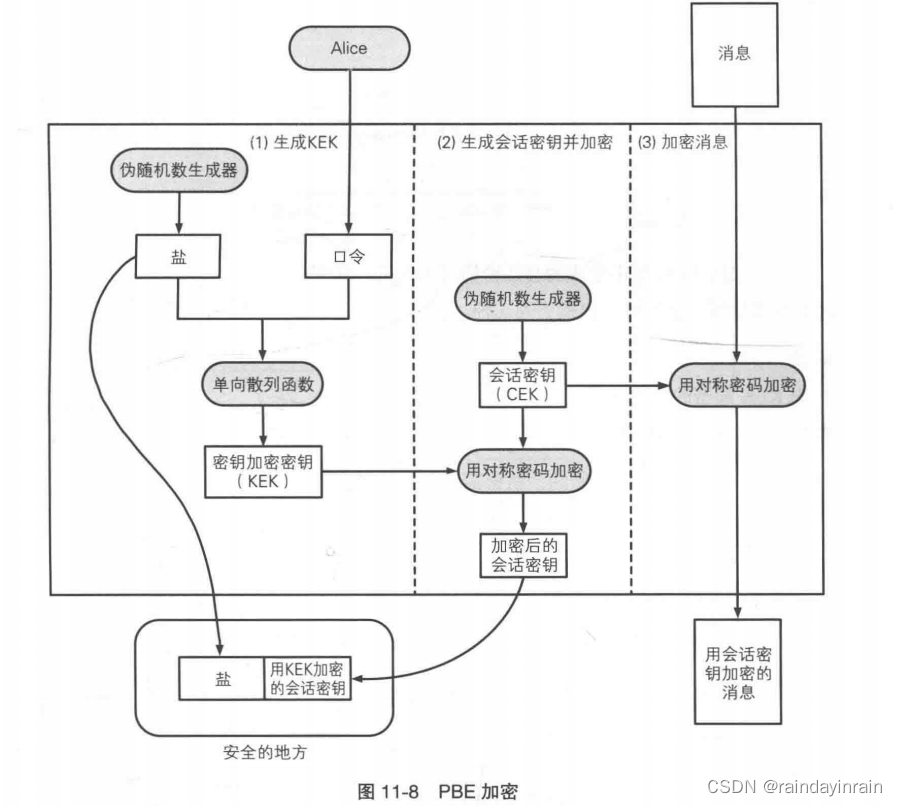
在这里插入图片描述
(1).生成KEK
首先，伪随机数生成器会生成一个被称为盐的随机数。将盐和Alice输入的口令一起输入单向散列函数，得到的散列值就是用来加密密钥的密钥(KEK)。
(2).生成会话密钥并加密
我们使用伪随机数生成器生成会话密钥。会话密钥是用来加密消息的密钥 (CEK)。
会话密钥需要用刚才步骤(1)中生成的KEK进行加密，并和盐一起保存在安全的地方。会话密钥加密之后，KEK就会被丢弃，因为KEK没有必要保存下来，只要通过盐和口令就可以重建 KEK。
(3).加密消息
(4).保存
“盐”和“用KEK加密的会话密钥”需要保存在安全的地方。

1.6.2.PBE解密
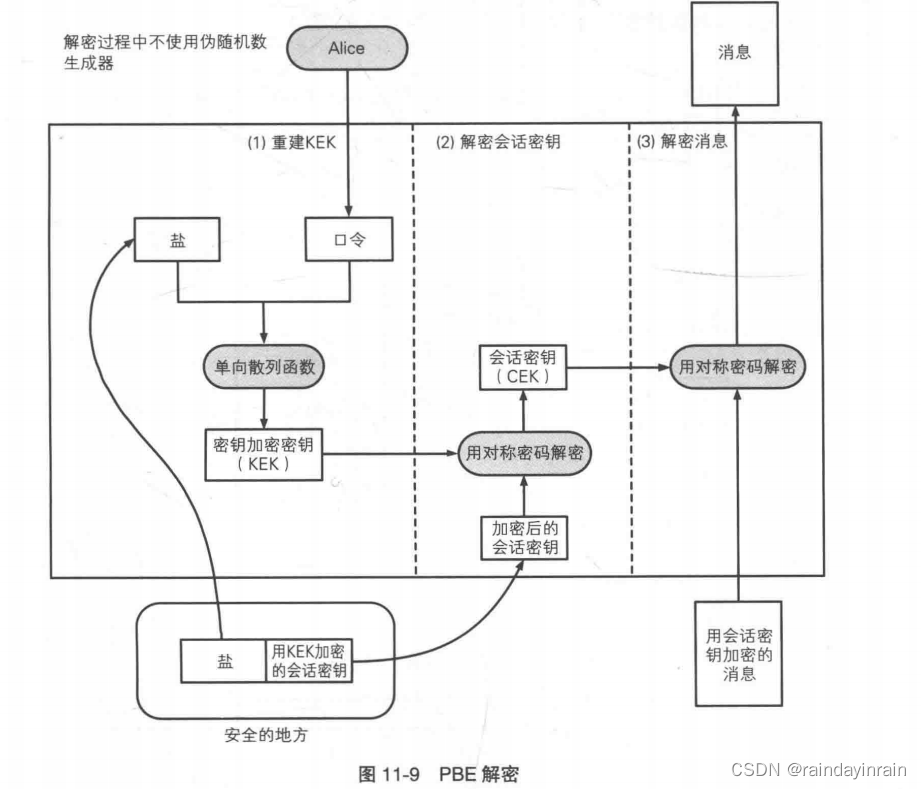
(1).重建KEK
我们将之前保存下来的盐，和Alice输入的口令一起输入单向散列函数。这个计算过程和生成 KEK时的计算过程是一样的，因此所得到的散列值就是KEK。
(2).解密会话密钥
我们获取之前保存下来的“用KEK加密的会话密钥”，用步骤(1)中恢复的KEK进行解密。这一步我们可以得到会话密钥。
(3).解密消息
在这里插入图片描述
1.6.3.盐的作用
盐是用来防御字典攻击的。字典攻击是一种事先进行计算并准备好候选密钥列表的方法。

我们假设在生成KEK的时候没有加盐。那么主动攻击者 Mallory 就可以根据字典数据（各种可能口令）事先生成大量的候选KEK。
在这里，事先是很重要的一点。这意味着Mallory可以在窃取到加密的会话密钥之前，就准备好了大量的候选KEK 。当 Mallory 窃取加密的会话密钥后，就需要尝试将它解密，这时只要利用事先生成的候选KEK，就能够大幅缩短尝试的时间，这就是字典攻击。

如果在生成KEK 时加盐，则盐的长度越大，候选KEK的数量也会随之增大，事先生成候选KEK 就会变得非常困难。加盐之后，候选KEK的数量会变得非常巨大。

1.6.4.口令的作用
在使用基于口令的密码时，需要将盐和加密后的CEK通过物理方式进行保护。例如可以将盐和加密后的CEK保存到存储卡中随身携带。

1.6.5.通过拉伸来改良PBE
将单向散列函数进行多次迭代的方法称为拉伸。

1.6.6.如何生成安全的口令
(1).使用只有自己才能知道的信息
(2).将多个不同的口令分开使用
(3).有效利用笔记
用伪随机数生成器生成一个随机的字符串作为口令，然后将口令记下来保存在安全的地方。换言之，应该将笔记与物理的钥匙同等对待。仅将口令的一部分写下来的方法也是非常有效的。
(4).理解口令的局限性
(5).使用口令生成和管理工具