2304. 网格中的最小路径代价

给你一个下标从 0 开始的整数矩阵 grid ，矩阵大小为 m x n ，由从 0 到 m * n - 1 的不同整数组成。你可以在此矩阵中，从一个单元格移动到 下一行 的任何其他单元格。如果你位于单元格 (x, y) ，且满足 x < m - 1 ，你可以移动到 (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1) 中的任何一个单元格。注意： 在最后一行中的单元格不能触发移动。

每次可能的移动都需要付出对应的代价，代价用一个下标从 0 开始的二维数组 moveCost 表示，该数组大小为 (m * n) x n ，其中 moveCost[i][j] 是从值为 i 的单元格移动到下一行第 j 列单元格的代价。从 grid 最后一行的单元格移动的代价可以忽略。

grid 一条路径的代价是：所有路径经过的单元格的 值之和 加上 所有移动的 代价之和 。从 第一行 任意单元格出发，返回到达 最后一行 任意单元格的最小路径代价。

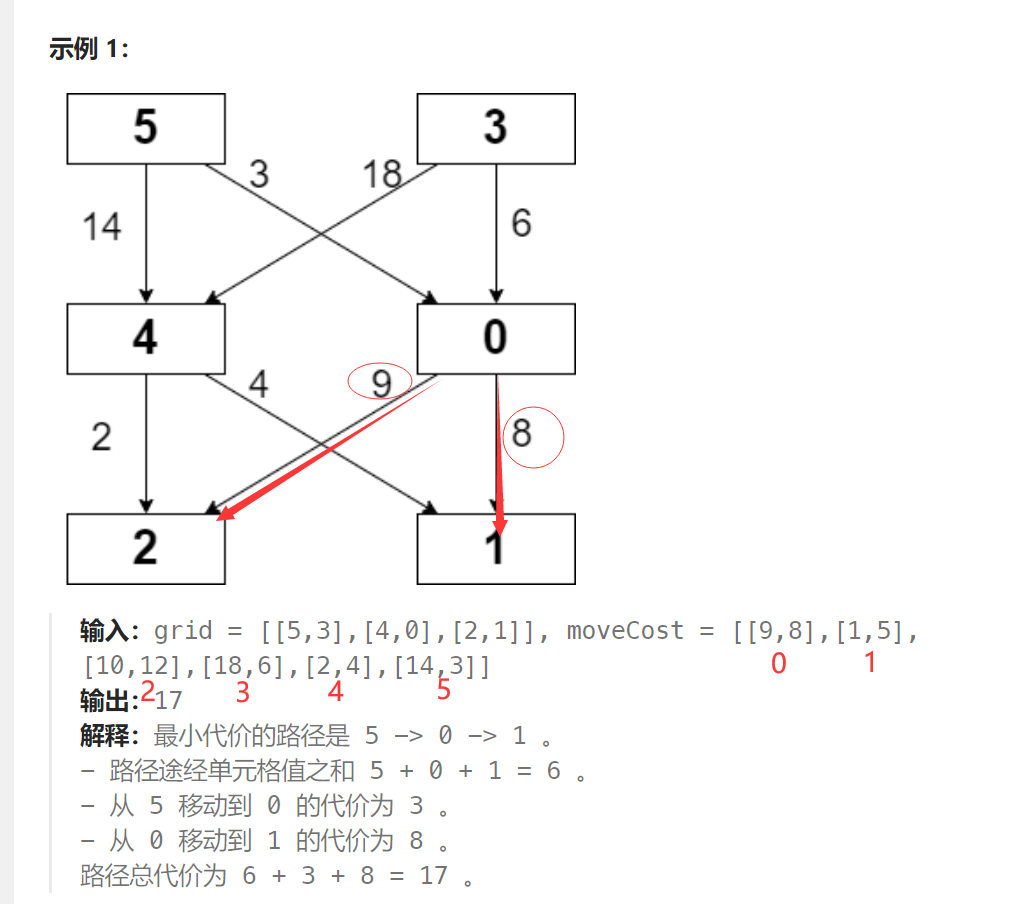
dp[i][j] 已经表示到i行j列的最小代价。

i，j的位置可以从i-1,k转移而来，所以可以得到状态转移方程：

初始条件：dp[0][j] = grid[0][j]

转移方程：dp[i][j] = min(dp[i-1][k]) + moveCost[grid[i-1][k]][j]+grid[i][j];

结果：res = min dp[m-1][j]

class Solution {
public:int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) {// dp[i][j] 已经表示到i行j列的最小代价// res = min dp[m-1][j]  // dp[0][j] = grid[0][j]// dp[i][j] = min(dp[i-1][k]) + moveCost[grid[i-1][k]][j]+grid[i][j];int m = grid.size();int n = grid[0].size();vector<vector<int>>dp(m,vector<int>(n,1000000));for(int i = 0;i<n;i++){dp[0][i] = grid[0][i];}int res=0x3f3f3f3f;for(int i=1;i<m;i++){for(int j=0;j<n;j++){for(int k=0;k<n;k++){dp[i][j]=min(dp[i][j],dp[i-1][k]+moveCost[grid[i-1][k]][j]+grid[i][j]);}}}for(int i=0;i<n;i++){res=min(res,dp[m-1][i]);}return res;}
};