python实现调和反距离空间插值法AIDW-编程知识

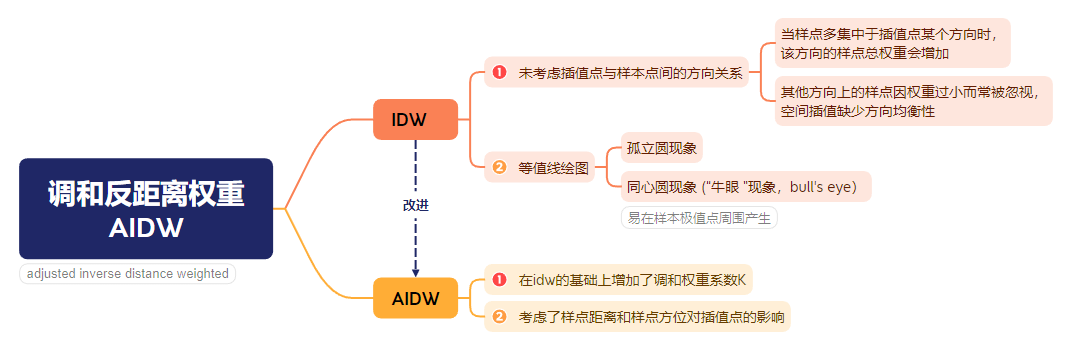
1 简介

AIDW 主要是针对 IDW 的缺点进行了改进，考虑了样本点与预测点的位置，即方向和距离，具体见下图：

在这里插入图片描述

2 改进

IDW 公式：

在这里插入图片描述

从IDW算法可看出，插值点的估算值仅与插值样本距插值点的远近相关，并未考虑样本点的方位性（即样本点被表示为各向同性）。

IDW 插值的基本假设是样点在插值区呈均匀分布。但众多情况下，样点在各向分布并非均匀，甚至会出现样点集中于某一方向的现象，违背了基本假设，其插值合理性就难被保证。针对 IDW 这一插值局限，作者提出了调和反距离权重（AIDW）插值算法。

AIDW 增加了可反映插值点与样本点方位关系的调和权重系数 K，其基本假设是：距插值点近的样本点，对其后方的样本点有遮蔽效应，当两样本点与插值点的连线夹角 $\alpha<360°/n$ （n 为插值搜索邻域内的样点个数）时，遮蔽效应存在，当 $\alpha≥360°/n$ 时，遮蔽效应消失。在 AIDW 插值过程中，受遮蔽影响的样本点，其插值权重将被削弱，削弱的程度取决于该样点 K 值的大小。

按上述假设：

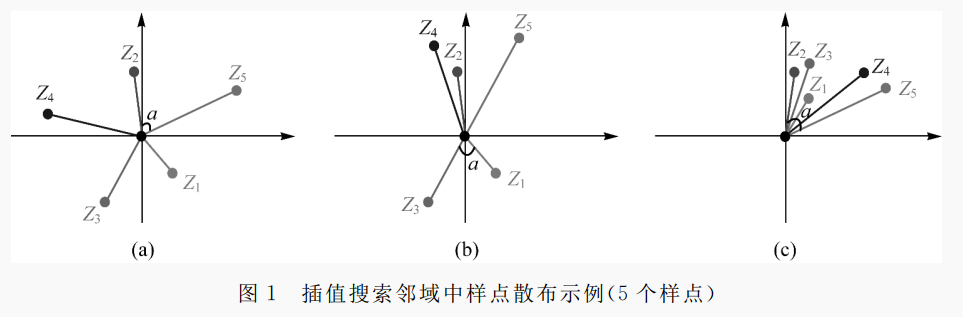
图1(a) 所示的 5 个样点在方向上均匀地分布在插值点（中心点）周围，任意两样点与插值点的连线夹角均大于或等于 72°（即α $\alpha≥360°/5$ ），即认为该５个样点间相互不存在遮蔽效应；
在图1©中，任意两样点与插值点的连线夹角均小于72°，即认为距插值点的近样点，对其后的样点均具有遮蔽效应；在大多情况下，样点在插值点周围的分布应类似图1(b)，既不像图1(a)均匀分布，也不像图1©集中分布。
图1(b)中 $Z_1$ 、 $Z_3$ 对任一样点均无遮蔽， $Z_2$ 对 $Z_4$ 、 $Z_5$ 有遮蔽， $Z_4$ 对 $Z_5$ 也有遮蔽。

在这里插入图片描述

将 IDW 传统的算法思想与本文的基本假设结合，提出了 AIDW 算法:

在这里插入图片描述

$\sin ^p\theta$ 的理解：

从下图(a)可以看出， $Z_i$ 逐渐移向 $Z_0$ 的过程种， $\theta$ 逐渐增大，当三者形成等腰三角形时， $\theta=90°$ ，此时最大，即 $\sin^p\theta=1$ ， $Z_j$ 不会对 $Z_i$ 产生遮蔽影响。
从下图(b)可以看出， $Z_i$ 保持与 $Z_0$ 相同的距离向 $Z_j$ 移动，当两者位于同一条线时， $Z_i$ 的影响完全被遮蔽，即 $\theta=0°,\sin^p\theta=0$ 。

在这里插入图片描述

计算样例：

按AIDW算法，在图3(b)中因 $Z_1$ 对 $Z_6$ 、 $Z_3$ 对 $Z_7$ 和 $Z_8$ 、 $Z_4$ 对 $Z_7$ 有遮蔽影响，这些受遮蔽样点的插值权重被削减， $Z_{10}、Z_{11}、Z_{12}$ 分别被 $Z_{4}$ 、 $Z_3$ 、 $Z_7$ 完全遮蔽，它们的插值权重降至为０。依照式(2)和式(3)，最终插值点估算值的计算式为：

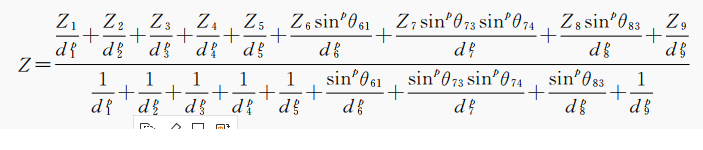
在这里插入图片描述

$Z$ 为插值点（中心点）估算值
$Z_1-Z_9$ 为样点观测值
$d_1-d_9$ 为样点与插值点的欧氏距离
p 是幂指数
$\theta$ 角如图3(b)所示

在这里插入图片描述

3 程序设计流程

AIDW 的插值程序可分为插值前准备和插值计算两个过程：

插值前准备主要是用于搜索合适的插值样点，并为下一步的插值计算提供 $d_i$ 和 $f_{ij}$ 值；
插值计算过程主要是求算反映样点遮蔽程度的 $\sin^p\theta_{ij}$ 值，并结合 $d_i、z_i$ 值求算插值点的Z值。

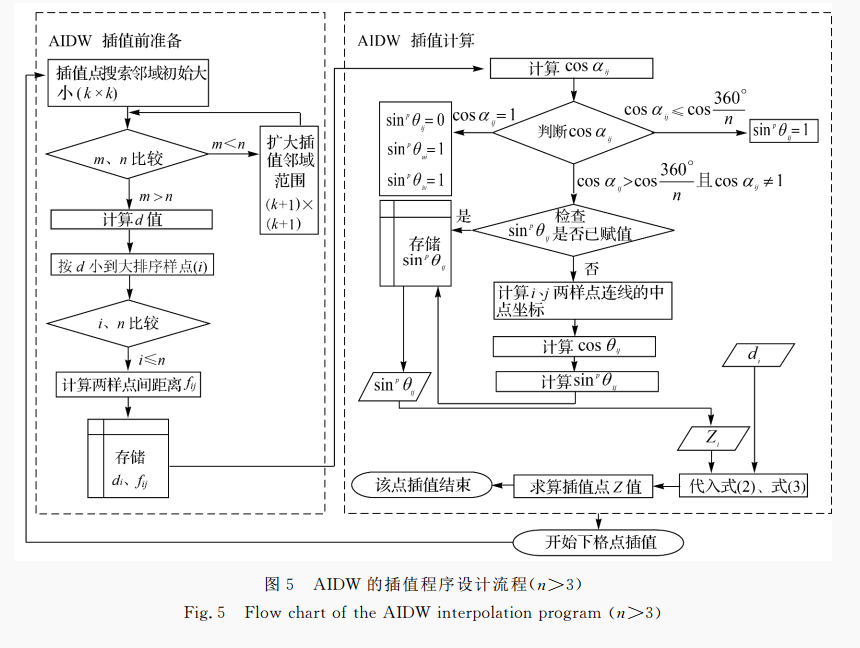
在这里插入图片描述

插值搜索邻域的大小以格点数(ｋ×ｋ)表示
m 是搜索邻域内的样点数
n 是插值所需的样点数
d、f 分别为样点与插值点的欧氏距离和两样点间的欧氏距离
i、j、u、v 均为插值样点的序号

4 插值结果

在这里插入图片描述

对比 M 点(黑色框)，IDW 出现孤立圆现象(站点集中于一侧)，AIDW 消除了孤立圆现象
对比 C 点(红色框)，IDW 出现同心圆现象，AIDW 消除了同心圆现象
对比 K 点(黄色框)，两者均出现孤立圆，通过分析，K 点周围的站点分布均匀。

从上图可以看出 AIDW 有效改进了 IDW 的缺点，同时又能保留 IDW 的插值思想，但 AIDW 需要计算 $\theta$ ，因此在插值时间上要比 IDW 慢。

5 python 实现

from sklearn.neighbors import NearestNeighbors"""类函数"""
class AIDW:def __init__(self, x, y, m,p=2):self.m = m # 搜索邻域内的样点数self.nbrs = NearestNeighbors(n_neighbors=m, algorithm='ball_tree').fit(x)self.thresh = 360/mself.p = pself.y = yself.x = xdef fit(self, x_new):indices = self.nbrs.kneighbors(x_new, return_distance=False)x_sample = self.x[indices[0]]y_sample = self.y[indices[0]]x_ = x_sample-x_newzi = []ki = 1for i in range(1, self.m-1):for j in range(i):cos_ = np.sum(x_[i]*x_[j])/((np.sum(x_[i]**2)**(1/2))*(np.sum(x_[j]**2)**(1/2)))radian = np.arccos(cos_)angle = radian*180/np.pi if angle>=self.thresh:continueelse:ki*=np.sin(radian)**self.pdi = np.sum(x_[i]**2)**(1/2)zi.append(ki/(di**self.p))z = np.sum(np.array(zi)*y_sample[1:-1])/np.sum(zi)return z"""demo"""
import numpy as np
import matplotlib.pyplot as plt# create sample points with structured scores
X1 = 10 * np.random.rand(1000, 2) -5def func(x, y):return np.sin(x**2 + y**2) / (x**2 + y**2 )z1 = func(X1[:,0], X1[:,1])# 'train'
aidw = AIDW(X1, z1, m=15)# 'test'
spacing = np.linspace(-5., 5., 100)
X2 = np.meshgrid(spacing, spacing)
grid_shape = X2[0].shape
X2 = np.reshape(X2, (2, -1)).T
z2 = []
for x2 in X2:z2.append(aidw.fit(x2.reshape(1,-1)))
z2 = np.array(z2)# plot
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, sharex=True, sharey=True, figsize=(10,3))
ax1.contourf(spacing, spacing, func(*np.meshgrid(spacing, spacing)))
ax1.set_title('Ground truth')
ax2.scatter(X1[:,0], X1[:,1], c=z1, linewidths=0)
ax2.set_title('Samples')
ax3.contourf(spacing, spacing, z2.reshape(grid_shape))
ax3.set_title('Reconstruction')
plt.show()