文章目录
- 2018 年考研管理类联考数学真题
- 一、问题求解(本大题共 5 小题,每小题 3 分,共 45 分)下列每题给出 5 个选项中,只有一个是符合要求的,请在答题卡上将所选择的字母涂黑。
- 真题(2018-01)-应用题
- 真题(2018-02)-数据描述-平均数
- 真题(2018-03)--应用题
- 真题(2018-04)-几何-平面几何
- 真题(2018-05)-代数-整式-立方差公式
- 真题(2018-06)-应用题
- 真题(2018-07)-几何-平面几何
- 真题(2018-08)-数据分析-计数原理
- 真题(2018-09)-数据分析-概率
- 真题(2018-10)-几何-解析几何
- 真题(2018-11)-数据分析-计数原理-组合
- 真题(2018-12)-概率
- 真题(2018-13)-计数原理-组合
- 真题(2018-14)-几何-立体几何
- 真题(2018-15)-代数-函数-最值函数
- 二.条件充分性判断:第 16-25 小题,每小题 3 分,共 30 分。
- 真题(2018-16)-A-几何-解析几何
- 真题(2018-17)-B-数列-等差数列
- 真题(2018-18)-D-实数
- 真题(2018-19)-D-数列-等比数列
- 真题(2018-20)-A-几何-平面几何-长方形
- 真题(2018-21)-E-方程
- 真题(2018-22)-几何-解析几何
- 真题(2018-23)-D-应用题
- 真题(2018-24)--A-几何-解析几何
- 真题(2018-25)-D-一元二次函数
2018 年考研管理类联考数学真题
一、问题求解(本大题共 5 小题,每小题 3 分,共 45 分)下列每题给出 5 个选项中,只有一个是符合要求的,请在答题卡上将所选择的字母涂黑。
真题(2018-01)-应用题
1.学科竞赛设一、二、三等奖,比例 1:3:8,获奖率 30%,已知 10 人已获一等奖,则参赛人 数 ( )
A.300
B.400
C.500
D.550
E.600
B。解析:本题考查比例相关知识。一等奖获奖人数为10人,一等奖、二等奖、三等奖获奖人数比例为1:3:8,则二等奖、三等奖获奖人数分别为30人、80人,获奖总人数为10+30+80=120人。获奖率为获奖总人数占参加竞赛总人数的比例,则参加竞赛的人数为120÷30%=400人。故本题选B。
真题(2018-02)-数据描述-平均数
2.为了解某公司员工年龄结构,按男女人数比例进行随机抽样,结果如下:
| 男员工年龄(岁) | 23 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 41 |
|---|---|---|---|---|---|---|---|---|---|
| 女员工年龄(岁) | 23 | 25 | 27 | 27 | 29 | 31 |
据表中数据统计,该公司男员工的平均年龄与全体员工平均年龄分别是( )
A.32,30
B.32,29.5
C.32,27
D.30,27
E.29.5,27
A。本题考查平均数的计算。观察男员工年龄,中间数字为32,对称位置的两个数字之和都是64(二者平均数为32),则男员工年龄的平均数为32,只有A、C两项符合。同理,可得出女员工年龄的平均数为27,则全体员工的平均年龄应大于27。故本题选A。
真题(2018-03)–应用题
3.某单位分段收费收网站流量(单位:GB)费:每日 20(含)GB 以内免,20 到 30(含) 每 GB 收 1 元,30 到 40(含)每 GB 3 元,40 以上每 GB 5 元,小王本月用了 45GB,则他该交费( )元
A.45
B.65
C.75
D.85
E.135
B。本题考查应用题中的分段收费问题。由题意可知,0到20GB(含)免费,20到30GB(含)应收费10元,30到40GB(含)应收费10×3=30元,40到50GB(含)应收费5×5=25元,则小王应交费10+30+25=65元。
真题(2018-04)-几何-平面几何
4.圆O 是△ABC 内切圆,若△ABC 面积与周长之比为 1:2,则圆O 面积( )
A.π
B.2π
C.3π
D.4π
E.5π
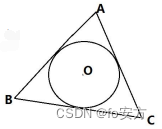
解析:本题考查三角形内切圆相关性质。如下图,M,N,P分别为切点,由于O为内切圆,则OM,ON,OP分别垂直于三角形三边,设圆O半径为r。

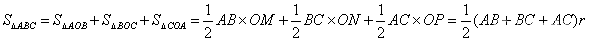
由题意,三角形ABC的面积与周长的大小之比为1:2,则可知r=1,所以圆O的面积为

真题(2018-05)-代数-整式-立方差公式
5.实数a,b 满足 ∣ a − b ∣ = 2 , ∣ a 3 − b 3 ∣ = 26 |a-b|=2,|a^3-b^3|=26 ∣a−b∣=2,∣a3−b3∣=26,则 a 2 + b 2 = a^2+b^2= a2+b2= ( )
A.30
B.22
C.15
D.13
E.10

真题(2018-06)-应用题
6.有 96 顾客至少购买了甲、乙、丙三种商品中的一种,经调查:同时购买甲、乙两种商品的有 8 位,同时购买甲、丙两种商品的有 12 位,同时购买了乙、丙两种商品的有 6 位, 同时购买了三种商品的有 2 位,则仅购买一种商品的顾客有( )位。
A.70
B.72
C.74
D.76
E.82
C。解析:本题考查容斥原理。总人数=仅购买了一种商品的人数+仅购买了两种商品的人数+购买了三种商品的人数。仅购买了两种商品的人数=仅购买了甲、乙的人数+仅购买了甲、丙的人数+仅购买了乙、丙的人数=(8-2)+(12-2)+(6-2)=20(人)。则仅购买了一种商品的人数=96-20-2=74(人)。故本题选C。
真题(2018-07)-几何-平面几何
7.四边形 A 1 B 1 C 1 D 1 A_1B_1C_1D_1 A1B1C1D1是平行四边形, A 2 B 2 C 2 D 2 A_2B_2C_2D_2 A2B2C2D2是 A 1 B 1 C 1 D 1 A_1B_1C_1D_1 A1B1C1D1四边的中点, A 3 B 3 C 3 D 3 A_3B_3C_3D_3 A3B3C3D3分别是 A 2 B 2 C 2 D 2 A_2B_2C_2D_2 A2B2C2D2四边中点,依次下去,得到四边形序列 A n B n C n D n A_nB_nC_nD_n AnBnCnDn(n = 1、2、3…) ,设 A n B n C n D n A_nB_nC_nD_n AnBnCnDn面积为 S n S_n Sn,且 S 1 = 12 S_1=12 S1=12则 S 1 + S 2 + S 3 + . . . = () S_1+S_2+S_3+...=() S1+S2+S3+...=()
A.16
B.20
C.24
D.28
E.30
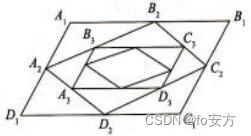

真题(2018-08)-数据分析-计数原理
8.将 6 张不同的卡片 2 张一组分别装入甲乙丙 3 个袋中,若指定的两张卡片要在同一组,则不同装法有( )种
A.12
B.18
C.24
D.30
E.36
真题(2018-09)-数据分析-概率
9.甲乙两人进行围棋比赛,约定先胜两盘者赢得比赛,已知每盘甲获胜的概率是 0.6,乙获胜的概率为 0.4,若乙在第一盘获胜,则甲赢得比赛概率为( )
A.0.144
B.0.288
C.0.36
D.0.4
E.0.6
C。解析:本题考查分步事件的概率。根据题意,甲要赢得比赛,必须连胜两盘,每盘取胜的概率都是0.6,根据乘法原理,赢得比赛的概率为0.6×0.6=0.36。故本题选C。
真题(2018-10)-几何-解析几何
10.已知圆C : x 2 + ( y − a ) 2 = b x^2+(y-a)^2=b x2+(y−a)2=b,若圆C 在点(1,2)处的切线与 y 轴交点为(0.3)则ab =( )
A.-2
B.-1
C.0
D.1
E.2

真题(2018-11)-数据分析-计数原理-组合
11.羽毛球队有 4 名男运动员和 3 名女运动员,从中选出 2 组参加混双比赛,则不同的选派方式有( )种.
A.19
B.18
C.24
D.36
E.72

真题(2018-12)-概率
12.从标号为 1 到 10 中的 10 张卡片中随机抽取 2 张,它们的标号之和能被 5 整除的概率为( )
A. 1 5 \frac{1}{5} 51
B. 1 9 \frac{1}{9} 91
C. 2 9 \frac{2}{9} 92
D. 2 15 \frac{2}{15} 152
E. 7 45 \frac{7}{45} 457

真题(2018-13)-计数原理-组合
13.某单位为检查 3 个部门的工作,由这 3 个部门主任和外聘 3 名人员组成检查组,分 2 人一组检查工作,每组有 1 名外聘成员,规定本部门主任不能检查本部门,则不同的安排方式有( )
A.6 种
B.8 种
C.12 种
D.18 种
E.36 种
C。本题考查排列组合中的错位重排。根据错位重排问题结论,3个部门主任都不检查本部门,方法总数为2.3名外聘人员分配到3个部门,全排列,方法总数为3!=6种。故不同的安排方式有2×6=12种,故本题选C。
真题(2018-14)-几何-立体几何
14.圆柱体底面半径 2,高 3,垂直于底面的平面截圆柱体所得截面为矩形 ABCD ,若弦 AB所对圆心角是 π 3 \frac{π}{3} 3π,则截去部分(较小那部分)体积为( )
A. π − 3 π-3 π−3
B. π − 6 π-6 π−6
C. π − 3 3 2 {π-3\sqrt{3}}\over2 2π−33
D. 2 π − 3 3 2π-3\sqrt{3} 2π−33
E. π − 3 π-\sqrt{3} π−3
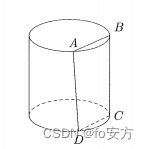

真题(2018-15)-代数-函数-最值函数
15.函数 f ( x ) = m a x f(x)=max f(x)=max{ x 2 , − x 2 + 8 x^2,-x^2+8 x2,−x2+8}的最小值为( )
A.8
B.7
C.6
D.5
E.4

二.条件充分性判断:第 16-25 小题,每小题 3 分,共 30 分。
要求判断每题给出的条件(1)和(2)能否充分支持题干所陈述的结论 A、B、C、D、E 五个选项为判断结果,请选择一项符合试题要求的判断,请在答题卡上将所选的字母涂黑。
(A)条件(1)充分,但条件(2)不充分
(B)条件(2)充分,但条件(1)不充分
(C)条件(1)和(2)都不充分,但联合起来充分
(D)条件(1)充分,条件(2)也充分
(E)条件(1)不充分,条件(2)也不充分,联合起来仍不充分
真题(2018-16)-A-几何-解析几何
16.设 x, y 为实数,则 ∣ x + y ∣ ≤ 2 |x+y|≤2 ∣x+y∣≤2
(1) x 2 + y 2 ≤ 2 x^2+y^2≤2 x2+y2≤2
(2) x y ≤ 1 xy≤1 xy≤1

真题(2018-17)-B-数列-等差数列
17.{ a n a_n an}等差数列,则能确定 a 1 + a 2 + . . . + a 9 a_1+a_2+...+a_9 a1+a2+...+a9的值.
(1)已知 a 1 a_1 a1的值
(2)已知 a 5 a_5 a5的值

真题(2018-18)-D-实数
18.设m, n 是正整数,则能确定m + n 的值.
(1) 1 m + 3 n = 1 {1\over{m}}+{3\over{n}}=1 m1+n3=1
(2) 1 m + 2 n = 1 {1\over{m}}+{2\over{n}}=1 m1+n2=1

真题(2018-19)-D-数列-等比数列
19.甲、乙、丙 3 人年收入成等比数列,则能确定乙的年收入最大值。
(1)已知甲丙两人年收入之和
(2)已知甲丙两人年收入之积

真题(2018-20)-A-几何-平面几何-长方形
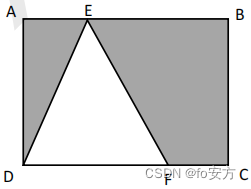
20.如图所示,在矩形 ABCD 中 AE FC .则AED 与四边形 BCFE 能拼成一个直角三角形。
(1)EB=2FC
(2)ED=EF

真题(2018-21)-E-方程
21.甲购买了若干件 A 玩具,乙购买了若干件 B 玩具送给幼儿园,甲比乙少花了 100 元,则能确定甲购买的玩具件数。
(1)甲与乙共购买了 50 件玩具
(2)A 玩具的价格是 B 玩具的 2 倍
E。本题考查方程组相关知识。假设甲的玩具价格为每件x元,共买了A件,乙的玩具价格为每件y元,共买了B件,题干前提条件为Ax+100=By,其中,x,y,A,B均为未知数。条件(1)为A+B=50 ,条件(2)为x=2y,显然,无论条件(1)、(2)单独,还是联合,未知数个数都多于方程个数,无唯一解,不能确定未知数A的值,都不充分。
真题(2018-22)-几何-解析几何
22.已知点 P ( m , 0 ) P(m,0) P(m,0), A ( 1 , 3 ) A(1,3) A(1,3), B ( 2 , 1 ) , B(2,1), B(2,1),点 ( x , y ) (x,y) (x,y)在三角形PAB 上,则 x - y 的最小值与最大值分别为-2 和1。
(1) m ≤ 1
(2) m ≥ -2

真题(2018-23)-D-应用题
23.如果甲公司年终奖总额增加 25%,乙公司年终奖总额减少 10%,两者相等,则能确定两公司的员工人数之比.
(1)甲公司的人均年终奖与乙公司相同
(2)两公司的员工数之比与两公司年终奖总额之比相等
D。本题考查比例问题。设甲公司的年终奖总额为a,乙公司的年终奖总额为b,则有a(1+25%)=b(1-10%),简化得两公司年终奖总额之比a/b=18/25,结合条件(1),可得两公司员工人数之比与奖金总额之比相等,故(1)充分,条件(2)显然充分。
秒杀:等价条件题,选项(1)是(2)充分必要条件,都选D。∵(2)甲员工/乙员工=甲年终/乙年终,得:甲年终/甲员工=乙年终/乙员工,得:甲人均年终奖=乙人均年终奖。
真题(2018-24)–A-几何-解析几何
24.设a, b 实数,则圆 x 2 + y 2 = 2 y x^2+y^2=2y x2+y2=2y与直线 x + a y = b x+ay=b x+ay=b不相交.
(1) ∣ a − b ∣ > 1 + a 2 |a-b|>\sqrt{1+a^2} ∣a−b∣>1+a2
(2) ∣ a + b ∣ > 1 + a 2 |a+b|>\sqrt{1+a^2} ∣a+b∣>1+a2

真题(2018-25)-D-一元二次函数
25.设函数 f ( x ) = x 2 + a x f(x)=x^2+ax f(x)=x2+ax ,则 f (x) 最小值与 f ( f ( x ) ) f(f(x)) f(f(x))的最小值相等.
(1) a ≥ 2
(2) a ≤ 0



2018年1月管理类联考数学参考答案
1-5 BABAE
6-10 CCBCE
11-15 DACDE
16-20 ABDAD
21-25 ECDAD