目录
- 前言
- 基础知识
- 马尔可夫决策过程 (Markov decision process, MDP)
- 回报(Return)
- 折扣回报(Discounted Return)
- State Value(状态价值函数)
- 贝尔曼方程的推导
- 贝尔曼方程的矩阵形式
- Action Value(动作价值函数)
- 贝尔曼最优公式
前言
最近在学习强化学习的内容,为了更加方便理解强化学习中的各种算法与底层原理,学习了贝尔曼方程以及最优公式,特此记录
参考课程:强化学习的数学原理
什么是贝尔曼方程?
贝尔曼方程,又叫动态规划方程,是以Richard Bellman命名的,表示动态规划问题中相邻状态关系的方程。某些决策问题可以按照时间或空间分成多个阶段,每个阶段做出决策从而使整个过程取得效果最优的多阶段决策问题,可以用动态规划方法求解。某一阶段最优决策的问题,通过贝尔曼方程转化为下一阶段最优决策的子问题,从而初始状态的最优决策可以由终状态的最优决策(一般易解)问题逐步迭代求解。存在某种形式的贝尔曼方程,是动态规划方法能得到最优解的必要条件。绝大多数可以用最优控制理论解决的问题,都可以通过构造合适的贝尔曼方程来求解。
基础知识
| 名词 | 解释 |
|---|---|
| 智能体 | 学习器与决策者的角色 |
| 环境 | 智能体之外一切组成的、与之交互的事物 |
| 动作 | 智能体的行为表征 |
| 状态 | 智能体从环境获取的信息 |
| 奖励 | 环境对于动作的反馈 |
| 策略 | 智能体根据状态进行下一步动作的函数 |
| 状态转移概率 | 智能体做出动作后进入下一状态的概率 |
RL考虑的是智能体(Agent)与环境(Environment)的交互问题:
RL的目标是找到一个最优策略,使智能体获得尽可能多的来自环境的奖励。例如赛车游戏,游戏场景是环境,赛车是智能体,赛车的位置是状态,对赛车的操作是动作,怎样操作赛车是策略,比赛得分是奖励。在论文中中常用观察(Observation)而不是环境,因为智能体不一定能得到环境的全部信息,只能得到自身周围的信息。
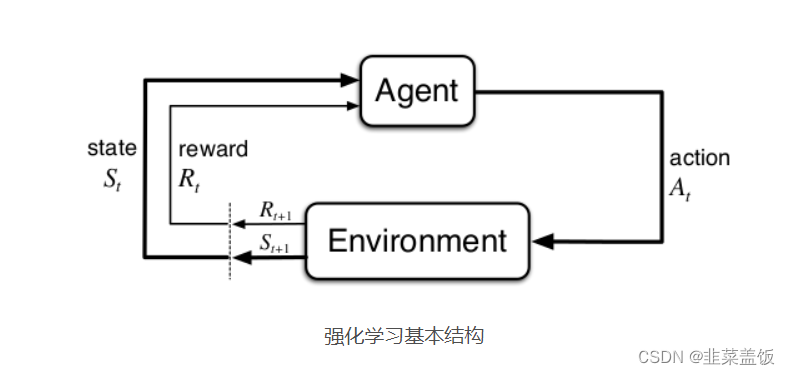
学习开始时往往采用随机策略进行实验得到一系列的状态、动作和奖励样本,算法根据样本改进策略,最大化奖励。由于奖励越来越大的特性,这种算法被称作强化学习。
马尔可夫决策过程 (Markov decision process, MDP)
强化学习的数学基础和建模工具是马尔可夫决策过程 (Markov decision process,MDP)
一个 MDP 通常由状态空间、动作空间、状态转移函数、奖励函数、折扣因子等组成。
回报(Return)
回报 (return) 是从当前时刻开始到本回合结束的所有奖励的总和,所以回报也叫做累计奖励 (cumulative future reward)。
把t时刻的回报记作随机变量 U t U_t Ut,如果一回合游戏结束,已经观测到所有奖励,那么就把回报记作 u t u_t ut ,设本回合在时刻n nn结束。定义回报为:
U t = R t + R t + 1 + R t + 2 + R t + 3 + . . . + R n U_t =R _t +R _{t+1}+R _{t+2}+R_{t+3}+...+R _n Ut=Rt+Rt+1+Rt+2+Rt+3+...+Rn
回报是未来获得的奖励总和,所以智能体的目标就是让回报尽量大,越大越好。强化学习的目标就是寻找一个策略,使得回报的期望最大化。这个策略称为最优策略 (optimum policy)。
折扣回报(Discounted Return)
在 MDP 中,通常使用折扣回报 (discounted return),给未来的奖励做折扣。折扣回报的定义如下:
G t = R t + γ R t + 1 + γ 2 R t + 2 + γ 3 R t + 3 + . . . G_t =R _t +γR _{t+1}+γ^2R _{t+2}+γ^3R_{t+3}+... Gt=Rt+γRt+1+γ2Rt+2+γ3Rt+3+...
这里的 γ ∈ [ 0 , 1 ] \gamma \in [0,1] γ∈[0,1]叫折扣率。对待越久远的未来,给奖励打的折扣越大。
t t t时刻当前状态 s t s_t st 和策略函数 π ( a ∣ s ) \pi(a|s) π(a∣s)选取动作 a t a_t at,然后状态转移 p t ( s ′ ∣ s , a ) = P ( S t + 1 ′ = s ′ ∣ S t = s , A t = a ) p_t(s'|s,a) = P(S'_{t+1}=s'|S_t=s,A_t=a) pt(s′∣s,a)=P(St+1′=s′∣St=s,At=a),选取新的状态 S t + 1 ′ = s ′ S'_{t+1}=s' St+1′=s′,奖励 R i R_i Ri只依赖于 S i S_i Si 和 A i A_i Ai
State Value(状态价值函数)
首先我们采取一个以下的过程
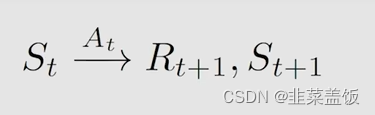
- t t t, t + 1 t+1 t+1:时间片段
- S t S_t St:在时间 t t t下的状态
- A t A_t At:在状态 S T S_T ST下采取的动作
- R t + 1 R_{t+1} Rt+1:采取动作 A t A_t At后获取到的奖励值
- S t + 1 S_{t+1} St+1:采取动作 A t A_t At后到达的状态
这样的一个动作持续下去:
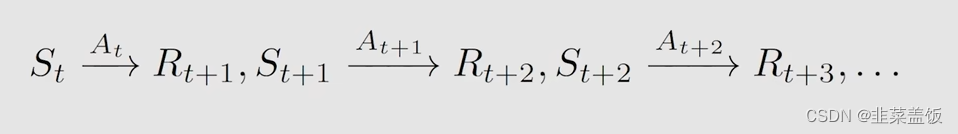
我们通过马尔可夫过程,获得一个累计的折扣奖励:
G t = R t + γ R t + 1 + γ 2 R t + 2 + γ 3 R t + 3 + . . . G_t =R _t +γR _{t+1}+γ^2R _{t+2}+γ^3R_{t+3}+... Gt=Rt+γRt+1+γ2Rt+2+γ3Rt+3+...
γ ∈ [ 0 , 1 ] \gamma \in [0,1] γ∈[0,1]
State Value是什么呢?
本质上就是 G t G_t Gt的期望,即平均值,在状态 S t S_t St下可以执行多不同的行为,从而产生多个轨迹 G t G_t Gt,State Value就是这多个 G t G_t Gt的平均值。
我们用 v π v_{\pi} vπ代表State Value
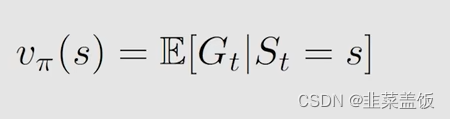
以下是采取不同策略获得的State Value
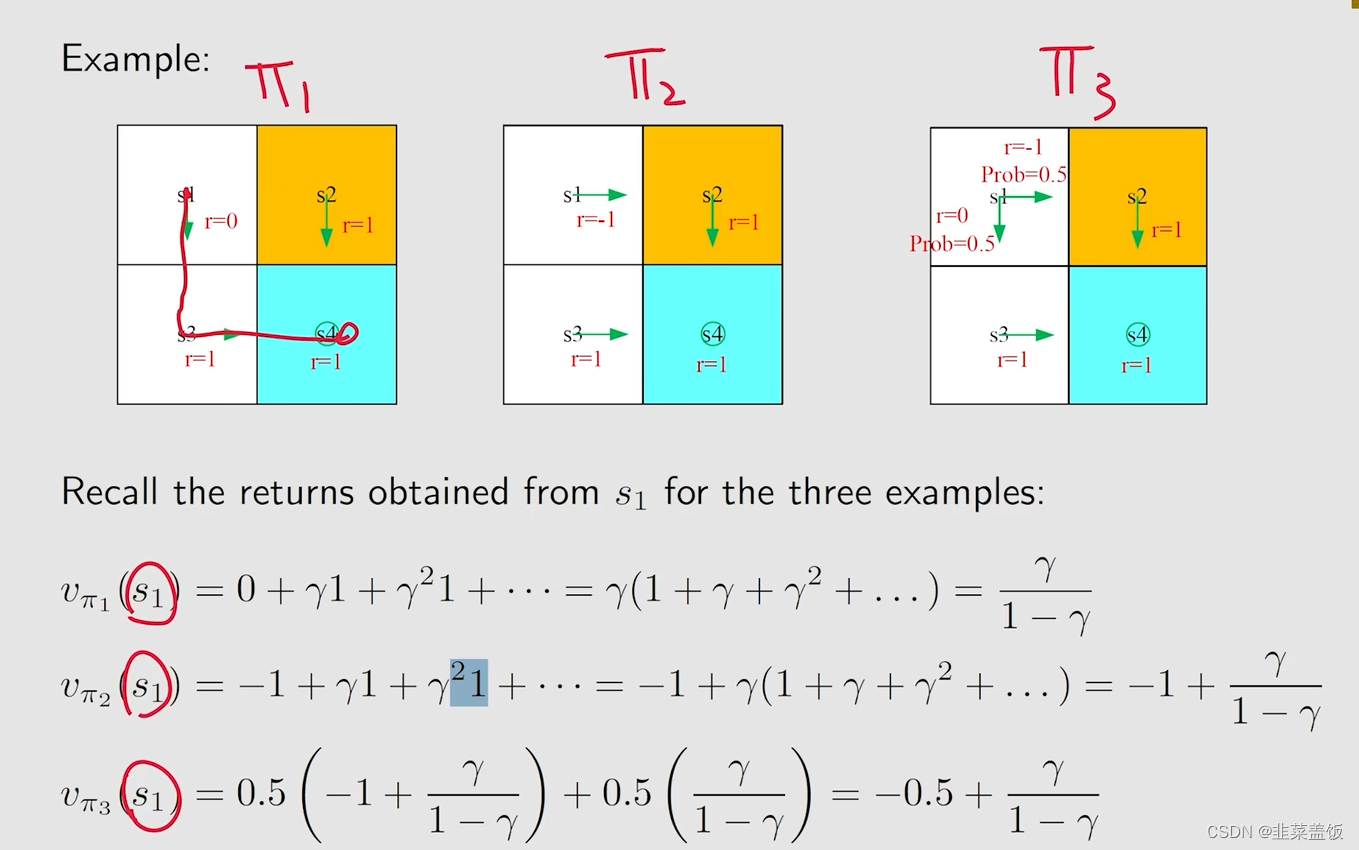
贝尔曼方程的推导
我们将上方的 G t G_t Gt的做一下修改;
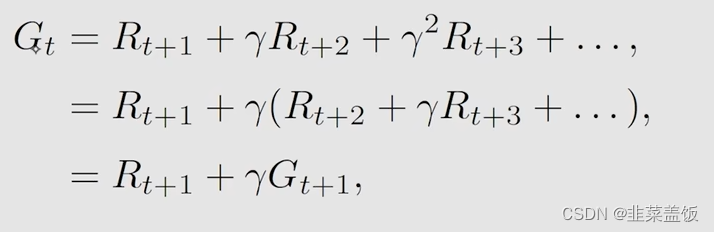
可以看到我们将 G t G_t Gt分为了两部分
然后我们将其带入到 v π ( s ) v_\pi(s) vπ(s)中,可以看到 v π ( s ) v_\pi(s) vπ(s)也被分为了两部分
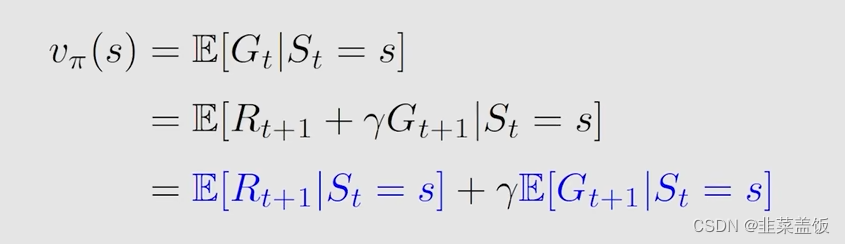
下面我们做的就是分别来分析这两个公式,就可以得到贝尔曼方程
首先第一项是 E [ R t + 1 ∣ S t = s ] E[R_{t+1} | S_t=s] E[Rt+1∣St=s]
可以得到
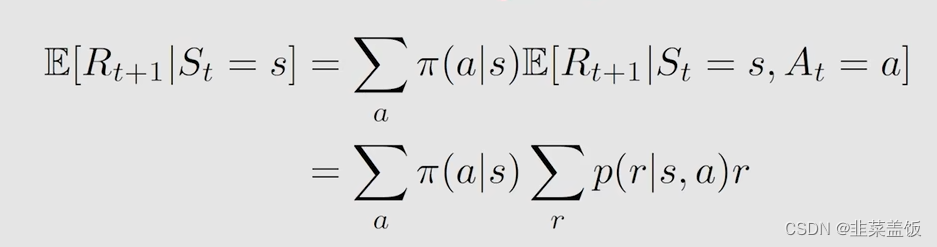
解释:在状态s可以有多个action去执行,执行a的概率为 π ( a ∣ s ) \pi(a|s) π(a∣s),然后我们在状态s下执行a,获得奖励r,我们将这多个action执行后获得的奖励求平均即可
本质上就是我们在状态s下执行各种action获得奖励的平均值,为及时奖励
我们再来看第二项
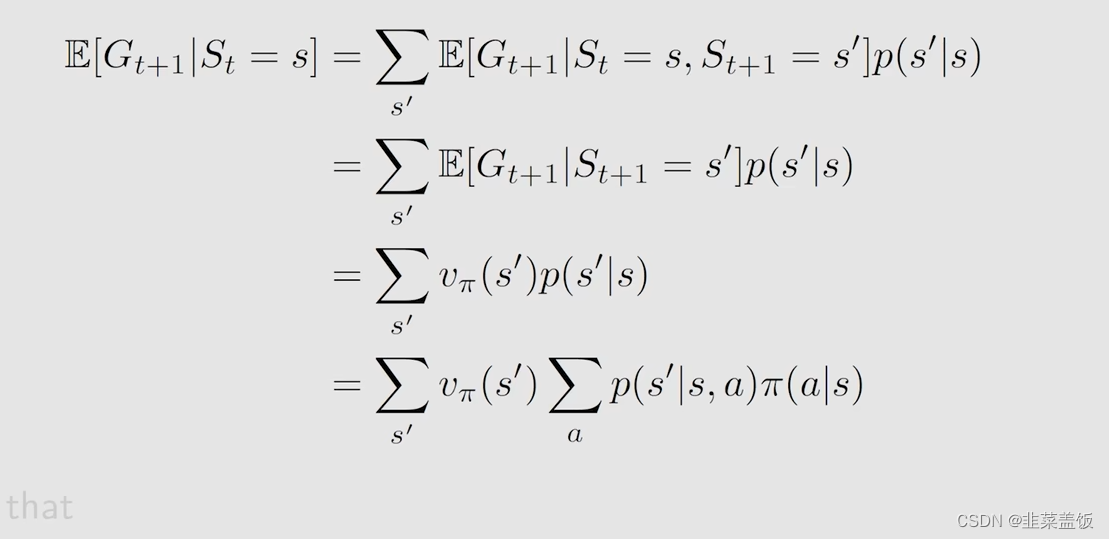
解释:通过马尔可夫的性质:下个状态只与当前状态信息有关,与更早之前的状态无关,即“无记忆性”,我们可以省去 S t = s S_t=s St=s,因为 E [ G t + 1 ∣ S t + 1 = s ‘ ] E[G_{t+1} | S_{t+1}=s^‘] E[Gt+1∣St+1=s‘]就是下一个状态的 v π v_{\pi} vπ,所以可以推导出以上公式
本质上是未来奖励
推导完上面的两项公式,我们将推导的公式代入到 v π v_{\pi} vπ,就可以得出贝尔曼方程:
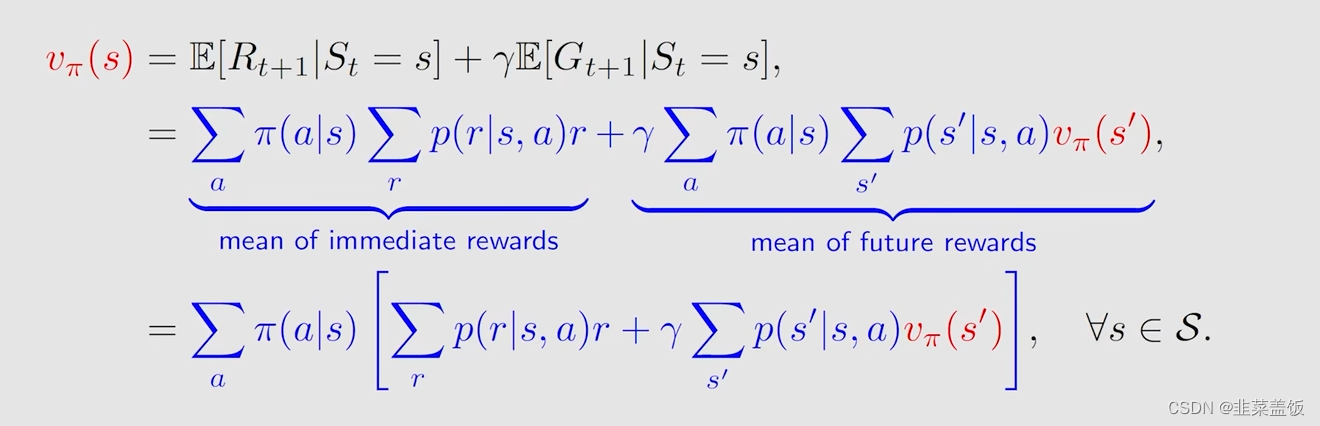
这个公式描述了不同状态之间的关系,因为左边是 v π ( s ) v_{\pi}(s) vπ(s),右边是 v π ( s ’ ) v_{\pi}(s^’) vπ(s’)
例子:
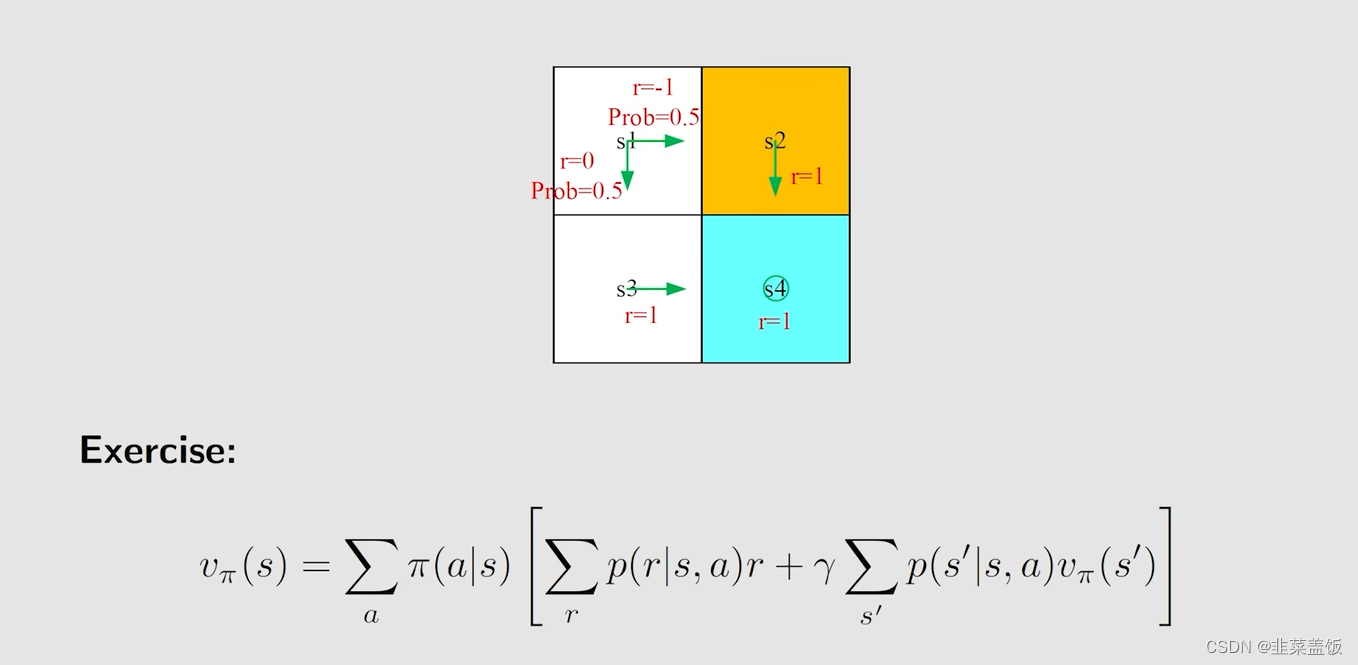
我们从 s 1 s_1 s1出发,根据贝尔曼方程,我们可以得到
v π ( s 1 ) v_{\pi}(s_1) vπ(s1) = 0.5[0+γ v π ( s 3 ) + 0.5 [ − 1 + γ v π ( s 2 ) ] v_{\pi}(s_3)+0.5[-1+γv_{\pi}(s_2)] vπ(s3)+0.5[−1+γvπ(s2)]
从 s 2 s_2 s2、 s 3 s_3 s3、 s 4 s_4 s4,分别可以得到:
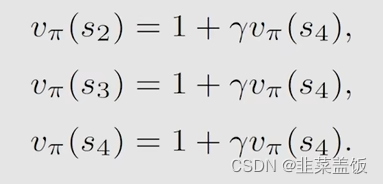
贝尔曼方程的矩阵形式
当我们有了一个贝尔曼方程,我们需要求解该贝尔曼方程
对于贝尔曼方程,所有的状态都是适用的,这样我们可以写成一个矩阵的形式,这样方便我们去求解该方程。
我们先令以下公式成立:
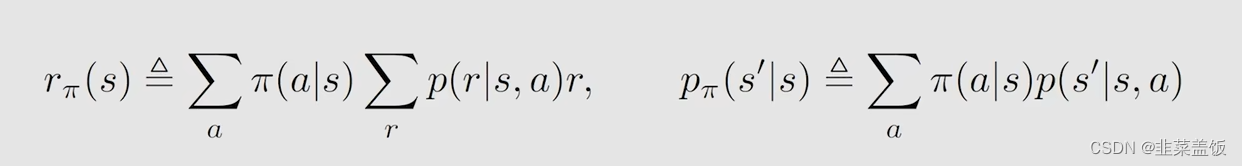
然后我们就可以将贝尔曼方程,化简为:
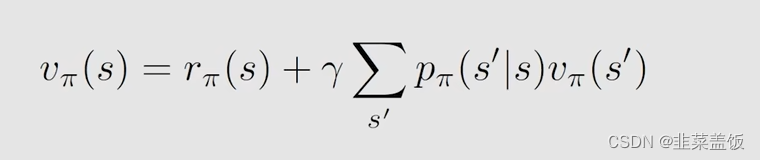
我们将其化为矩阵形式就需要多个状态,我们设有n个状态:

从刚才的公式我们可以得到:
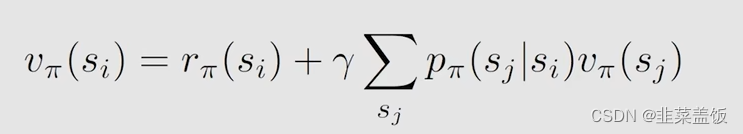
然后我们令:
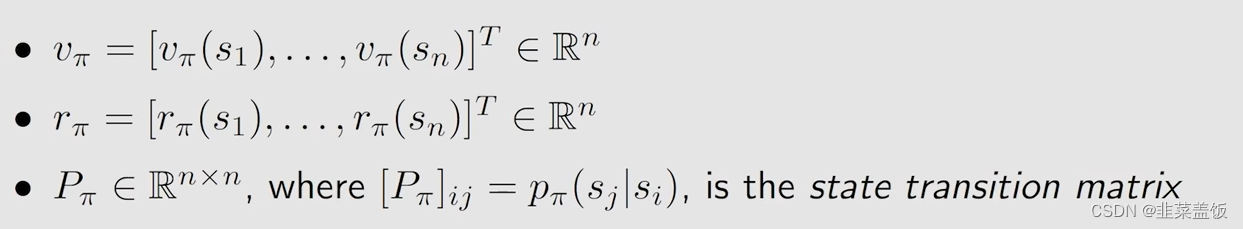
[ P π ] i j [P_\pi]_{ij} [Pπ]ij代表第i行第j列的元素是从 s i s_i si跳到 s j s_j sj的这样一个概率
之后我们就可以得到,贝尔曼方程的矩阵形式如下:
v π = r π + γ P π v_\pi = r_\pi + γP_\pi vπ=rπ+γPπ v π v_\pi vπ
具体例子如下:
例子1:
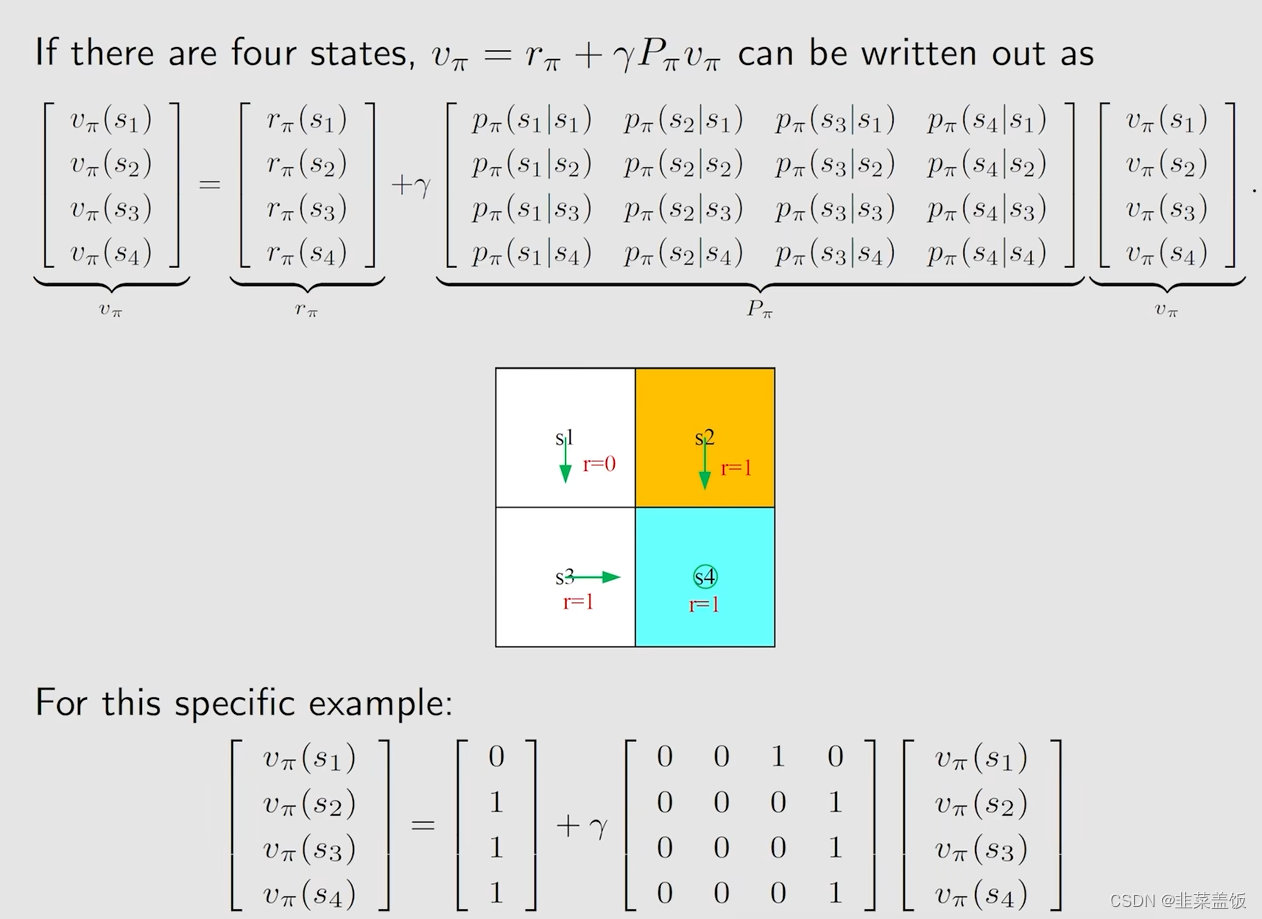
例子2:
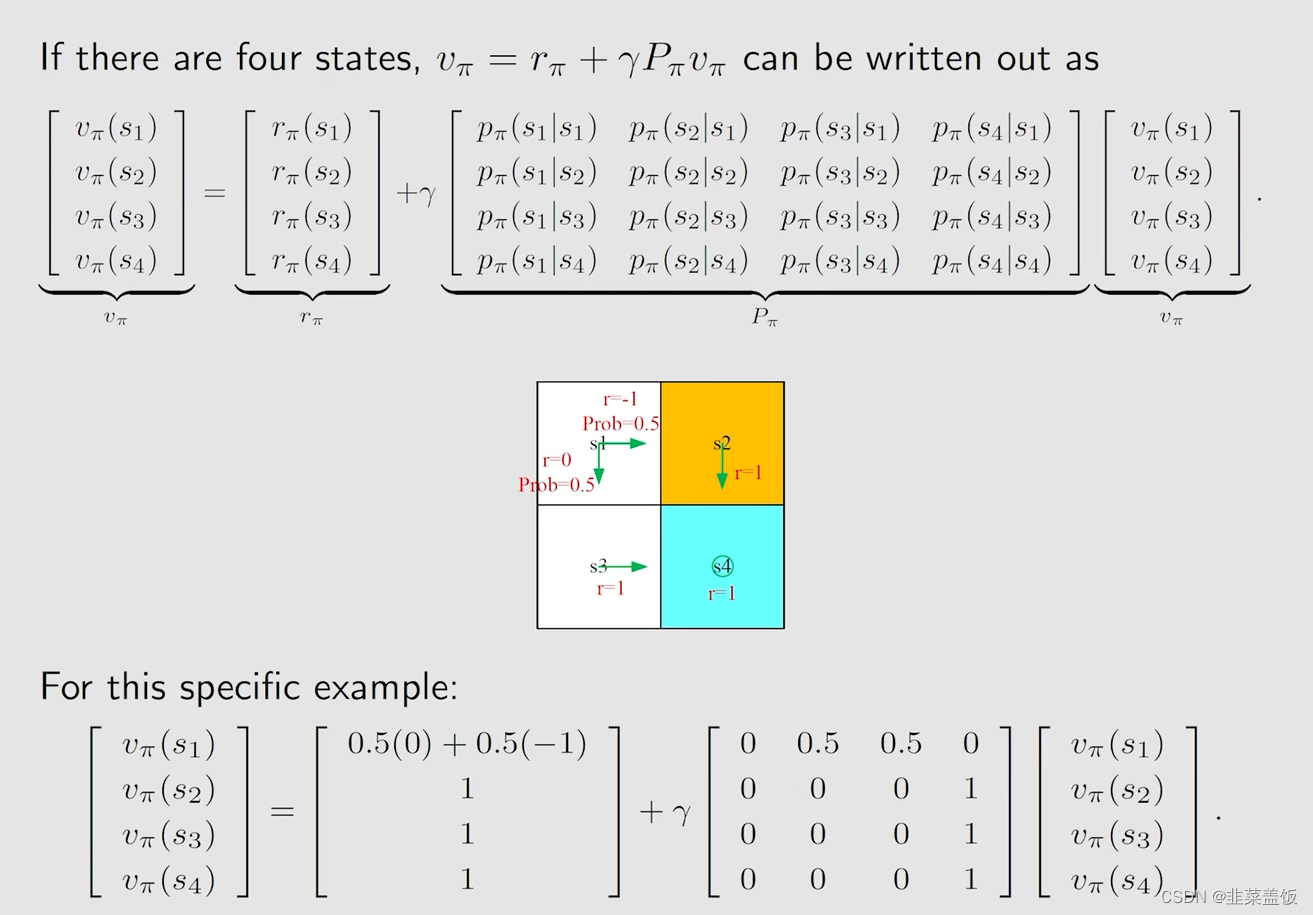
我们如何求解这个矩阵形式的贝尔曼方程呢?
可以使用迭代的方式去求解
通过 v 0 v_0 v0求出 v 1 v_1 v1,通过 v 1 v_1 v1求出 v 2 v_2 v2,以此迭代下去。
Action Value(动作价值函数)
- State value:从一个状态s出发得到的平均奖励(从状态s出发的多条轨迹的平均奖励)
- Action vlaue:从一个状态出发并选择一个action得到的平均奖励
Action value的定义如下:
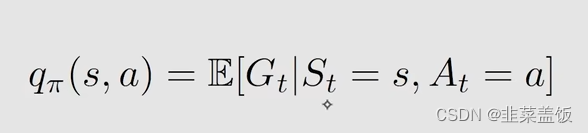
我们从数学上看一下 Action value与State value的关系:
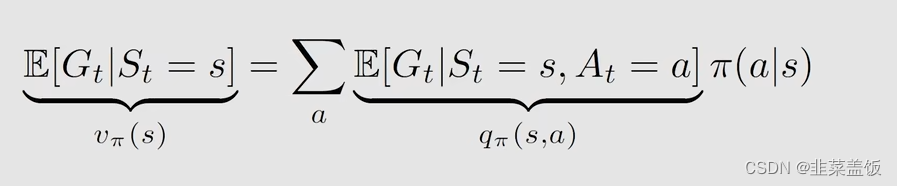
因此
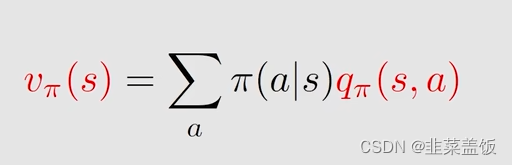
我们将上面这个公式与下面的公式做对比
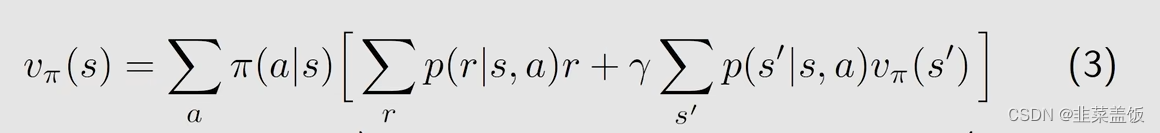
我们可以得到画线的就是Action value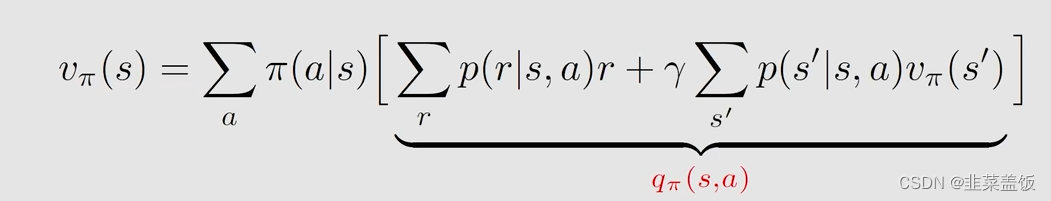
即
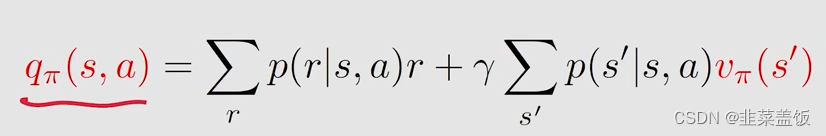
所以我们可以得出结论:
- 1、如果我们得到一个状态s下的所有Action value,求平均就可以得到State value
- 2、如果我们得到所有状态的State value,就可以得到所有的Action value
具体例子如下:
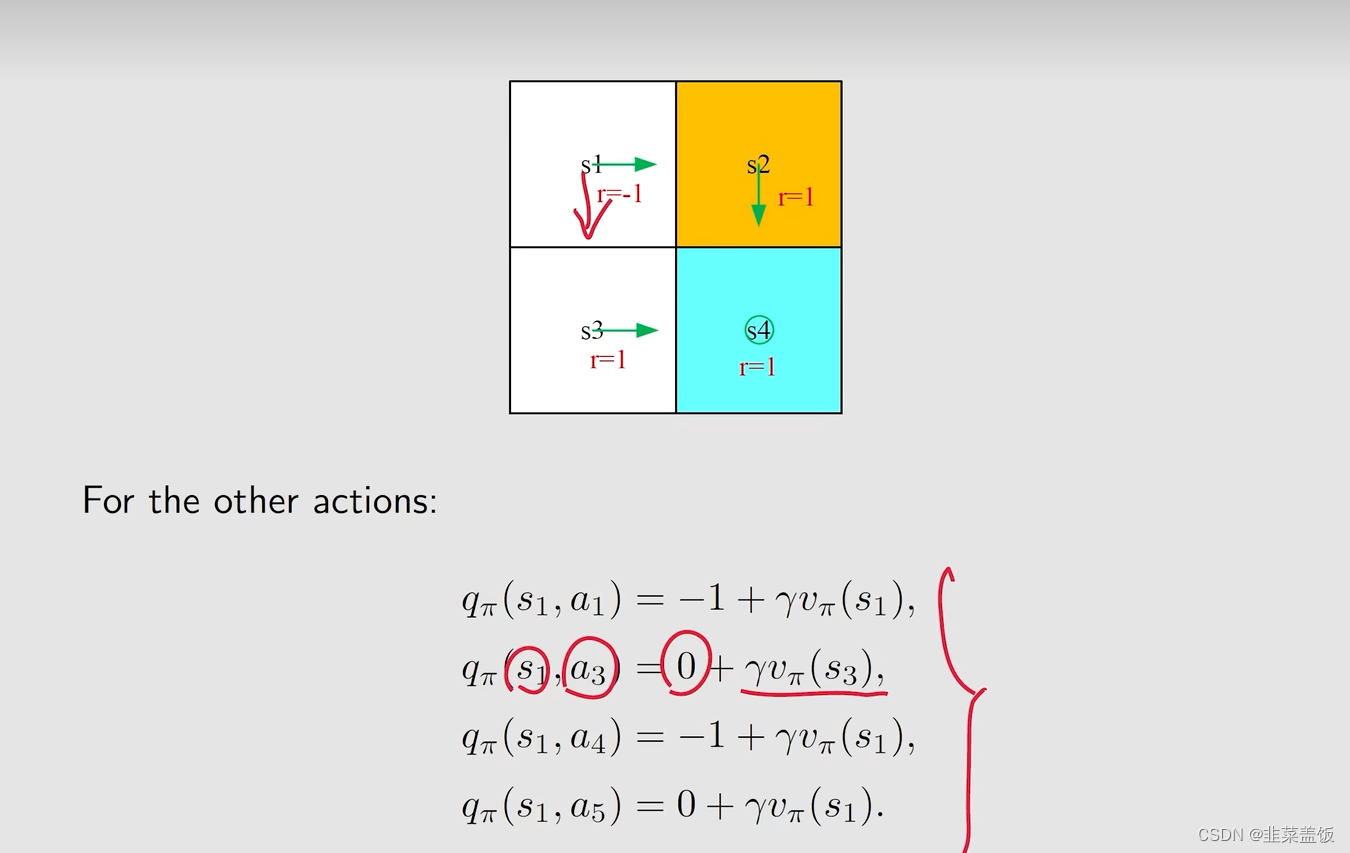
首先我们按照箭头的方向做出action,得到以下的Action value
q π ( s 1 , a 2 ) = − 1 + γ v π ( s 2 ) q_\pi(s_1,a_2) = -1 + γv_\pi(s_2) qπ(s1,a2)=−1+γvπ(s2)
虽然箭头是指向s2的(忽略红色箭头),但是我们依旧可以算其它方向的Action value,例如我们可以计算红色箭头的Action value
q π ( s 1 , a 3 ) = 0 + γ v π ( s 3 ) q_\pi(s_1,a_3) = 0 + γv_\pi(s_3) qπ(s1,a3)=0+γvπ(s3)(因为 s 1 s_1 s1到 s 3 s_3 s3都为空白格,所以奖励为0)
贝尔曼最优公式
在强化学习中,我们的目的就是找最优的策略,而贝尔曼方程的最优公式为我们提供了理论支撑
最优的定义:
我们有一个策略 π ∗ \pi^* π∗,在所有的状态s下以及所有其它策略 π \pi π下,存在 v π ∗ ( s ) v_{\pi^*}(s) vπ∗(s)大于所有的 v π ( s ) v_\pi(s) vπ(s)
我们称这个策略 π ∗ \pi^* π∗为最优策略
对于最优,我们有以下问题:
- 1、该策略是否存在?
- 2、该策略是否唯一?
- 3、该策略是确定性的还是非确定性的?
- 4、怎么去得到最优策略?
根据以上问题,我们需要研究贝尔曼最优公式,以下就是贝尔曼最优公式
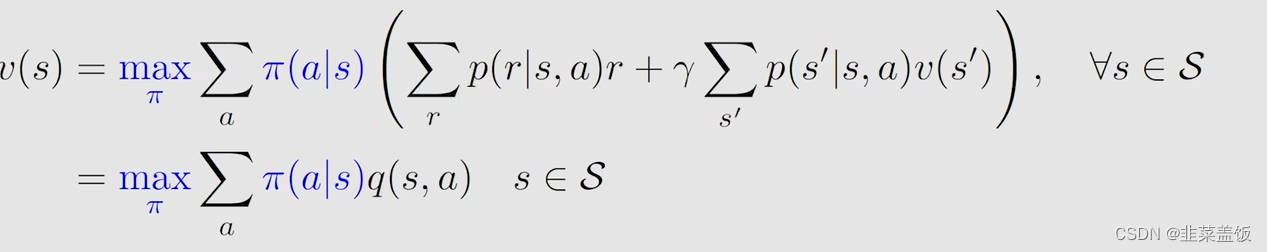
以下是贝尔曼方程最优公式的矩阵形式:
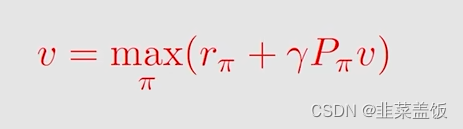
因为对于求解贝尔曼方程最优公式的推导有些复杂,视频中介绍了contraction mapping theorem来求解贝尔曼最优公式,我这里不详细给出,有兴趣的可以观看视频
我们只要知道,该方程存在一个唯一的解 v ∗ v^* v∗,且唯一存在,同时也可以利用迭代的方法求解出来
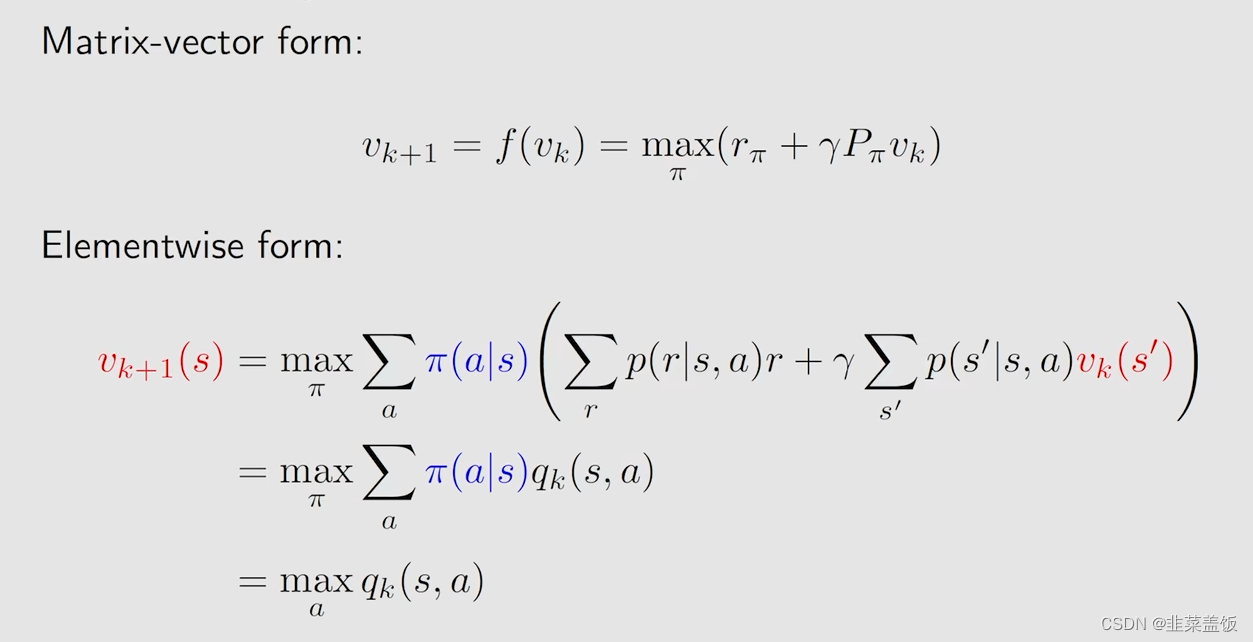
求解步骤如下:
1、对于任何状态s,当前的策略为 v k ( s ) v_k(s) vk(s)(初始化得到的)
2、对于任何action,我们计算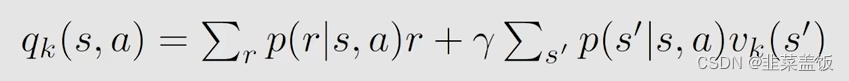
3、我们使用贪婪算法,选择最大的 q k ( s , a ) q_k(s,a) qk(s,a)
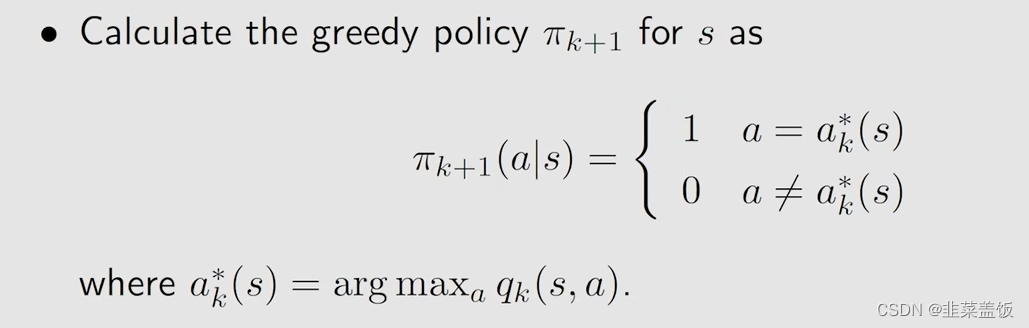
4、然后 v k + 1 ( s ) v_{k+1}(s) vk+1(s)就是最大的 q k ( s , a ) q_k(s,a) qk(s,a)
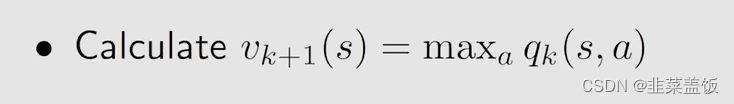
这个步骤迭代下去,就可以求出一个最优的策略 π \pi π