2925. 在树上执行操作以后得到的最大分数 - 力扣(LeetCode)
有一棵 n 个节点的无向树,节点编号为 0 到 n - 1 ,根节点编号为 0 。给你一个长度为 n - 1 的二维整数数组 edges 表示这棵树,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 有一条边。
同时给你一个长度为 n 下标从 0 开始的整数数组 values ,其中 values[i] 表示第 i 个节点的值。一开始你的分数为 0 ,每次操作中,你将执行:
- 选择节点
i。 - 将
values[i]加入你的分数。 - 将
values[i]变为0。
如果从根节点出发,到任意叶子节点经过的路径上的节点值之和都不等于 0 ,那么我们称这棵树是 健康的 。你可以对这棵树执行任意次操作,但要求执行完所有操作以后树是 健康的 ,请你返回你可以获得的 最大分数 。
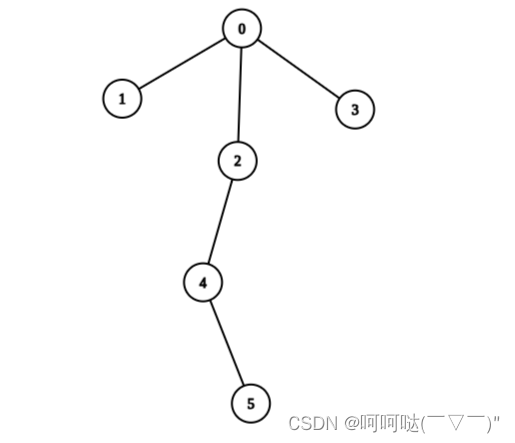
输入:edges = [[0,1],[0,2],[0,3],[2,4],[4,5]], values = [5,2,5,2,1,1] 输出:11 解释:我们可以选择节点 1 ,2 ,3 ,4 和 5 。根节点的值是非 0 的。所以从根出发到任意叶子节点路径上节点值之和都不为 0 。所以树是健康的。你的得分之和为 values[1] + values[2] + values[3] + values[4] + values[5] = 11 。11 是你对树执行任意次操作以后可以获得的最大得分之和。

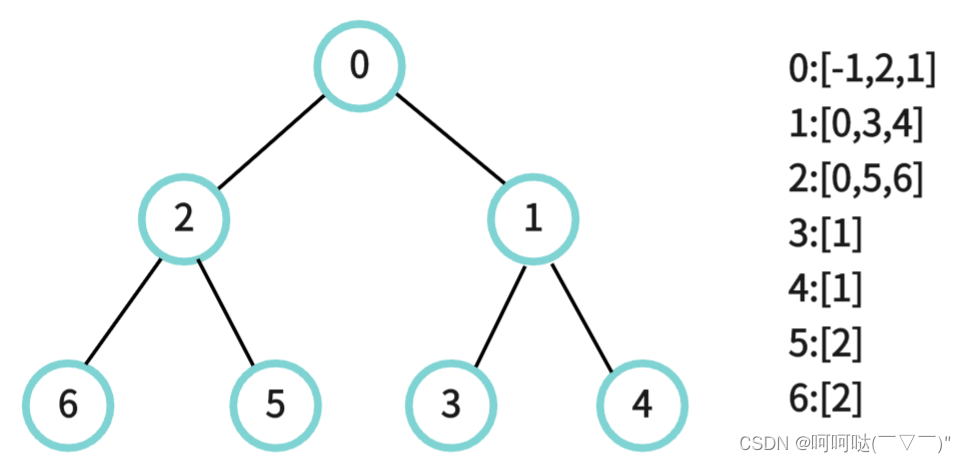
输入:edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], values = [20,10,9,7,4,3,5] 输出:40 解释:我们选择节点 0 ,2 ,3 和 4 。 - 从 0 到 4 的节点值之和为 10 。 - 从 0 到 3 的节点值之和为 10 。 - 从 0 到 5 的节点值之和为 3 。 - 从 0 到 6 的节点值之和为 5 。 所以树是健康的。你的得分之和为 values[0] + values[2] + values[3] + values[4] = 40 。 40 是你对树执行任意次操作以后可以获得的最大得分之和。
(方法一)参考灵神这篇文章:2925. 在树上执行操作以后得到的最大分数 - 力扣(LeetCode)
思路分析:题目中“如果从根节点出发,到任意叶子节点经过的路径上的节点值之和都不等于 0”。所在在执行操作时,每条从根节点到叶子节点的路径上,都存在一个节点不去操作(多条路径可能共用一个不操作的节点)
- 为了使得分数最大,不操作的节点之和应尽可能地小
定义一棵以 u 为根节点的健康子树:
- ① 要么不操作根节点 u ,此时这棵树是健康的,剩余的所有子节点都可以操作
- ② 要么操作根节点 u ,但是 u 的所有子树都需要保证自己是健康的
要得到最小和,取其两者情况的最小值

建图:
int n = values.size();
vector<vector<int>> g(n);
g[0].push_back(-1); // 避免误把根节点当作叶子
for(auto &e:edges) {int x = e[0], y = e[1];g[x].push_back(y);g[y].push_back(x);
}
class Solution {
public:long long maximumScoreAfterOperations(vector<vector<int>>& edges, vector<int>& values) {int n = values.size();vector<vector<int>> g(n);g[0].push_back(-1); // 避免误把根节点当作叶子for(auto &e:edges) {int x = e[0], y = e[1];g[x].push_back(y);g[y].push_back(x);}// dfs(x,fa) 计算以 x 为根的子树是健康时,失去的最小分数function<long long(int,int)> dfs = [&](int x,int fa)-> long long {if(g[x].size() == 1) { // x 是叶子return values[x];}long long loss = 0; // 第二种情况for(int y:g[x]) {if(y!=fa) {loss+=dfs(y,x);// 计算以 y 为根的子树是健康时,失去的最小分数}} return min((long long) values[x],loss); // 两种情况取最小值};long long sum = accumulate(values.begin(),values.end(),0LL);return sum - dfs(0,-1);}
};复杂度分析
- 时间复杂度:O(n),其中 n 为 values 的长度
- 空间复杂度:O(n)
(方法二)参考sad_path这篇文章2925. 在树上执行操作以后得到的最大分数 - 力扣(LeetCode)
class Solution {
public:class Node{public:Node(long x,int i) : val(x),index(i){}public:long val;int index;public:list<Node*> childArr;};long long maximumScoreAfterOperations(vector<vector<int>>& edges, vector<int>& values) {int n = values.size();// 建树,实际上是建图vector<Node *> nodes;for(int i=0;i<n;i++) {nodes.push_back(new Node(values[i],i));}for(auto &e:edges) {int x = e[0], y = e[1];nodes[x]->childArr.push_back(nodes[y]);nodes[y]->childArr.push_back(nodes[x]);}vector<bool> visited(n,false);visited[0] = true;long long sum = accumulate(values.begin(),values.end(),0LL);long long Min = dfs(nodes[0], visited);return sum - Min;}long long dfs(Node* root,vector<bool> visited) {int count = 0;long Min = 0;for (Node* child : root->childArr) {if (visited[child->index]) {count++;continue;}visited[child->index] = true;Min += dfs(child, visited);visited[child->index] = false;}// 此时该节点为叶节点,直接返回它的 valif (count == root->childArr.size()) {return root->val;}return min(root->val, Min);}
};