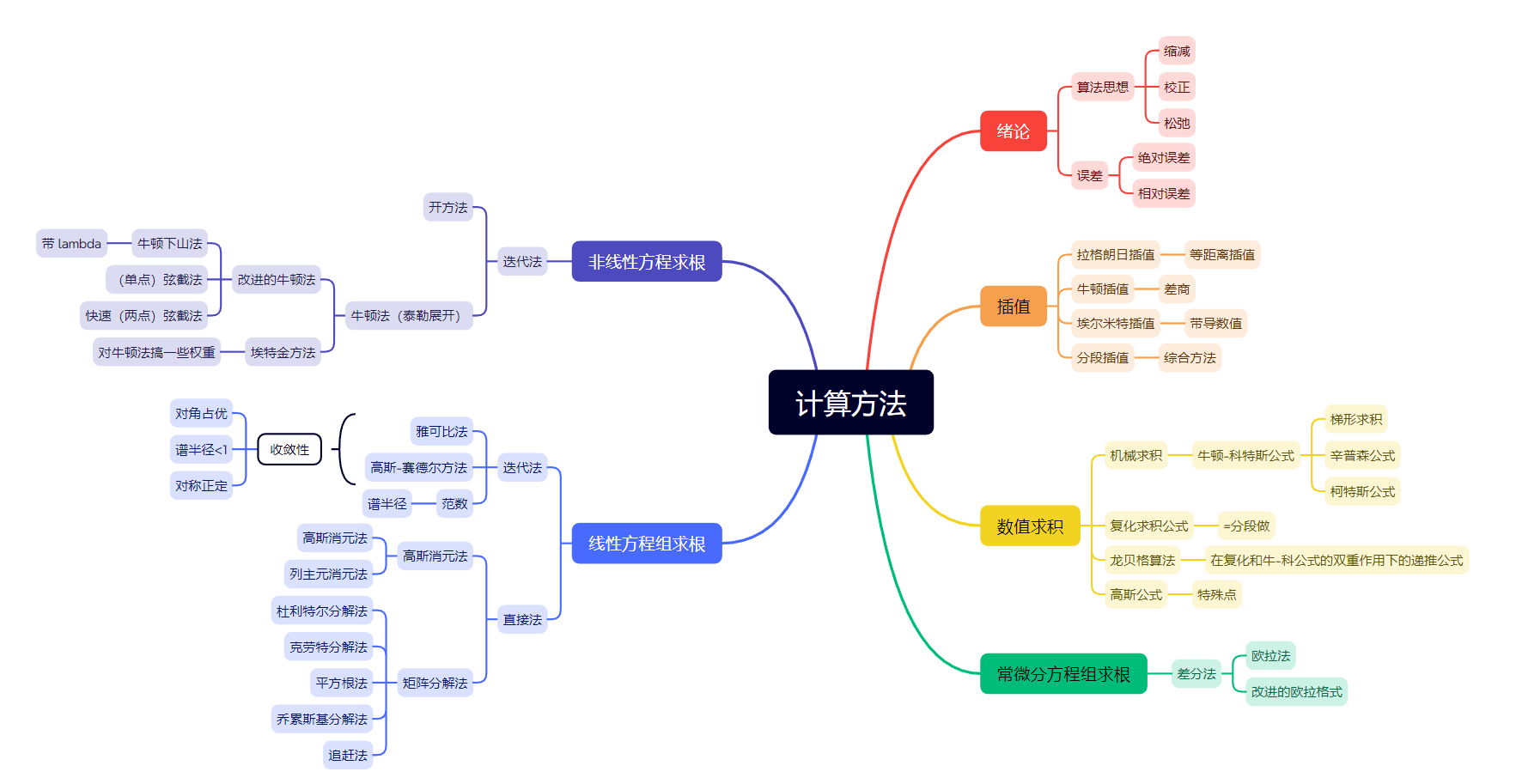
思维导图
绪论
算法的性质:
有穷性、确切性、有输入输出、可行性
算法的描述方法:
自然语言、伪代码、流程图、N-S流程图
算法设计思想:
- 化大为小的缩减技术:二分法
- 化难为易的校正技术:开方法
- 化粗为精的松弛技术:加权平均 超松弛 割圆术
误差来源:
- 模型/描述误差
- 观测误差
- 舍入如茶
- 初值误差
计算方法只研究后两类误差
误差的度量:
绝对误差 e ( x ∗ ) = x − x ∗ e(x^*)=x-x^* e(x∗)=x−x∗
绝对误差限 ∣ e ( x ∗ ) ∣ = ∣ x − x ∗ ∣ < ε |e(x^*)|=|x-x^*|<\varepsilon ∣e(x∗)∣=∣x−x∗∣<ε
相对误差 e r ( x ∗ ) = e ( x ∗ ) / x ≈ e ( x x ) / x ∗ e_r(x^*)=e(x^*)/x\approx e(x^x)/x^* er(x∗)=e(x∗)/x≈e(xx)/x∗
相对误差限
有效数字:
x ∗ = 1 0 m ∗ x 1 x 2 x 3 . . . . x p x^*=10^m *x_1x_2x_3....x_p x∗=10m∗x1x2x3....xp
∣ e ∣ < = 0.5 ∗ 1 0 m − n |e|<=0.5*10^{m-n} ∣e∣<=0.5∗10m−n,则具有n位有效数字
x ∗ x^* x∗准确到末位时,称有效数
选择算法原则:
- 避免相近的数相减
- 避免很小的数作分母
- 避免大数淹没小数
- 选用稳定性好的算法
插值
用多项式替代真实函数,该多项式存在且唯一(克莱姆法则证明)
拉格朗日插值
L n ( x ) = ∑ i = 0 n φ i ( x ) y i = ∑ i = 0 n ( ∏ j = 0 , j ! = i n x − x j x i − x j ) y i L_n(x)=\sum_{i=0}^n\varphi _i(x)y_i=\sum_{i=0}^n( {\textstyle \prod_{j=0,j!=i}^{n}\frac{x-x_j}{x_i-x_j} } )y_i Ln(x)=∑i=0nφi(x)yi=∑i=0n(∏j=0,j!=inxi−xjx−xj)yi
其中, φ ( x ) \varphi(x) φ(x)是插值基函数
本质上拉格朗日插值函数是加权和
特点:
- 插值点需要等距
- 新点进入需要重新计算基函数
- 高次插值的精度不一定高,可能产生龙格现象
牛顿插值
差商:
零阶差商: f ( x i ) = y i f(x_i)=y_i f(xi)=yi
一阶差商: f ( x i , x j ) = f ( x j ) − f ( x i ) x j − x i f(x_i,x_j)=\frac{f(x_j)-f(x_i)}{x_j-x_i} f(xi,xj)=xj−xif(xj)−f(xi)
二阶差商: f ( x i , x j , x k ) = f ( x j , x k ) − f ( x i , x j ) x k − x i f(x_i,x_j,x_k)=\frac{f(x_j,x_k)-f(x_i,x_j)}{x_k-x_i} f(xi,xj,xk)=xk−xif(xj,xk)−f(xi,xj)
可用表格法计算差商,对角线上的是系数
牛顿插值多项式:
p n ( x ) = f ( x 0 ) + f ( x 0 , x 1 ) ( x − x 0 ) + . . . + f ( x 0 , x 1 , . . . , x n ) ( x − x 0 ) ( x − x 1 ) . . . ( x − x n − 1 ) p_n(x)=f(x_0)+f(x_0,x_1)(x-x_0)+...+f(x_0,x_1,...,x_n)(x-x_0)(x-x_1)...(x-x_{n-1}) pn(x)=f(x0)+f(x0,x1)(x−x0)+...+f(x0,x1,...,xn)(x−x0)(x−x1)...(x−xn−1)
特点:
- 和拉格朗日插值结果一致
- 不需要重新计算基函数
- 不需要插值点等距
埃米尔特Hermite插值(切触插值)
两点三次插值:
p 3 ( x ) = y 0 φ 0 ( x ) + y 1 φ 1 ( x ) + y 0 ′ ψ 0 ( x ) + y 1 ′ ψ 1 ( x ) p_3(x)=y_0\varphi_0(x)+y_1\varphi_1(x)+y_0'\psi _0(x)+y_1'\psi _1(x) p3(x)=y0φ0(x)+y1φ1(x)+y0′ψ0(x)+y1′ψ1(x)
其中 φ 0 ( x ) = ( 1 + 2 x − x 0 x 1 − x 0 ) ( x − x 1 x 0 − x 1 ) 2 \varphi_0(x)=(1+2\frac{x-x_0}{x_1-x_0} )(\frac{x-x_1}{x_0-x_1} )^2 φ0(x)=(1+2x1−x0x−x0)(x0−x1x−x1)2
φ 1 ( x ) = ( 1 + 2 x − x 1 x 0 − x 1 ) ( x − x 0 x 1 − x 0 ) 2 \varphi_1(x)=(1+2\frac{x-x_1}{x_0-x_1} )(\frac{x-x_0}{x_1-x_0} )^2 φ1(x)=(1+2x0−x1x−x1)(x1−x0x−x0)2
ψ 0 ( x ) = ( x − x 0 ) ( x − x 0 x 0 − x 1 ) 2 \psi_0(x)=(x-x_0)(\frac{x-x_0}{x_0-x_1} )^2 ψ0(x)=(x−x0)(x0−x1x−x0)2
ψ 1 ( x ) = ( x − x 1 ) ( x − x 0 x 1 − x 0 ) 2 \psi_1(x)=(x-x_1)(\frac{x-x_0}{x_1-x_0} )^2 ψ1(x)=(x−x1)(x1−x0x−x0)2
特点:
- 具有导数值
分段插值
大一统的方法,在段内,想用哪种插就用哪种插!
数值积分
正统方法是牛顿-莱布尼茨公式,但是我们又算不出来,不想算,咋办呢
代数精度
一个公式,对于不超过m次的任意多项式都准确,但对m+1次有不准确的,那么具有m阶代数精度。
简化一下,用1,x, x 2 x^2 x2往里带就行
机械求积
∫ a b f ( x ) d x = ( b − a ) ∑ i = 0 n λ i f ( x i ) \int_{a}^{b} f(x)dx=(b-a)\sum_{i=0}^n\lambda_if(x_i) ∫abf(x)dx=(b−a)∑i=0nλif(xi) 加权和
梯形求积公式
∫ a b f ( x ) d x = ( b − a ) / 2 ( f ( a ) + f ( b ) ) \int_{a}^{b} f(x)dx=(b-a)/2 (f(a)+f(b)) ∫abf(x)dx=(b−a)/2(f(a)+f(b))
牛顿-科特斯公式
将求积区间[a,b]划分为n等分,用等分点构造拉格朗日插值,用L(x)代替f(x)
| n | 求积系数1 | 求积系数2 | 求积系数3 | 求积系数4 | 求积系数5 |
|---|---|---|---|---|---|
| 1 | 1/2 | 1/2 | |||
| 2 | 1/6 | 4/6 | 1/6 | ||
| 3 | 1/8 | 3/8 | 3/8 | 1/8 | |
| 4 | 7/90 | 16/45 | 2/15 | 16/45 | 7/90 |
其中n=1为梯形求积公式,n=2为辛普森公式,n=4为科特四公式
奇数的代数精度和前一个偶数一样,所以正常人没人用奇数的
代数精度分别为1,3,3,5
复化求积公式
跟分段插值一样
复化梯形: I = b − a 2 n ( f ( a ) + 2 ∑ i = 1 n − 1 f ( x i ) + f ( b ) ) I=\frac{b-a}{2n}(f(a)+2 {\textstyle \sum_{i=1}^{n-1}}f(x_i)+f(b)) I=2nb−a(f(a)+2∑i=1n−1f(xi)+f(b))
复化辛普森公式: I = b − a 6 n ( f ( a ) + 4 ∑ i = 0 n − 1 f ( x i + 1 / 2 ) + 2 ∑ i = 1 n − 1 f ( x i ) + f ( b ) ) I=\frac{b-a}{6n}(f(a)+4 {\textstyle \sum_{i=0}^{n-1}}f(x_{i+1/2})+2{\textstyle \sum_{i=1}^{n-1}f(x_i)}+f(b)) I=6nb−a(f(a)+4∑i=0n−1f(xi+1/2)+2∑i=1n−1f(xi)+f(b))
复化柯特斯公式: I = b − a 90 n ( f ( a ) + 32 ∑ i = 0 n − 1 f ( x i + 1 / 4 ) + 12 ∑ i = 0 n − 1 f ( x i + 1 / 2 ) + 32 ∑ i = 0 n − 1 f ( x i + 3 / 4 ) + 14 ∑ i = 1 n − 1 f ( x i ) + 7 f ( b ) ) I=\frac{b-a}{90n}(f(a)+32 {\textstyle \sum_{i=0}^{n-1}}f(x_{i+1/4})+12 {\textstyle \sum_{i=0}^{n-1}}f(x_{i+1/2})+32 {\textstyle \sum_{i=0}^{n-1}}f(x_{i+3/4})+14 {\textstyle \sum_{i=1}^{n-1}}f(x_{i})+7f(b)) I=90nb−a(f(a)+32∑i=0n−1f(xi+1/4)+12∑i=0n−1f(xi+1/2)+32∑i=0n−1f(xi+3/4)+14∑i=1n−1f(xi)+7f(b))
龙贝格算法(kao)?
T 1 = ( b − a ) / 2 ( f ( a ) + f ( b ) ) T_1=(b-a)/2 (f(a)+f(b)) T1=(b−a)/2(f(a)+f(b)) 一个梯形
T 2 n = 1 / 2 T 1 + 2 / h ∑ i = 0 n − 1 f ( x i + 1 / 2 ) T_{2n}=1/2 \ T_1+2/h\ {\textstyle \sum_{i=0}^{n-1}}f(x_{i+1/2}) T2n=1/2 T1+2/h ∑i=0n−1f(xi+1/2)
S n = 4 / 3 T 2 n − 1 / 3 T n S_n=4/3\ T_{2n}-1/3 \ T_n Sn=4/3 T2n−1/3 Tn
C n = 16 / 15 S 2 n − 1 / 15 S n C_n=16/15\ S_{2n}-1/15 \ S_n Cn=16/15 S2n−1/15 Sn
R n = 64 / 63 C 2 n − 1 / 63 C n R_n=64/63\ C_{2n}-1/63 \ C_n Rn=64/63 C2n−1/63 Cn
高斯公式
求积节点不是等分,而是一些特殊点
∫ a b f ( x ) d x = b − a 2 ∫ − 1 1 g ( t ) d t \int_{a}^{b}f(x)dx=\frac{b-a}{2}\int_{-1}^{1}g(t)dt ∫abf(x)dx=2b−a∫−11g(t)dt,见资料积分区间转换
一点: ∫ − 1 1 f ( x ) d x ≈ 2 f ( 0 ) \int_{-1}^{1}f(x)dx\approx 2f(0) ∫−11f(x)dx≈2f(0)
两点: ∫ − 1 1 f ( x ) d x ≈ f ( − 1 3 ) + f ( 1 3 ) \int_{-1}^{1}f(x)dx\approx f(-\frac{1}{\sqrt{3} } )+f(\frac{1}{\sqrt{3} }) ∫−11f(x)dx≈f(−31)+f(31)
三点: ∫ − 1 1 f ( x ) d x ≈ 5 9 f ( − 3 5 ) + 8 9 f ( 0 ) + 5 9 f ( 3 5 ) \int_{-1}^{1}f(x)dx\approx \frac{5}{9 }f(-\sqrt\frac{3}{{5} } )+\frac{8}{9} f(0)+\frac{5}{9} f(\sqrt{\frac{3}{5} } ) ∫−11f(x)dx≈95f(−53)+98f(0)+95f(53)
一般积分区间的高斯公式
方程求根的迭代法
x k + 1 = φ ( x k ) x_{k+1}=\varphi(x_k) xk+1=φ(xk)
导数的绝对值<=1时,收敛
开方算法
x 0 > 0 x_0>0 x0>0
x k + 1 = 1 2 ( x k + a x k ) x_{k+1}=\frac{1}{2}(x_k+\frac{a}{x_k}) xk+1=21(xk+xka)
牛顿法(重点)
泰勒展开前两项,得到 x k + 1 = x k − f ( x k ) f ′ ( x k ) x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)} xk+1=xk−f′(xk)f(xk)
使用条件:
- 介值定理
- f’(x)!=0
- f’'(x)存在且不变号
- x0选点必须使得f’'(x)f(x0)>0
如此才能收敛
收敛速度
e k + 1 e k p \frac{e_{k+1}}{e_k^p} ekpek+1->C 则迭代过程是p阶收敛的
牛顿法为平方收敛
牛顿下山法
要求|函数值|单调下降
得到 x k + 1 = x k − λ f ( x k ) f ′ ( x k ) x_{k+1}=x_k-\lambda \frac{f(x_k)}{f'(x_k)} xk+1=xk−λf′(xk)f(xk)
0 < λ < 1 0<\lambda<1 0<λ<1,称下山因子,逐步探索下山因子,从1开始,如果有一步始终找不到,则重选初值
(单点)弦截法
令 f ′ ( x k ) ≈ f ( x k ) − f ( x 0 ) x k − x 0 f'(x_k)\approx \frac{f(x_k)-f(x_0)}{x_k-x_0} f′(xk)≈xk−x0f(xk)−f(x0),用割线代替切线
快速/两点 弦截法
需要两个初值x0和x1
埃特金迭代公式
x k + 1 ˉ = φ ( x k ) \bar{x_{k+1}}=\varphi (x_k) xk+1ˉ=φ(xk) 牛顿一次
x k + 1 ~ = φ ( x k + 1 ˉ ) \tilde{x_{k+1}}=\varphi (\bar{x_{k+1}} ) xk+1~=φ(xk+1ˉ) 再牛顿一次
x k + 1 = x k + 1 ~ − ( x k + 1 ~ − x k + 1 ˉ ) 2 x k + 1 ~ − 2 x k + 1 ˉ + x k x_{k+1}=\tilde{x_{k+1}}-\frac{(\tilde{x_{k+1}}-\bar{x_{k+1}})^2}{\tilde{x_{k+1}}-2\bar{x_{k+1}}+x_k} xk+1=xk+1~−xk+1~−2xk+1ˉ+xk(xk+1~−xk+1ˉ)2 奇怪的加权!
线性方程组的迭代法
Jacobi
x k + 1 = − D − 1 ( L + U ) x + D − 1 b x_{k+1}=-D^{-1}(L+U)x+D^{-1}b xk+1=−D−1(L+U)x+D−1b
移过去,用xk算
Gauss-Seidel
x k + 1 = − ( D + L ) − 1 U x + ( D + L ) − 1 b x_{k+1}=-(D+L)^{-1}Ux+(D+L)^{-1}b xk+1=−(D+L)−1Ux+(D+L)−1b
移过去,用 x k + 1 x_{k+1} xk+1算
收敛判断
Jacobi迭代法和Gauss-Seidel迭代法的收敛性
范数
向量的1范数=x绝对值之和
2范数=欧氏距离
无穷范数=绝对值的最大值
矩阵的1范数是列范数,对每列的绝对值求和,找个最大的列
2范数是谱范数 ∣ ∣ A ∣ ∣ 2 = λ m a x ( A T A ) ||A||_2=\sqrt{\lambda_{max}(A^TA)} ∣∣A∣∣2=λmax(ATA)
无穷范数是行范数,也许因为它是横着的吧(?
谱半径:A绝对值最大的特征值
对任意矩阵范数,谱半径都<=范数,所以范数要是<1,迭代法是不是就必然收敛了呢~
线性方程组的直接法
高斯消元法
化成上下三角形,这也要说?
列主元消元法
换行再消元
矩阵分解法
可以分解为LU 一个下三角和一个上三角的乘积,其中一个是单位的
- Doolittle分解法
先横着算u,再竖着算l - crout分解法
先竖着算l,再横着算u
有公式但是记不住,现推吧
- 平方根法分解 A= L L T LL^T LLT 有公式
- Cholesky分解 正定矩阵分解为 A = L D L T A=LDL^T A=LDLT代价<平方根
- 追赶法 三对角矩阵适用 消元+回代
常微分方程的差分法
欧拉格式
向前的 y ( x n + 1 ) ≈ y ( x n ) + h f ( x n , y ( x n ) ) y(x_{n+1})\approx y(x_n)+hf(x_n,y(x_n)) y(xn+1)≈y(xn)+hf(xn,y(xn))
向后的(隐式) y ( x n + 1 ) ≈ y ( x n ) + h f ( x n + 1 , y ( x n + 1 ) ) y(x_{n+1})\approx y(x_n)+hf(x_{n+1},y(x_{n+1})) y(xn+1)≈y(xn)+hf(xn+1,y(xn+1))
两步 y ( x n + 1 ) ≈ y n − 1 + 2 h f ( x n , y ( x n ) ) y(x_{n+1})\approx y_{n-1}+2hf(x_{n},y(x_{n})) y(xn+1)≈yn−1+2hf(xn,y(xn)) 无法直接启动
梯形格式 y ( x n + 1 ) ≈ h 2 ( f ( x n , y ( x n ) ) + f ( x n + 1 , y ( x n + 1 ) ) y(x_{n+1})\approx \frac{h}{2}(f(x_{n},y(x_{n}))+f(x_{n+1},y(x_{n+1})) y(xn+1)≈2h(f(xn,y(xn))+f(xn+1,y(xn+1))这也是隐式的,也没法用(二阶)
改进的欧拉格式
二阶代数精度
先预报,再校正
预报值 y ( x n + 1 ) ˉ = y ( x n ) + h f ( x n , y ( x n ) ) \bar{y(x_{n+1})}= y(x_n)+hf(x_n,y(x_n)) y(xn+1)ˉ=y(xn)+hf(xn,y(xn))
校正值 y ( x n + 1 ) ≈ y ( x n ) + h 2 ( f ( x n , y ( x n ) ) + f ( x n + 1 y ( x n + 1 ) ˉ ) y(x_{n+1})\approx y(x_n)+\frac{h}{2}(f(x_{n},y(x_{n}))+f(x_{n+1}\bar{y(x_{n+1})}) y(xn+1)≈y(xn)+2h(f(xn,y(xn))+f(xn+1y(xn+1)ˉ)
可以简化表示为: