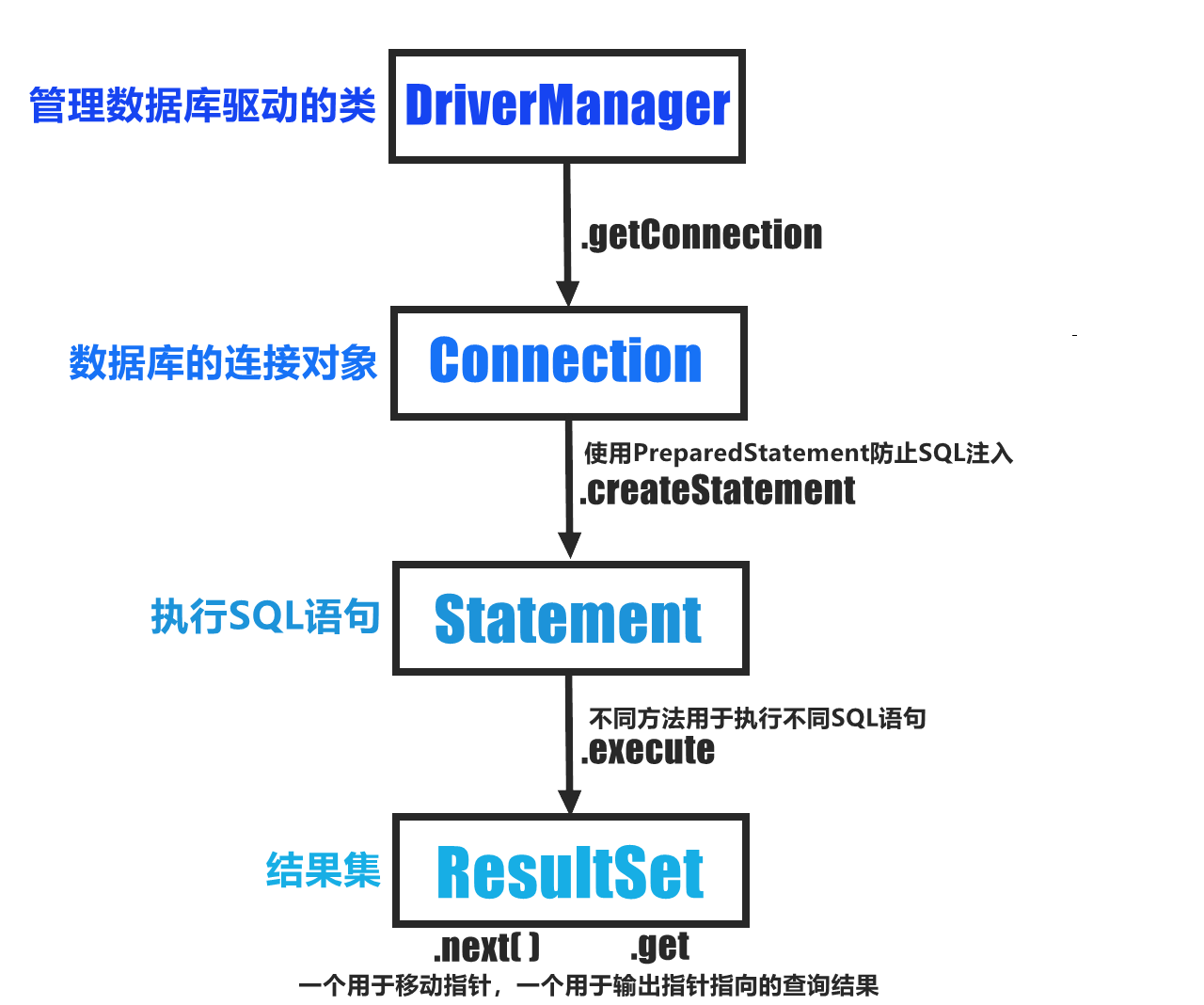
上链接：P4017 最大食物链计数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
https://www.luogu.com.cn/problem/P4017
上题干：
题目背景
你知道食物链吗？Delia 生物考试的时候，数食物链条数的题目全都错了，因为她总是重复数了几条或漏掉了几条。于是她来就来求助你，然而你也不会啊！写一个程序来帮帮她吧。
题目描述
给你一个食物网，你要求出这个食物网中最大食物链的数量。
（这里的“最大食物链”，指的是生物学意义上的食物链，即最左端是不会捕食其他生物的生产者，最右端是不会被其他生物捕食的消费者。）
Delia 非常急，所以你只有 11 秒的时间。
由于这个结果可能过大，你只需要输出总数模上 8011200280112002 的结果。
输入格式
第一行，两个正整数 n、m，表示生物种类 n 和吃与被吃的关系数 m。
接下来 m 行，每行两个正整数，表示被吃的生物A和吃A的生物B。
输出格式
一行一个整数，为最大食物链数量模上 80112002 的结果。
输入输出样例
输入 #1复制
5 7 1 2 1 3 2 3 3 5 2 5 4 5 3 4输出 #1复制
5说明/提示
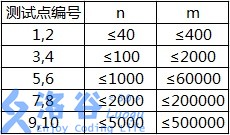
各测试点满足以下约定：
【补充说明】
数据中不会出现环，满足生物学的要求。
数据大小:M=5e5+7，N=5e3+7
取模：mod=80112002
一个vector 用来储存点的关系，
一个数组f来储存答案。
一个数组outd表示入度，
一个数组ind表示出度。
一个队列q每次用来增加新的入度为0的点，和删除已经用过的入度为0的点。
开始分析：
我们要求所有的完整食物链的个数，也就是求所有起点是生产者，终点是最高级的消费者。
我们可以得到这样的图：
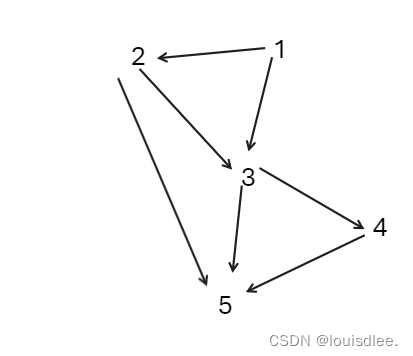
假设数组f【i】表示以生产者为起点，到i号生物的路径数量。
由此我们可以得到递推关系。
f【5】= f【2】+f【3】+f【4】
f【2】=f【1】
f【3】=f【2】+f【1】
f【4】=f【3】
f【1】=1；
这就是这样例的结果。f【5】=1+2+2=5
先将所有入度为0的数字的f【】初始化为1，其他的初始化为0；
1对其他能吃它的贡献为f【1】，现在我们将1删除，然后将1的捕食关系删除，也就是能吃1的入度-1，然后给它们加上f【1】，也就是f【2】=f【1】，f【3】=f【1】
现在场上剩下的图像就是：
继续找入度为0的点，现在是2，那么删去2，给能吃2的加上2的贡献，
f【3】=f【1】+f【2】
f【5】=f【2】
然后删除后的图像就是这样：
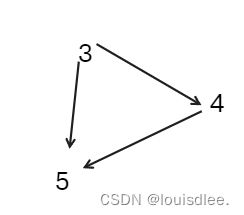
继续找图中入度为0的点：3
删除3的痕迹，给能吃3的加上3的贡献
f【5】=f【2】+f【3】
f【4】=f【3】
最后删除4，以及4 的痕迹，给能吃4的加上4的贡献
f【5】=f【2】+f【3】+f【4】=5
此时剩下的一定是最高消费者，那么其代表的数值就一定是答案。
上代码：
const int mod = 80112002;
const int M = 5e5+7;
const int N = 5e3 + 7;
queue<int > q;
int outd[N];
int ind[N];
int f[N];
int ans;
vector<int > p[N];
int main()
{int n, m;cin >> n >> m;for (int i = 0; i < m; i++){int a, b;cin >> a >> b;p[b].push_back(a);outd[b]++;ind[a]++;}for (int i = 1; i <= n; i++){if (ind[i] == 0) {q.push(i);f[i] = 1;}}while (!q.empty()) {int x = q.front();q.pop();for (int i = 0; i < p[x].size(); i++){f[p[x][i]] += f[x];f[p[x][i]] %= mod;ind[p[x][i]]--;if (ind[p[x][i]] == 0)q.push(p[x][i]);}}for (int i = 1; i <= n; i++){if (outd[i] == 0)ans = (ans+f[i])%mod;}cout << ans;
}
