前言

本课程来自深度之眼，部分截图来自课程视频。
文章标题：Semi-Supervised Classification with Graph Convolutional Networks
图卷积神经网络的半监督分类（GCN）
作者：Thomas N.Kipf，Max Welling
单位：University of Amsterdam
发表会议及时间：ICLR 2017
公式输入请参考：在线Latex公式
之前写的有点问题，重新编辑发现CSDN对文章长度做了限制，只能切开变成上下两篇了

细节四：卷积核介绍

图卷积核初代目

这节通过几篇图卷积相关的论文来讲解图卷积核的演变过程。
Spectral Networks and Deep Locally Connected Networks on Graphs
早期的图卷积的论文，其思想是利用公式14（其中f是图的输入，h是卷积核，对这两货分别进行频域的变化后，做elementwise点乘，然后再逆变换回图信号。）
$$(f\ast h{)}_G=U((U^{T}h)\odot (U^{T}f))\text{\hspace{1em}(14)}$$
写出计算图某个节点表征的公式：
$$y_{output}=\sigma (U{g}_{\theta }(\Lambda )U^{T}x)\text{\hspace{1em}(18)}$$
其中$g_{\theta }(\Lambda )$就是公式15中的对角线矩阵，这里写成：
$$g_{\theta }(\Lambda )=\left(\begin{array}{ccc}{\theta }_1& & \\ & \ddots & \\ & & {\theta }_n\end{array}\right)\text{\hspace{1em}(19)}$$
由于公式18要计算特征向量$U$，要对拉普拉斯矩阵进行分解，另外加上矩阵的乘法，计算复杂度比较高，公式18中x是节点的特征，整个公式中$\theta$是要学习的参数，共有n个，整个过程针对所有节点没有利用邻居信息，没有localization。
Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering
这篇论文中用另外一种形式来表示公式18中的$g_{\theta }(\Lambda )$
$$g_{\theta }(\Lambda )=\left(\begin{array}{ccc}{\sum }_{j=0}^{K-1}{\alpha }_j{\lambda }_1^j& & \\ & \ddots & \\ & & {\sum }_{j=0}^{K-1}{\alpha }_j{\lambda }_n^j\end{array}\right)=\sum _{j=0}^{K-1}{\alpha }_j{\Lambda }^j\text{\hspace{1em}(20)}$$
将公式20的卷积核代入18，只看$U{g}_{\theta }(\Lambda )U^T$这个部分：
$$U{g}_{\theta }(\Lambda )U^T=U\sum _{j=0}^{K-1}{\alpha }_j{\Lambda }^j(\Lambda )U^T=\sum _{j=0}^{K-1}{\alpha }_{j}U{\Lambda }^j{U}^T=\sum _{j=0}^{K-1}{\alpha }_j{L}^j\text{\hspace{1em}(21)}$$
可以看到公式21的最后形态直接是拉普拉斯矩阵，没有特征向量U，也就意味不需要矩阵的特征分解。下面看下公式21的简单证明过程：

---

因为$U^{T}U=E$，
$$L^2=LL=U\Lambda U^{T}U\Lambda U^T=U{\Lambda }^2{U}^T$$
同理：
$$L^3=U{\Lambda }^3{U}^T$$
$$⋮$$
$$L^n=U{\Lambda }^n{U}^T$$
因此公式21中的
$$U{\Lambda }^j{U}^T=L^j$$

---

因此公式18变成了：
$$y_{output}=\sigma (\sum _{j=0}^{K-1}{\alpha }_j{L}^{j}x)$$
从推导过程我们可以知道，这个卷积核不用特征分解，因此计算复杂度低；参数量从n变成了K个，K<n；而且比较重要的一点，就是$L^j$，相当于邻居矩阵：$A^j$，当j=1时，表示节点的直接邻居信息，j=2时，表示1跳邻居，当j=n时，表示的是n-1跳邻居，不再针对所有节点，而是只对j-1跳邻居进行计算，实现了localization。

图卷积核二代目

还是同样的文章里面
Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering
介绍了契比雪夫Chebyshev多项式卷积核，也是本文GCN用的卷积核。
同样的，是将中的$g_{\theta }(\Lambda )$换成另外一种形式，即替换为契比雪夫多项式：
$$g_{\theta }(\Lambda )=\sum _{j=0}^{K-1}{\beta }_k{T}_k(\tilde{\Lambda })$$
其中${\beta }_k$是我们要学习的参数，后面则是契比雪夫多项式（特征值矩阵做为输入）
$$T_k(x)=\cos (k\cdot \arccos (x))\text{\hspace{1em}(22)}$$
公式22中$arccos(x)$的定义域为[-1,1]，而拉普拉斯的特征值取值范围是大于0的实数，因此要将拉普拉斯的特征值映射到[-1,1]上：
先将$\frac{\Lambda }{{\lambda }_{max}}$，这样特征值取值范围就变成了[0,1]，然后使得：
$$\tilde{\Lambda }=2\frac{\Lambda }{{\lambda }_{max}}-I$$
特征值取值范围就变成了$2\times [0,1]-1$，变成了[-1,1]。
这里是对特征向量做操作，我们是要避免矩阵分解的，因此，如果我们直接对拉普拉斯矩阵做上面的缩放操作，也会使得缩放后的矩阵的特征向量的取值范围变成了[-1,1]：
$$\tilde{L}=2\frac{L}{{\lambda }_{max}}-I$$

---

说明：
这里虽然还是涉及到了${\lambda }_{max}$，但是在线代里面求最大那个特征向量${\lambda }_{max}$可以不涉及特征分解。

---

契比雪夫多项式具有如下性质：
$$T_k(\tilde{L})=2\tilde{L}{T}_{k-1}(\tilde{L})-T_{k-2}(\tilde{L})$$
$$T_0(\tilde{L})=I,T_1(\tilde{L})=\tilde{L}\text{\hspace{1em}(23)}$$
GCN其实就是用了公式23（契比雪夫多项式）的第0项和第1项
接下来继续看：
$$\begin{array}{rl}{y}_{output}& =\sigma (U{g}_{\theta }(\Lambda )U^{T}x)\\ & =\sigma (U\sum _{j=0}^{K-1}{\beta }_k{T}_k(\tilde{\Lambda })U^{T}x)\end{array}$$
由于契比雪夫多项式是用特征值对角矩阵进行的输入，因此可以把两边的矩阵放到里面一起操作：
$$y_{output}=\sigma (\sum _{j=0}^{K-1}{\beta }_k{T}_k(U\tilde{\Lambda }{U}^T)x)$$
$U\tilde{\Lambda }{U}^T$这项在上面证明过，就是等于$\tilde{L}$的
因此，最后的推导结果为：
$$y_{output}=\sigma (\sum _{j=0}^{K-1}{\beta }_k{T}_k(\tilde{L})x)$$

契比雪夫多项式例子

假设有如下无向图（这个图上面也有）：

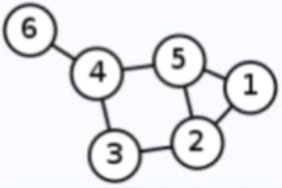
当k=0时，根据公式23：
$$\sum _{j=0}^{K-1}{\beta }_k{T}_k(\tilde{L})={\beta }_0{T}_0(\tilde{L})={\beta }_{0}I={\beta }_0$$
那么这个时候的卷积核为：
$$\left(\begin{array}{cccccc}{\beta }_0& 0& 0& 0& 0& 0\\ 0& {\beta }_0& 0& 0& 0& 0\\ 0& 0& 0{\beta }_0& 0& 0& 0\\ 0& 0& 0& {\beta }_0& 0& 0\\ 0& 0& 0& 0& {\beta }_0& 0\\ 0& 0& 0& 0& 0& {\beta }_0\end{array}\right)$$
当k=1时，根据公式23：
$$\sum _{j=0}^{K-1}{\beta }_k{T}_k(\tilde{L})={\beta }_0{T}_0(\tilde{L})+{\beta }_1{T}_1(\tilde{L})={\beta }_0+{\beta }_1\tilde{L}$$
$$L=I-D^{-0.5}A{D}^{-0.5}$$
度矩阵：
$$D=\left(\begin{array}{cccccc}2& 0& 0& 0& 0& 0\\ 0& 3& 0& 0& 0& 0\\ 0& 0& 2& 0& 0& 0\\ 0& 0& 0& 3& 0& 0\\ 0& 0& 0& 0& 3& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right)$$
邻接矩阵：
$$A=\left(\begin{array}{cccccc}0& 1& 0& 0& 1& 0\\ 1& 0& 1& 0& 1& 0\\ 0& 1& 0& 1& 0& 0\\ 0& 0& 1& 0& 1& 1\\ 1& 1& 0& 1& 0& 0\\ 0& 0& 0& 1& 0& 0\end{array}\right)$$

$$D^{-0.5}A{D}^{-0.5}=\left(\begin{array}{cccccc}0& 1/2& 0& 0& 1/2& 0\\ 1/3& 0& 1/3& 0& 1/3& 0\\ 0& 1/2& 0& 1/2& 0& 0\\ 0& 0& 1/3& 0& 1/3& 1/3\\ 1/3& 1/3& 0& 1/3& 0& 0\\ 0& 0& 0& 1& 0& 0\end{array}\right)$$
$$L=I-D^{-0.5}A{D}^{-0.5}=\left(\begin{array}{cccccc}1& -1/2& 0& 0& -1/2& 0\\ -1/3& 1& -1/3& 0& -1/3& 0\\ 0& -1/2& 1& -1/2& 0& 0\\ 0& 0& -1/3& 1& -1/3& -1/3\\ -1/3& -1/3& 0& -1/3& 1& 0\\ 0& 0& 0& -1& 0& 1\end{array}\right)$$
然后按照公式将$L$变成$\tilde{L}$
$$\tilde{L}=2\frac{L}{{\lambda }_{max}}-I$$
L的最大特征值${\lambda }_{max}$约为：1.87667（https://zs.symbolab.com/）
可以看到当k=1的时候，实际上就是加入了图邻接一跳的邻居信息。

小结

1.切比雪夫多项式的递归定义：
$$\{\begin{array}{ll}& T_0(x)=1\\ & T_1(x)=x\\ & T_{n+1}(x)=2x{T}_n(x)-T_{n-1}(x)\end{array}$$
2.切比雪夫卷积核：
$$\{\begin{array}{ll}& g_{{\theta }^{\prime }}(\Lambda )\approx {\sum }_{k=0}^{K-1}{\theta }_k^{\prime }{T}_k(\tilde{\Lambda })\\ & \tilde{\Lambda }=\frac{2}{{\lambda }_{max}}\Lambda -I_N\end{array}$$
3.切比雪夫图卷积：
$$\{\begin{array}{ll}& g_{{\theta }^{\prime }}\star x\approx {\sum }_{k=0}^{K-1}{\theta }_k^{\prime }{T}_k(\tilde{L})x\\ & \tilde{L}=\frac{2}{{\lambda }_{max}}L-I_N\end{array}$$

GCN公式推导

铺垫了这么多，终于到了正题，原文对应第二节，前面几个公式都用的切比雪夫的，不用多说，从公式6看：
$$g_{{\theta }^{\prime }}\star x\approx \sum _{k=0}^{K-1}{\theta }_k^{\prime }{T}_k(\tilde{L})x$$
如果只考虑k=0和k=1：
$$g_{{\theta }^{\prime }}\star x\approx {\theta }_0^{\prime }x+{\theta }_1^{\prime }\tilde{L}x={\theta }_0^{\prime }x+{\theta }_1^{\prime }(\frac{2}{{\lambda }_{max}}L-I_N)x$$
论文中提到GCN的${\lambda }_{max}\approx 2$，代入上面可以得（为什么是2看这里，老师提供了链接：https://zhuanlan.zhihu.com/p/65447367）：
$$g_{{\theta }^{\prime }}\star x\approx {\theta }_0^{\prime }x+{\theta }_1^{\prime }(L-I_N)x$$
论文里面设定的拉普拉斯矩阵：$L=I_N-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$，代入上面得原文公式6
$$g_{{\theta }^{\prime }}\star x\approx {\theta }_0^{\prime }x-{\theta }_1^{\prime }{D}^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}x$$
这个时候两个参数不一样（而且二者没有约束），一个是参数量大，二是容易过拟合，因此都设置成一样的。In practice, it can be beneficial to constrain the number of parameters further to address overfitting and to minimize the number of operations (such as matrix multiplications) per layer.
设置${\theta }_0^{\prime }=-{\theta }_1^{\prime }=\theta$，得到公式7：
$$g_{{\theta }^{\prime }}\star x\approx \theta (I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}})x$$
由于$I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$的特征值取值范围是[0,2]，这个范围不好，因为这样会造成梯度消失或者爆炸（这也是为什么很多NN网络要加normalization操作），因此原文加了一个：renormalization trick：
$$I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\to {\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$$
其中：
$$\tilde{A}=A+I_N,{\tilde{D}}_{ii}=\sum _j{\tilde{A}}_{ij}$$
因此，得到了最后的公式8：
$$Z={\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}X\Theta$$

实验设置和结果分析

数据集

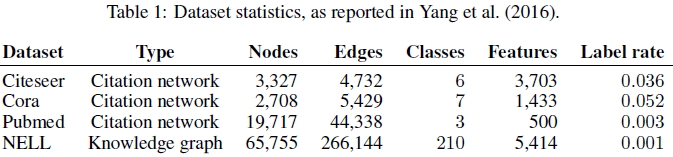
由于是半监督学习，最后一列是带有label的节点的比例。
Cora这个应该比较熟悉了
最后一个是知识图谱的数据集，是bipartite graph（二分图）

节点分类任务

消息传递方式比较

运行效率

总结

关键点

• 模型结构
• 图的拉普拉斯矩阵
• Chebyshev多项式卷积核
• 频域分析

创新点

• 空域和频域联系
• 1st-Chebyshev卷积核实用（就是k=0和k=1的情况）
• 半监督框架+ layer-wise GCN

启发点

• GCN实用化的开始，1st-ChebyshevGCN
• 将chebyshev多项式卷积核截断近似为K=1
• 演化出很多GCN为基础的模型，如RGCN等
• 半监督框架的消息传递策略融合了点的特征和图结构
• 与GNN常用框架之间的联系
• GCN、GAT、GraphSAGE都是非常重要的模型，也是经典baseline

代码复现

https://github.com/tkipf/pygcn
数据集就用cora。

train.py

from __future__ import division
from __future__ import print_functionimport time
import argparse
import numpy as npimport torch
import torch.nn.functional as F
import torch.optim as optimfrom pygcn.utils import load_data, accuracy
from pygcn.models import GCN# Training settings
parser = argparse.ArgumentParser()
# 禁用CUDA训练
parser.add_argument('--no-cuda', action='store_true', default=False,help='Disables CUDA training.')
#是否在训练过程中进行验证
parser.add_argument('--fastmode', action='store_true', default=False,help='Validate during training pass.')
#随机种子
parser.add_argument('--seed', type=int, default=42, help='Random seed.')
#epoch数量
parser.add_argument('--epochs', type=int, default=200,help='Number of epochs to train.')
#学习率
parser.add_argument('--lr', type=float, default=0.01,help='Initial learning rate.')
#权重衰减
parser.add_argument('--weight_decay', type=float, default=5e-4,help='Weight decay (L2 loss on parameters).')
#隐藏层大小
parser.add_argument('--hidden', type=int, default=16,help='Number of hidden units.')
#dropout参数
parser.add_argument('--dropout', type=float, default=0.5,help='Dropout rate (1 - keep probability).')args = parser.parse_args()
#jupyter要用下面这句
#args=parser.parse_args(args=[])
args.cuda = not args.no_cuda and torch.cuda.is_available()#产生随机数种子
np.random.seed(args.seed)
torch.manual_seed(args.seed)
if args.cuda:torch.cuda.manual_seed(args.seed)# Load data
#与GAT差不多
#加载数据
#adj:adj样本关系的对称邻接矩阵的稀疏张量
#features：样本特征张量
#labels：样本标签
#idx train：训练集索引列表
#idx val：验证集索引列表
#idx_test：测/试集索引列表
adj, features, labels, idx_train, idx_val, idx_test = load_data()# Model and optimizer
#模型和优化器# GCN模型
# nfeat输入单元数，shape[1]表示特征矩阵的维度数（列数）
# nhid中间层单元数量
# nclass输出单元数，即样本标签数=样本标签最大值+1，cora里面是7
# dropout参数
model = GCN(nfeat=features.shape[1],nhid=args.hidden,nclass=labels.max().item() + 1,dropout=args.dropout)# 构造一个优化器对象0ptimizer，用来保存当前的状态，并能够根据计算得到的梯度来更新参数
# Adam优化器
# 1r学习率
# weight_decay权重衰减（L2惩罚）
optimizer = optim.Adam(model.parameters(),lr=args.lr, weight_decay=args.weight_decay)#gpu执行下面代码
if args.cuda:model.cuda()features = features.cuda()adj = adj.cuda()labels = labels.cuda()idx_train = idx_train.cuda()idx_val = idx_val.cuda()idx_test = idx_test.cuda()def train(epoch):#取当前时间t = time.time()#train的时候使用dropout，测试的时候不使用dropout#pytorch里面eval()固定整个网络参数，没有dropoutmodel.train()#把梯度置零，也就是把loss关于weight的导数变成0optimizer.zero_grad()#执行GCN中的forward前向传播output = model(features, adj)#最大似然/log似然损失函数，idx_train是140（0~139）#nll loss:negative log likelihood loss #https://www.cnblogs.com/marsggbo/p/10401215.htmlloss_train = F.nll_loss(output[idx_train], labels[idx_train])#计算准确率acc_train = accuracy(output[idx_train], labels[idx_train])#反向传播loss_train.backward()#梯度下降optimizer.step()if not args.fastmode:# Evaluate validation set performance separately,# deactivates dropout during validation run.model.eval()#EVAL不启用bn和dropoutoutput = model(features, adj)#EVAL的最大似然/log似然损失函数，idxval是300（200-499）loss_val = F.nll_loss(output[idx_val], labels[idx_val])#EVAL的准确率acc_val = accuracy(output[idx_val], labels[idx_val])#正在送代的epoch数#训练集损失函数值#训练集准确率#验证集损失函数值#验证集准确率#运行时间print('Epoch: {:04d}'.format(epoch+1),'loss_train: {:.4f}'.format(loss_train.item()),'acc_train: {:.4f}'.format(acc_train.item()),'loss_val: {:.4f}'.format(loss_val.item()),'acc_val: {:.4f}'.format(acc_val.item()),'time: {:.4f}s'.format(time.time() - t))#测试，参考EVAL注释即可
def test():model.eval()output = model(features, adj)loss_test = F.nll_loss(output[idx_test], labels[idx_test])acc_test = accuracy(output[idx_test], labels[idx_test])print("Test set results:","loss= {:.4f}".format(loss_test.item()),"accuracy= {:.4f}".format(acc_test.item()))# Train model
t_total = time.time()
#根据设置epoch数量进行训练
for epoch in range(args.epochs):train(epoch)
print("Optimization Finished!")
print("Total time elapsed: {:.4f}s".format(time.time() - t_total))# Testing
test()

util.py

import numpy as np
import scipy.sparse as sp
import torchdef encode_onehot(labels):classes = set(labels)#identity创建方矩阵#字典key为labe1的值，value为矩阵的每一行classes_dict = {c: np.identity(len(classes))[i, :] for i, c inenumerate(classes)}#get函数得到字典key对应的value#map()会根据提供的函数对指定序列做映射#第一个参数 function 以参数序列中的每一个元素调用function函数，返回包含每次 function 函数返回值的新列表#map(lambdax:x**2，[1，2，3，4，5])#output:[1，4，9，16，25]labels_onehot = np.array(list(map(classes_dict.get, labels)),dtype=np.int32)return labels_onehotdef load_data(path="./data/cora/", dataset="cora"):"""Load citation network dataset (cora only for now)"""print('Loading {} dataset...'.format(dataset))#content file的每一行的格式为：<paper_id> <word attributes><class_label>#三个字段的index分别对应0，1：-1，-1#feature为第二列到倒数第二列，labe1s为最后一列idx_features_labels = np.genfromtxt("{}{}.content".format(path, dataset),dtype=np.dtype(str))#储存为csr型稀疏矩阵features = sp.csr_matrix(idx_features_labels[:, 1:-1], dtype=np.float32)labels = encode_onehot(idx_features_labels[:, -1])# build graph# cites file的每一行格式为：<cited paper ID：被引用文章编号><citing paper ID：引用文章的编号># 根据前面的contents与这里的cites创建图，算出edges矩阵与adj矩阵idx = np.array(idx_features_labels[:, 0], dtype=np.int32)# 由于文件中节点并非是按顺序排列的，因此建立一个编号为0-(node_size-1)的哈希表idx_map# 哈希表中每一项为o1d id:number，即节点id对应的编号为numberidx_map = {j: i for i, j in enumerate(idx)}#edges_unordered为直接从边表文件中直接读取的结果，是一个(edge_num，2)的数组，每一行表示一条边两个端点的idxedges_unordered = np.genfromtxt("{}{}.cites".format(path, dataset),dtype=np.int32)#flatten：降维，返回一维数组，这里把是1*2的数组展开为1维数组#边的edges unordered中存储的是端点id，要将每一项的o1d id换成编号number（新编号）#在idx_map中以idx作为键查找得到对应节点的编号，reshape成与edges_unordered形状一样的数组edges = np.array(list(map(idx_map.get, edges_unordered.flatten())),dtype=np.int32).reshape(edges_unordered.shape)#根据coo矩阵性质，这一段的作用是：网络有多少条边，邻接矩阵就有多少个1，#所以先创建一个长度为edge_num的全1数组，每个1的填充位置就是一条边中两个端点的编号，#即edges[:,0]，edges[：,1]，矩阵的形状为(node_size，node_size)adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])),shape=(labels.shape[0], labels.shape[0]),dtype=np.float32)# build symmetric adjacency matrix# 对于无向图，邻接矩阵是对称的。上一步得到的adj是按有向图构建的，转换成无向图的邻接矩阵需要扩充成对称矩阵# 将i->j与j->i中权重最大的那个，作为无向图的节点节点j的边权。# 原文NELL数据集用了这个操作# https://blog.csdn.net/Eric_1993/article/details/102907104adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)features = normalize(features)# eye创建单位矩阵，第一个参数为行数，第二个为列数# normalize对应论文里A^=（D~）-1A~这个公式# +eye,对应公式A-=A+I_Nadj = normalize(adj + sp.eye(adj.shape[0]))#分别构建训练集、验证集、测试集，并创建特征矩阵、标签向量和邻接矩阵的tensor，用来做模型的输入idx_train = range(140)idx_val = range(200, 500)idx_test = range(500, 1500)features = torch.FloatTensor(np.array(features.todense()))labels = torch.LongTensor(np.where(labels)[1])#邻接矩阵（coo矩阵）转为torch的稀疏tensor处理adj = sparse_mx_to_torch_sparse_tensor(adj)idx_train = torch.LongTensor(idx_train)idx_val = torch.LongTensor(idx_val)idx_test = torch.LongTensor(idx_test)return adj, features, labels, idx_train, idx_val, idx_testdef normalize(mx):"""Row-normalize sparse matrix"""#mx是邻接矩阵，传进来之后，先做行和，得到每一个节点的度就是得到D这个矩阵rowsum = np.array(mx.sum(1))#然后对度矩阵求倒数，得到D^-1（这里不是矩阵，是数组）r_inv = np.power(rowsum, -1).flatten()#如果某一行全为0，则r inv算出来会等于无穷大，将这些行的rinv置为0r_inv[np.isinf(r_inv)] = 0.#用度的一维数组构建对角元素为r_inv的对角矩阵r_mat_inv = sp.diags(r_inv)#再和邻接矩阵mx做点乘mx = r_mat_inv.dot(mx)return mxdef accuracy(output, labels):#使用type as（tesnor）将张量转换为给定类型的张量preds = output.max(1)[1].type_as(labels)#记录等于preds的label eq:equalcorrect = preds.eq(labels).double()correct = correct.sum()#预测正确数量/总数return correct / len(labels)def sparse_mx_to_torch_sparse_tensor(sparse_mx):"""Convert a scipy sparse matrix to a torch sparse tensor."""sparse_mx = sparse_mx.tocoo().astype(np.float32)indices = torch.from_numpy(np.vstack((sparse_mx.row, sparse_mx.col)).astype(np.int64))values = torch.from_numpy(sparse_mx.data)shape = torch.Size(sparse_mx.shape)#只用记录有值的索引，值，以及shapereturn torch.sparse.FloatTensor(indices, values, shape)

model.py

import torch.nn as nn
import torch.nn.functional as F
from pygcn.layers import GraphConvolutionclass GCN(nn.Module):# nfeat输入单元数，shape[1]表示特征矩阵的维度数（列数）# nhid中间层单元数量# nclass输出单元数，即样本标签数=样本标签最大值+1，cora里面是7# dropout参数def __init__(self, nfeat, nhid, nclass, dropout):super(GCN, self).__init__()# nfeat输入，nhid第一层输出，第二层的输入，nclass输出self.gc1 = GraphConvolution(nfeat, nhid)self.gc2 = GraphConvolution(nhid, nclass)self.dropout = dropout#x是输入特征，adj是邻接矩阵def forward(self, x, adj):#第一层加非线性函数和dropoutx = F.relu(self.gc1(x, adj))x = F.dropout(x, self.dropout, training=self.training)##gc2层x = self.gc2(x, adj)#输出为输出层做1og_softmax变换的结果，dim表示1og_softmax将计算的维度return F.log_softmax(x, dim=1)

layer.py

import mathimport torchfrom torch.nn.parameter import Parameter
from torch.nn.modules.module import Moduleclass GraphConvolution(Module):"""Simple GCN layer, similar to https://arxiv.org/abs/1609.02907"""def __init__(self, in_features, out_features, bias=True):super(GraphConvolution, self).__init__()#输入特征self.in_features = in_features#输出特征self.out_features = out_features#模型要学习的权重W，in_featuifes * out_featuresself.weight = Parameter(torch.FloatTensor(in_features, out_features))#是否设置biasif bias:self.bias = Parameter(torch.FloatTensor(out_features))else:self.register_parameter('bias', None)self.reset_parameters()def reset_parameters(self):#weight=[in features,out features]#size(1)是指out features，stdv=1/sqrt(out features)计算标准差stdv = 1. / math.sqrt(self.weight.size(1))self.weight.data.uniform_(-stdv, stdv)if self.bias is not None:self.bias.data.uniform_(-stdv, stdv)def forward(self, input, adj):#计算A*X*W，非线性函数ReLU在model里面加#input和self.weight矩阵相乘#先算support=X*Wsupport = torch.mm(input, self.weight)#spmm()是稀疏矩阵乘法，减小运算复杂度#计算A*X*W=A*先算supportoutput = torch.spmm(adj, support)#判断是否需要返回偏置if self.bias is not None:return output + self.biaselse:return outputdef __repr__(self):return self.__class__.__name__ + ' (' \+ str(self.in_features) + ' -> ' \+ str(self.out_features) + ')'

作业

【思考题】将实践的代码与论文中的公式对应起来，回顾模型是如何实现的。
【代码实践】为算法设置不同的参数，GCN的层数、hidden_size的大小对模型效果的影响。
【总结】总结GCN的关键技术以及如何代码实现。