斐波那契数列数列是我们学习递归的入门问题,是一种非常经典的题型,也衍生出了一些更复杂的题型,这一节就让我们彻底理解斐波那契数列系列问题。
一、概念介绍
1、什么是斐波那契数列?
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N)
2、怎么定义斐波那契数列
斐波那契数列指的是这样一个数列:1,1,2,3,5,8,13,21,34,55,89…
递推公式
斐波那契数列:1,1,2,3,5,8,13,21,34,55,89…
斐波纳契数列以如下被以递归的方法定义:
f[0] = 0, f[1] = 1;f[n] = f[n -1] + f[n - 2](n >= 2)
这个数列从第三项开始,每一项都等于前两项之和。
显然这是一个线性递推数列。
4、斐波那契数列系列问题详解
最入门的斐波那契数列问题

分析题意:是最基本的斐波那契数列问题,问的就是第n个斐波那契数列的值是多少并且输出出来。
根据我们的递推方程 : f[0] = 0, f[1] = 1;f[n] = f[n -1] + f[n - 2](n >= 2)即可求出
递归示意图:
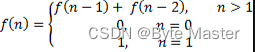
1. 递归。该递归属于多分支递归,会造成栈溢出。
//递归
#include<stdio.h>int Fib(int n)
{if (n == 1 || n == 2)//数列前两项{return 1;}else//从第三项开始{return Fib(n - 1) + Fib(n - 2);}return 0;
}
int main()
{int n = 0;scanf("%d", &n);//输入一个数int ret = Fib(n);//计算斐波那契数列printf("%d\n", ret);//打印结果return 0;
}2)非递归。非递归较递归效率更高,避免了重复计算的时间和空间。
//非递归
int main()
{int n = 0;printf("请输入一个整数:");scanf("%d", &n);if (n == 1 || n == 2) {return 1;}else {int f1 = 1;int f2 = 1;int f3 = -1;for (int i = 3; i <= n; i++) {f3 = f1 + f2;f1 = f2;f2 = f3;}printf("该整数的Fib数列为%d", f3);}return 0;
}3)数组。
//数组法
#include<stdio.h>int Fib(int n)
{int i;int arr[100] = { 0,1,1 };for (i = 2; i <= n; i++)//从第一项开始{arr[i] = arr[i - 1] + arr[i - 2];}return arr[n];
}
int main()
{int n;scanf("%d", &n);printf("%d", Fib(n));return 0;
}