题目一
此题用暴力枚举做过(80分)现如今终于用二维前缀和做到满分。

试题编号: 202309-2
试题名称: 坐标变换(其二)
时间限制: 2.0s
内存限制: 512.0MB
问题描述:
问题描述

样例输入:
10 5
2 0.59
2 4.956
1 0.997
1 1.364
1 1.242
1 0.82
2 2.824
1 0.716
2 0.178
2 4.094
1 6 -953188 -946637
1 9 969538 848081
4 7 -114758 522223
1 9 -535079 601597
8 8 159430 -511187
样例输出
-1858706.758 -83259.993
-1261428.46 201113.678
-75099.123 -738950.159
-119179.897 -789457.532
114151.88 -366009.892
题目分析(个人理解)
- 其实对于二维数据的存储和处理非常想用numpy的,但是考试的IOI机子不支持,只能用常规的二维列表存储。
- 使用一个列表an[]存每一步操作之后的参数,由于对于一个坐标有两种操作,一种拉伸一种旋转,所以是个二维列表,第一维度表示查询的序号。第二维度表示该查询的具体内容(拉伸多少倍或旋转多少度),因此第二维度的第一个元素用1初始化(表示拉伸,可直接乘拉伸倍数即可)第二个元素用0初始化(表示旋转,只需要做加法加即可)。
- 注意规则,**i和j是开始查询数到结束,经历的操作是从i到j。有两种思想,第一种暴力穷举,每输入一个要处理的坐标就进行一次遍历,因此超时只能80分,第二种二维前缀和的思想,每输入一行查询操作就假想已经执行并且存入数组,这样在后续执行的时候只需要切片即可,大大降低时间复杂度。
- 如何截取前缀和的一部分?不难发现对于拉伸倍数只需要用除法判断从i到j进行每一步查询之后总的拉伸倍数即可,对于旋转,只需用末减初即可判断最后到底拉伸了多少最后按照公式计算即可。
- 上代码!!!
import mathn,m = map(int,input().split())#设置前缀积的初始化
an = []
an.append([1,0])for i in range(n):#存入执行每一步之后的拉伸和旋转参数kind,act = input().split()if kind == '1':#如果是拉伸temp1 = an[i][0]*float(act)temp2 = an[i][1]an.append([temp1,temp2])else:#如果是旋转temp2 = an[i][1]+float(act)temp1 = an[i][0]an.append([temp1, temp2])for v in range(m):#开始切片操作执行i,j,x,y = map(int,input().split())k = an[j][0] / an[i-1][0]#对于拉伸做除法c = an[j][1] - an[i-1][1]#对于旋转做减法dx = k*(x*math.cos(c) - (y*math.sin(c)))dy = k*(x*math.sin(c) + (y*math.cos(c)))print("{:.3f} {:.3f}".format(dx,dy))题目二
【问题描述】给定一个N×M的矩阵A,请你统计有多少个子矩阵 (最小1×1,最大N×M) ,满足子矩阵中所有数的和不超过给定的整数K?
【输入格式】第一行包含三个整数N, M和K,之后N行每行包含M个整数,代表矩阵A
【样例输入】
3 4 10
1 2 3 4
5 6 7 8
9 10 11 12
【样例输出】
19
【评测用例规模与约定】
30%的数据,N, M≤20 5分
70%的数据,N, M≤100 10分
100%的数据,1≤N, M≤500 15分
0≤Ai j≤1000; 1≤K≤250000000
题目分析(个人理解)
- “二维前缀和”,定义s[][]:
s[i][j]表示子矩阵[1, 1] ~ [i, j]的和
(1)预计算出s[][],然后快速计算二维子区间和:
(2)阴影子矩阵[i1, j1] ~ [i2, j2]区间和,等于:
s[i2][j2] - s[i2][j1-1] - s[i1-1][j2] + s[i1-1][j1-1]
其中s[i1-1][ j1-1]被减了2次,需要加回来1次 - 本题统计二维子矩阵和≤k的数量,而不用具体指出是哪些子矩阵,可以用尺取法优化。
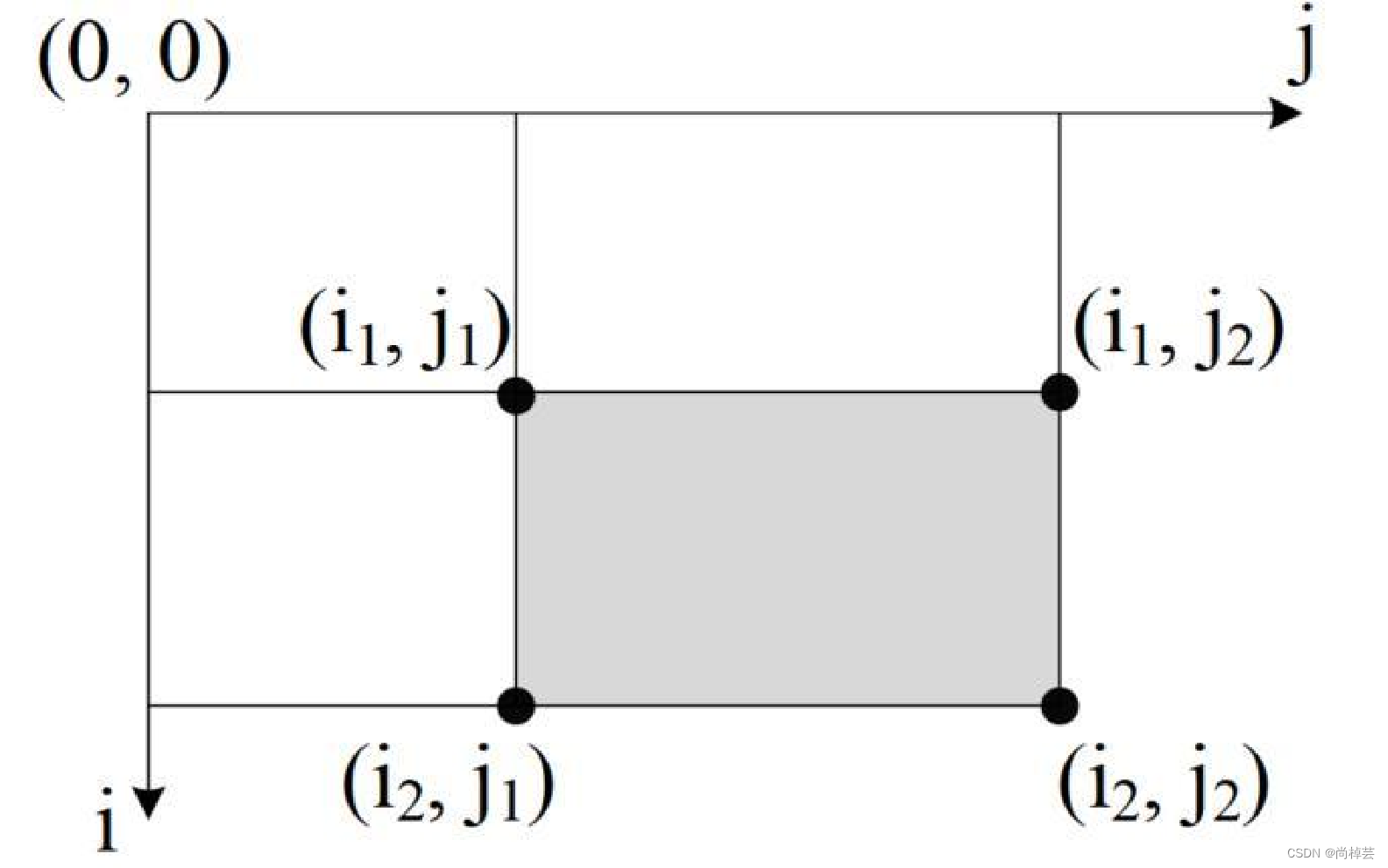
以一维区间和为例,查询有多少子区间[j1, j2]的区间和s[j2] - s[j1] ≤ k。

若s[j2] - s[j1] ≤ k,那么在子区间[j1, j2]上,有j2 - j1+1个子区间满足≤ k。用同向扫描的尺取法,用滑动窗口[j1, j2]遍历,复杂度降为O(n)。
对于二维,矩阵的行子区间和仍用2重暴力遍历只把列区间和用尺取法优化。
3. 上代码!!!
n, m, k = map(int, input().split())
a = [[0] for i in range(n)]
a.insert(0,[0]*(m+1))
for i in range(1,n+1): #从a[1][1]开始,读矩阵a[i].extend(map(int, input().split()))
s = [[0]*(m+1) for i in range(n+1)]
for i in range(1,n+1):for j in range(1,m+1):s[i][j] = s[i-1][j] + a[i][j]
ans = 0
for i1 in range(1,n+1):for i2 in range(i1,n+1):j1=1; z=0for j2 in range(1,m+1):z += s[i2][j2]-s[i1-1][j2] while z>k: z -= s[i2][j1]-s[i1-1][j1]j1 += 1 ans += j2-j1+1
print(ans)
总结