本文详细的推导了二值交叉熵(BCE)和二值交叉熵损失函数(BCE Loss)之间的关系。

一、 理论基础

$A:=f(\cdot )$ 表示$A$定义为$f(\cdot )$，这是人们为了某些目的而将$A$定义成$f(\cdot )$的，有意义的定义往往能揭示一些规律。

1. 信息量

对于事件$x$，假设它的信息量表示为$I(x)$，它发生的概率表示为$p(x)$。

基于我们的常识可以知道：

1. 一个事件$x_i$发生的概率越小，它包含的信息量$I(x_i)$应该越大$=>I$应该和$p$成反比$=>$即$I$和$\frac{1}{p}$成正比
2. 两个事件$x_i,x_j$的信息量$I(x_i)+I(x_j)$相加，应该和这两个事件同时发生有关（注意：两个事件同时发生的概率等于两个事件的概率之积$p(x_i)p(x_j)$）$=>I$应该能把加法转换为乘法$=>$可用$log$实现

基于上面两个性质，可以有$I(x):=log\frac{1}{p(x)}$ ，log的底取任何>1的值其实都没关系，但为了让它更有意义，通常取$2$为底，因为这样，就能使得抛硬币正面朝上这样只有$\frac{1}{2}$ 概率的事件的信息量刚好为1，并且可以赋予其"比特"的单位（注意，单位也是定义的，人们会把一些有意义的事情给上单位）。所以说，抛硬币正面朝上的信息量为1比特。

所以，最终定义信息量为：
$$I(x):=lo{g}_2\frac{1}{p(x)}=-lo{g}_{2}p(x)$$

2. 熵（也叫香农熵）

熵这个概念是针对一个事件集合$X$而定义的（即有一系列事件$x\in X$），

熵定义为这些事件携带信息量的平均值（也叫期望）。所以有：
$$H(p(x)):=\sum _{x\in X}p(x)I(x)=-\sum _{x\in X}p(x)lo{g}_{2}p(x)$$
或简写版：
$$H(p):=\sum p_x{I}_x=-\sum p_{x}lo{g}_2{p}_x$$
这样，熵越大，表示这个系统包含的信息越多，系统越不稳定。

熵越小，表示这个系统包含的信息越少，系统越稳定。

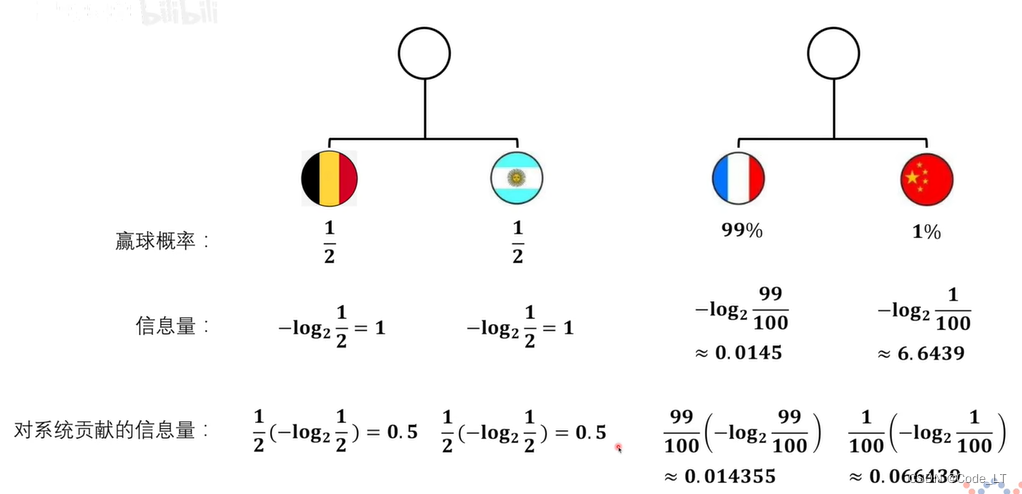
如上图所示，中国和法国比赛悬念比较小，所以信息量少，结果比较稳定。（虽然中国赢了有更大的信息量，但发生的概率太小，整体基本上是法国赢）

而德国对荷兰的比赛则55开，比较不稳定，谁最终夺冠是个信息量很大的事。

所以德国VS荷兰这个系统的熵>法国VS中国的熵

3. 交叉熵

对于事件$x$，
假设它发生的真实概率（ground truth probability）表示为$p(x)$
假设它的观测概率为$q(x)$（即通过多次试验得到的概率或者通过算法预测出来的概率）

则交叉熵定义为：
$$H(p(x),q(x)):=\sum _{x\in X}p(x)I^q(x)=-\sum _{x\in X}p(x)lo{g}_{2}q(x)$$
或简写版：
$$H(p,q):=\sum p_x{I}_x^q=-\sum p_{x}lo{g}_2{q}_x$$

$I^q(x)$表示以$q$为概率的信息量。

举个例子：
假设抛硬币正面为$h$,反面为$t$。我们知道真实概率$p(h)=p(t)=0.5$。
现在有两枚硬币，由于粘了不同程度的泥土导致抛出的概率不一样。通过实验，得到:

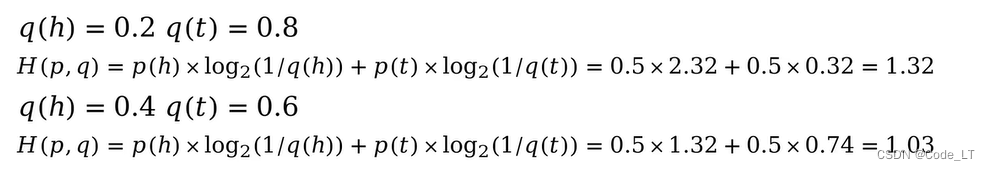
这里，我们就可以看出一点点门道了，即观测概率$q$越接近真实概率$p$。交叉熵相对越小。而这个结论是可以被证明的（见后面的KL散度）。
简化版

4. KL散度（或相对熵）

KL散度定义为交叉熵和香农熵的差。
$$\begin{array}{rl}D(p(x)||q(x))=H(p(x),q(x))-H(p(x))& =\sum _{x\in X}p(x)I^q(x)-\sum _{x\in X}p(x)I(x)\\ & =\sum _{x\in X}p(x)lo{g}_2\frac{1}{q(x)}-\sum _{x\in X}p(x)lo{g}_2\frac{1}{p(x)}\\ & =\sum _{x\in X}p(x)lo{g}_2\frac{p(x)}{q(x)}\end{array}$$
简写版：
$$\begin{array}{rl}D(p||q)=H(p,q)-H(p)& =\sum p_x{I}_x^q-\sum p_x{I}_x\\ & =\sum p_{x}lo{g}_2\frac{1}{q_x}-\sum p_{x}lo{g}_2\frac{1}{p_x}\\ & =\sum p_{x}lo{g}_2\frac{p_x}{q_x}\end{array}$$

性质1：

$D(p||q)\ge 0$ 当且仅当$q=p$时等号成立。
证明:吉布斯不等式

性质2：

$D(p||q)\ne D(q||p)$

性质3：

由于$H(p)$是个常量，q是一个变量，通常可表示为函数$f(\theta )$，所以通过选取不同$q_{\theta }$（简便起见，这么写，不代表$\theta$是事件）最小化$D(p||q_{\theta })$等价于最小化$H(p,q_{\theta })$，即：
$${▽}_{\theta }D(p||q_{\theta })={▽}_{\theta }H(p,q_{\theta })-{▽}_{\theta }H(p)={▽}_{\theta }H(p,q_{\theta })$$

关于事件空间的误解

（注意，很多教程没有讲清楚事件空间和采样试验(见下一节） 的区别，这里拉出来强调下。）

事件空间是指$X$,即事件$x$的可取值的集合。

由于观测值样本空间只能是真实值样本空间的子集，所以不存在有些教程里说的要确定取值的问题。比如下面：

当观测值和真实值一样时：

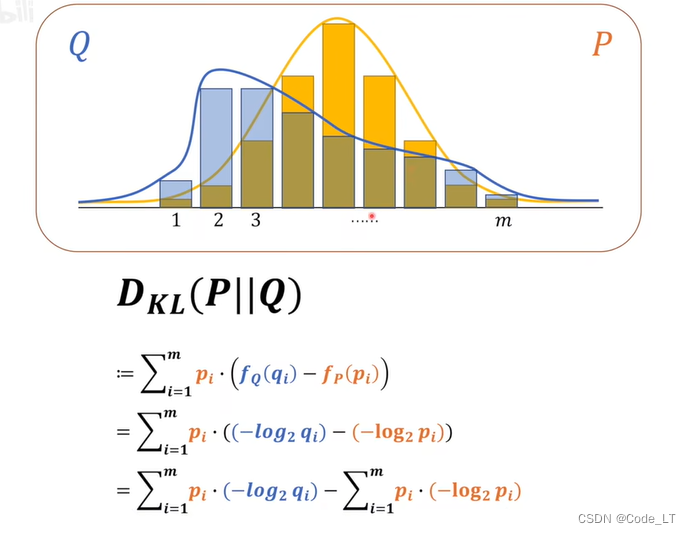
如果观测数更多：

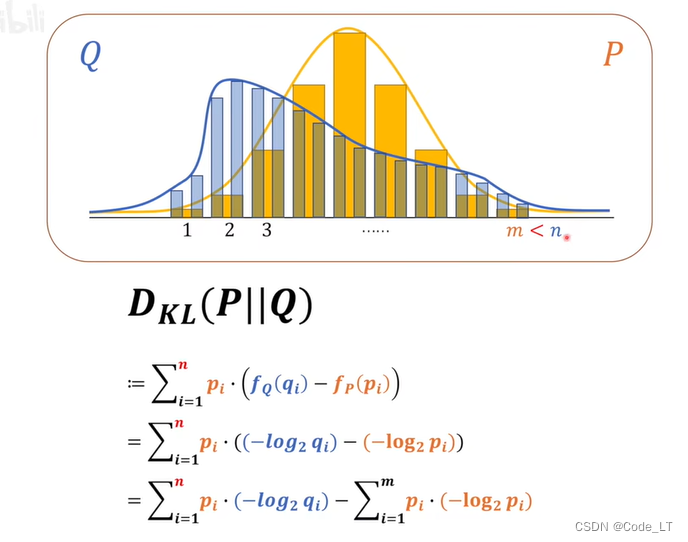
如果观测数更少：

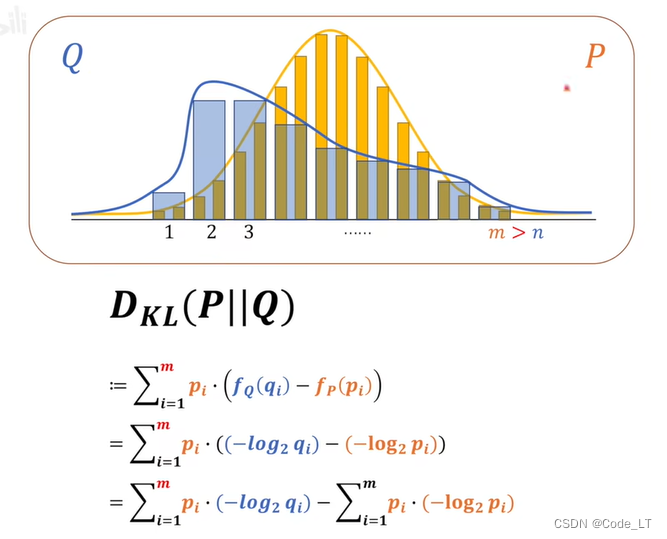
总是取事件空间更大的值。（注意上面的图在事件空间体现这块是有问题的，横轴表示事件空间。不可能出现观测值在真实值中不存在的情况，比如第一幅图，真实值只有1，它却观测到了0.4或者0.8；最后一幅图，观测到的是1，真实值从图上看又没有1。）

实际上根据公式$x\in X$这里的$X$指的是真实事件空间。对于$p$不存在的情况$i$，$p_i$取0，对于$q$不存在的情况$j$，$q_j$取0代入公式即可，不必要关注所谓的取大取小的问题。

5. 二值交叉熵(Binary Cross-Entropy，BCE)和BCE损失函数

二值交叉熵是交叉熵的一种特殊情况，即真实样本空间只有两个取值，一般来说是$[0,1]$。有$p(0)+p(1)=1,q(0)+q(1)=1$
$$\begin{array}{rl}H(p(x),q(x))=\sum _{x\in [0,1]}p(x)I^q(x)& =p(0)I^q(0)+p(1)I^q(1)\\ & =-(p(0)lo{g}_{2}q(0)+(1-p(0))lo{g}_x(1-q(0)))或=-((1-p(1))lo{g}_x(1-q(1))+p(1)lo{g}_{2}q(1))\\ & =-(p(x)lo{g}_{2}q(x)+(1-p(x))lo{g}_x(1-q(x)))\end{array}$$
其中x可取0或者1。

或简写版：
$$H(p,q)=-(p_{x}lo{g}_2{q}_x+(1-p_x)lo{g}_2(1-q_x))$$
其中$x$可取$0$或$1$。

有两点要注意：

1. H中的累加符号没有了
2. 也就是说，我们可以只关注一种结果，0或者1。

为什么我们在其他文献或者教材里看到的BCE是长下面这样呢？
$$\frac{1}{N}\sum _{i=0}^N(y_{i}lo{g}_2{\hat{y}}_i+(1-y_i)lo{g}_2(1-{\hat{y}}_i))$$
其中：$N$为采样数，$y_i$为真实标签（0或1），${\hat{y}}_i$为预测概率。

事实上，严格的来说，上面的公式并不是交叉熵，而是基于交叉熵构造的BCE损失函数，$q(x)$这个观测值或者预测值是由未知变量的函数决定的（比如sigmoid函数$q(x)(\theta )=\frac{1}{1+e^{-\theta \hat{x}}}$），假设做了N次实验，那么损失函数定义为：
$$Loss(\theta ):=\frac{1}{N}\sum _{i=0}^{N}H(p_i(x),q_i(x))=\frac{1}{N}\sum _{i=0}^{N}H(p_i(x),q_i(x)(\theta ))$$
代入BCE公式得：
$$Loss(\theta )=-\frac{1}{N}\sum _{i=0}^N(p_i(x)lo{g}_2{q}_i(x)(\theta )+(1-p_i(x))lo{g}_x(1-q_i(x)(\theta )))$$

注意这里的$i$代表的事每次实验。举个例子，假设下面有N张照片，我们预测它是不是猫。即x=1表示是猫，x=0表示不是猫。那么i就表示第i张照片。注意每个$x_i$都有两个取值。

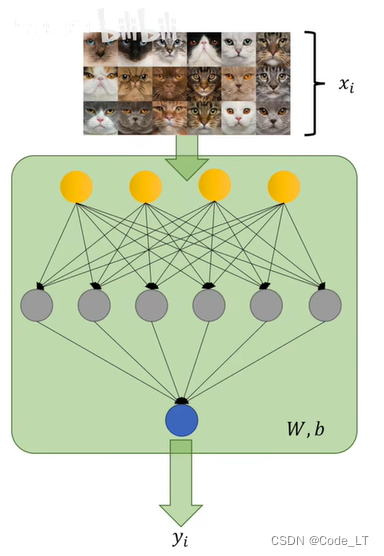
由第4节的性质3可知，最小化上面的损失函数，其实就是最小化每一个KL散度${▽}_{\theta }D(p_i||q_i(\theta ))$，
即设计这么个损失函数就是为了找最好的$\theta$使得$q_i(\theta )$在每个测试点上都能拟合真实的$p_i$。

现在只剩下疑问：原公式中只有概率，标签怎么出现到公式里的？

首先，我们要明确这里的真实事件空间是什么。

如果我们把事件定义成"a=它是1”，“b=它是0”，
类比“h=抛硬币正面朝上”和"t=抛硬币反面朝上", $p(h)=p(t)=0.5$
那么对于一张照片，它是不是猫，真实概率要么是100%要么是0%。

所以$p(a)=100\%=1$或者$p(a)=0\%=0$（刚好和标签0，1对应上）

那么，
$$\begin{array}{rl}H(p(x),q(x))& =-(p(x)lo{g}_{2}q(x)+(1-p(x))lo{g}_x(1-q(x)))\\ & =-(xlo{g}_{2}q(x)+(1-x)lo{g}_x(1-q(x)))\end{array}$$
$x$取$1$或$0$，即对应图片是不是猫的真实标签。

这样，标签的值就写进公式了。

即：
$$\begin{array}{rl}Loss(\theta )& =-\frac{1}{N}\sum _{i=0}^N(p_i(x)lo{g}_2{q}_i(x)(\theta )+(1-p_i(x))lo{g}_x(1-q_i(x)(\theta )))\\ & =-\frac{1}{N}\sum _{i=0}^N(x_{i}lo{g}_2{q}_i(x)(\theta )+(1-x_i)lo{g}_2(1-q_i(x)(\theta )))\end{array}$$

或简写版
$$\begin{array}{rlr}Loss(\theta )& =& =-\frac{1}{N}\sum _{i=0}^N(x_{i}lo{g}_2{q}_{x_i}(\theta )+(1-x_i)lo{g}_2(1-q_{x_i}(\theta )))\end{array}$$

参考

可视化理解Binary Cross-Entropy
【10分钟】了解香农熵，交叉熵和KL散度
打包理解“信息量”、“比特”、“熵”、“KL散度”
Understanding binary cross-entropy / log loss: a visual explanation
维基百科-Cross Entropy
个视频彻底搞懂交叉熵、信息熵、相对熵、KL散度、交叉熵损失、交叉熵