1、红黑树的概念

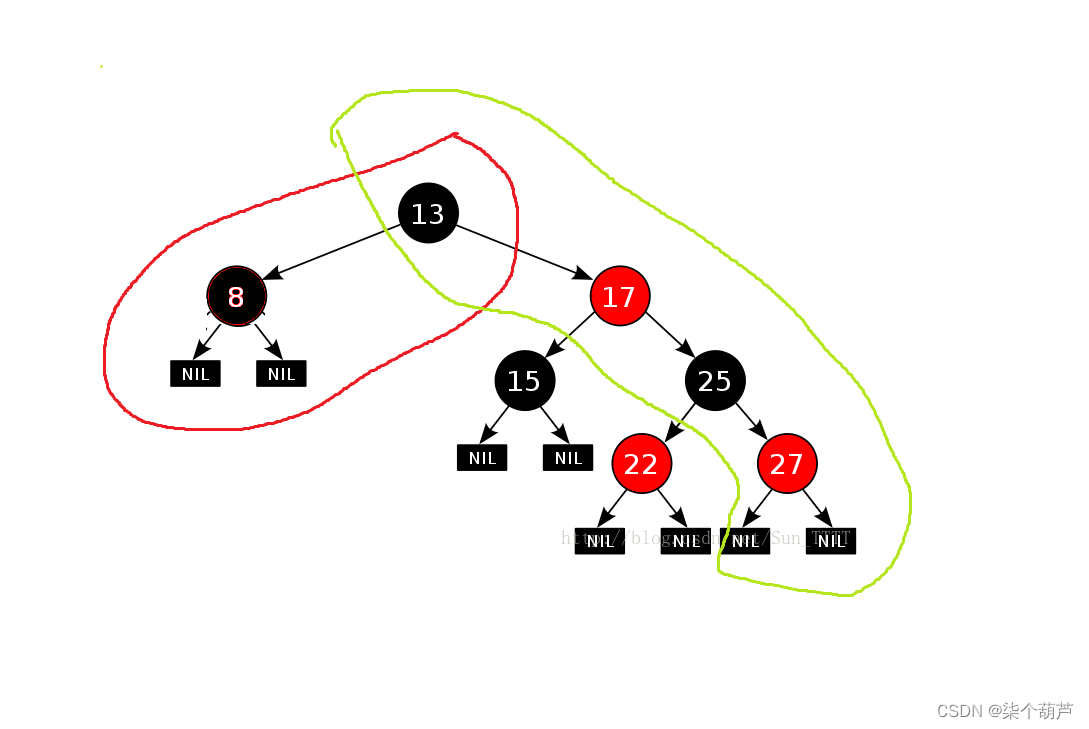
红黑树是一种二叉搜索树，但在每个节点上增加一个存储位表示节点的颜色，可以是red或black。通过对任何一条从根到叶子的路径上各个节点着色方式的限制，红黑树确保没有一条路径会比其他路径长出两倍，而是接近平衡的。

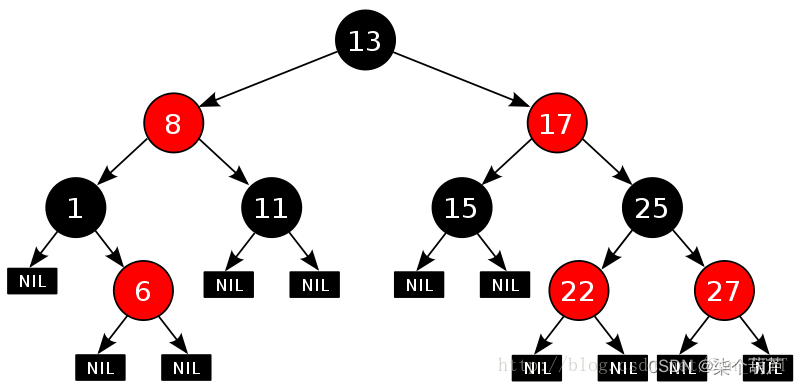
2、红黑树的性质及定义

1. 每个节点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的，则它的两个孩子节点是黑色的，没有连续的红节点
4. 对于每个节点，从该节点到其他所有后代叶节点的简单路径上，均包含相同数目的黑色节点
5. 每个叶子节点都是黑色的（此处的叶子节点是指空节点）

那么为什么红黑树就能保证最长路径中的节点个数不会超过最短路径节点个数的两倍呢？

我们可以从第3个性质和第4个性质可以得出红黑树中最长路径中的节点个数不会超过最短路径节点个数的两倍。
我们可以看一个极端场景：最短路径：全黑。最长路径：一黑一红

红黑树的定义，如下：

// 节点的颜色
enum Colour
{RED,BLACK,
};// 红黑树节点的定义
template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;// 节点的左孩子RBTreeNode<K, V>* _right;// 节点的右孩子RBTreeNode<K, V>* _parent;// 节点的双亲(红黑树需要旋转，为了实现简单给出该字段)pair<K, V> _kv;// 节点的值域Colour _col;// 节点的颜色RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};

3、红黑树的插入操作

因为新节点的默认颜色是红色，因此，如果其双亲节点的颜色是黑色，没有违反红黑树任何性质，则不需要调整，但当新插入节点的双亲节点颜色为红色时，就违反了性质三不能有连续的红节点，此时就需要对红黑树分情况来讨论了：
我们先建一个基本模型：

情况一：cur为红，p为红，g为黑，u存在且为红

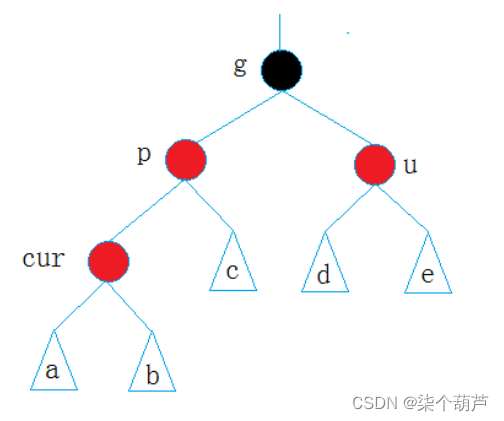
cur和p均为红，违反了性质三，此时我们需要做调整：将p,u改为黑，g改为红，如果g是根节点，调整完成后，需要将g改为黑色，如果g是子树，g一定有双亲，且g的双亲如果是红色，则需要把g当成cur，继续向上调整。

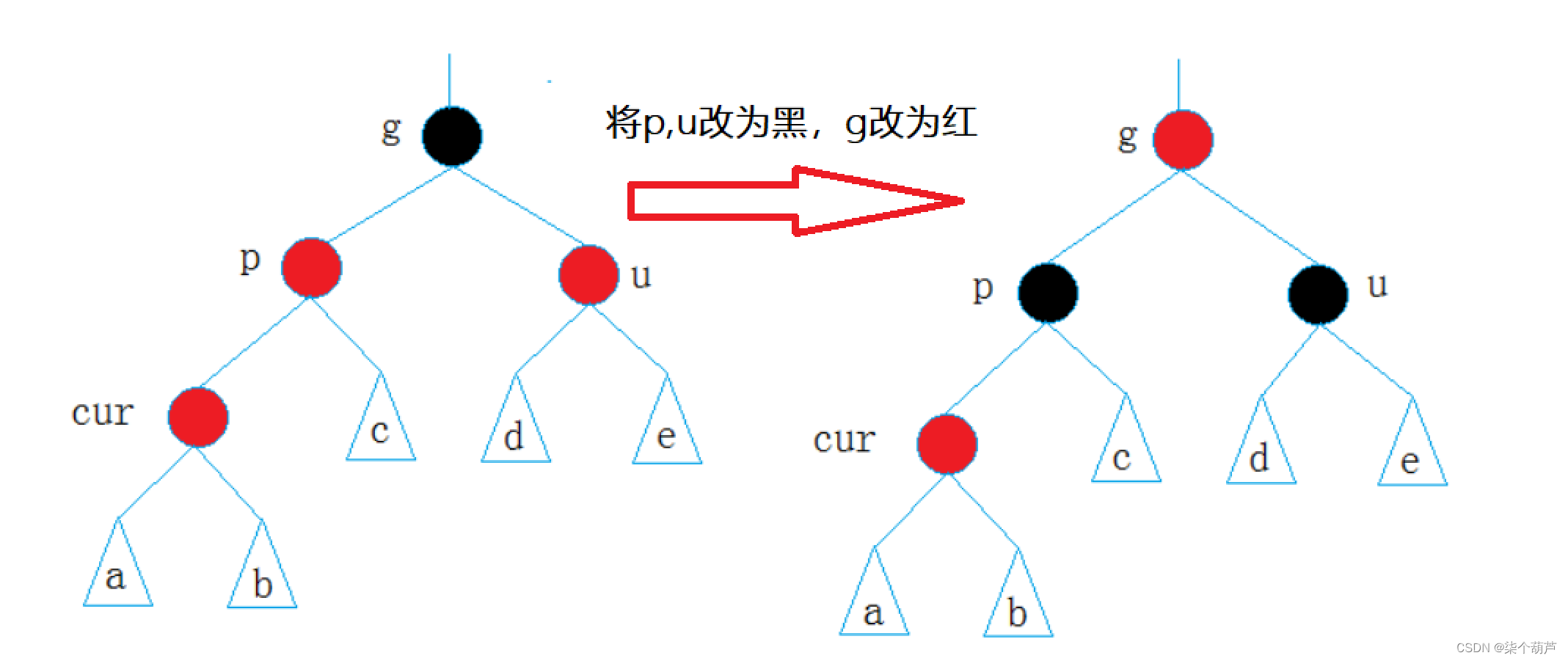
情况二: cur为红，p为红，g为黑，u不存在/u存在且为黑

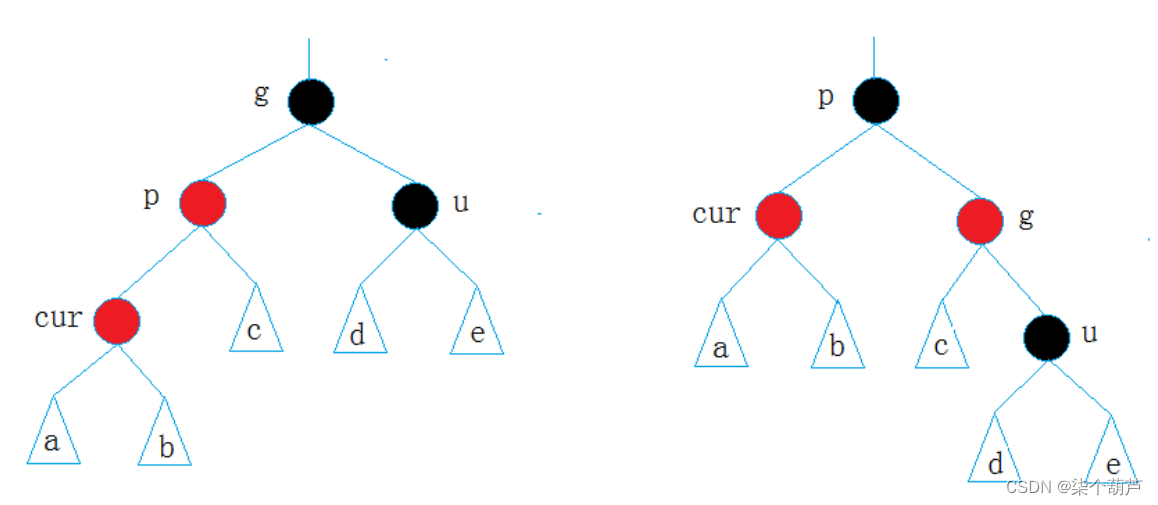
其中u有两种情况：

1、如果u不存在，则cur一定是新节点，因为如果cur不是新节点，则cur和p一定有一个节点的颜色是黑色，就不满足性质四：每条路径的黑色节点个数都相同
2、如果u存在，则其一定是黑色的，那么cur节点原来的颜色一定是黑色的，现在看到其是红色的原因是因为cur的子树在调整的过程中将cur节点的颜色由黑色改为红色

p为g的左孩子，cur为p的左孩子，则进行右单旋转
p为g的右孩子，cur为p的右孩子，则进行左单旋转
p、g变色–p变黑，g变红

情况三: cur为红，p为红，g为黑，u不存在/u存在且为黑

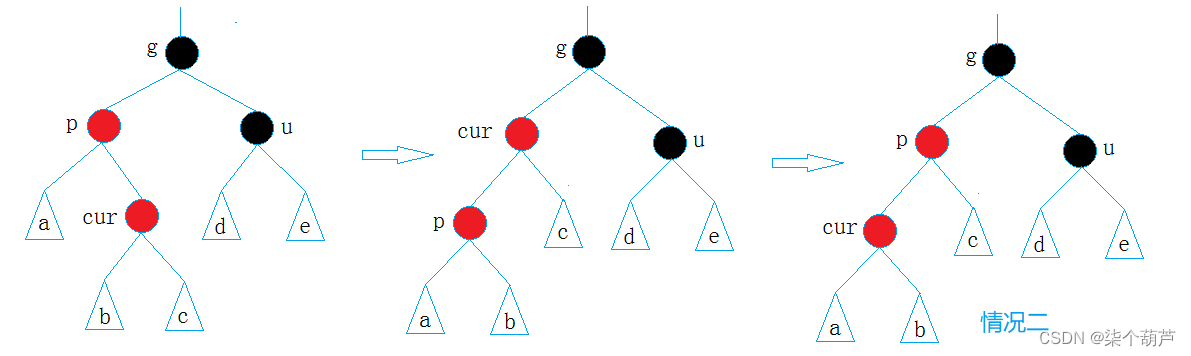
p为g的左孩子，cur为p的右孩子，则针对p做左单旋转；相反，
p为g的右孩子，cur为p的左孩子，则针对p做右单旋转
则转换成了情况2

代码展示：

template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (grandfather->_left == parent){Node* uncle = grandfather->_right;// 情况1：u存在且为红，变色处理，并继续往上处理if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 继续往上调整cur = grandfather;parent = cur->_parent;}else // 情况2+3：u不存在/u存在且为黑，旋转+变色{if (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateL(parent);RotateR(grandfather);cur->_col = BLACK;//parent->_col = RED;grandfather->_col = RED;}break;}}else // (grandfather->_right == parent){Node* uncle = grandfather->_left;// 情况1：u存在且为红，变色处理，并继续往上处理if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;// 继续往上调整cur = grandfather;parent = cur->_parent;}else // 情况2+3：u不存在/u存在且为黑，旋转+变色{if (cur == parent->_right){RotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppNode = parent->_parent;parent->_parent = subL;subL->_right = parent;if (ppNode == nullptr){_root = subL;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}
private:Node* _root = nullptr;
};