摘要:信用评分是银行等金融机构中一个关键的风险管理场景,也是贷款业务的重中之重。而特征选择是其中必不可少的数据预处理策略,通过从海量特征中提取有效特征,就可以构建更简单、准确的机器学习模型,从而提高数据挖掘性能。
通过量子计算来实现特征选择,降低数据维度,相比传统方法效率更高且能减少人工的干扰,整体提升信用评分模型效果,为金融业提供更有价值的贷款参考信息。

近年来,随着经济的发展,借款人的个人经济情况也悄然发生了巨大变化:消费者债务一路走高,银行业要寻找新的,潜在的优质借款人也越来越困难。所以特征选择在信用评分场景中起着至关重要的作用,通过筛选后续入模的特征可以提高模型的准确率和效率,并使得模型具有更好的泛化能力。
目前,玻色量子已联合北京量子信息科学研究院、光大科技、平安银行等合作伙伴,在特征选择问题上进行了深入的联合探索,并在国内首先取得了一系列重要研究成果。
2022年9月,由玻色量子创始人&CEO文凯博士、玻色量子创始人&COO马寅、光大科技大数据研究团队负责人王鹏、光大科技大数据研究团队朱德立联合撰写的“基于光量子计算的信用评分特征筛选研究报告”,在由中国电子信息产业集团有限公司主管,中国电子信息产业集团有限公司第六研究所主办的《网络安全与数据治理——量子计算应用前瞻》上成功发表🔗。这代表着玻色量子不仅率先在金融科技领域实现光量子计算场景应用商业化,还在这一领域的应用研究中成果突出。
2022年12月,我们与平安银行在“量子+金融”领域达成深入合作,基于实际金融场景及需求,共同打造量子计算的行业级应用解决方案🔗。2023年5月16日,在玻色量子的首场自研100计算量子比特相干光量子计算机“天工量子大脑”的新品发布会现场🔗,平安银行LAMBDA实验室负责人崔孝林提到,平安银行已在玻色量子的“天工量子大脑”上实现对德国信用数据集特征筛选计算的加速,在低于1ms的时间内就完成了问题求解,并且相对于传统优化算法,可以找到更低能量的可行解。这是在信用评分领域国内首个公开发表的具有量子优势的重要成果。
下面我们将给出完整真机测试报告:从特征选择问题入手,对该问题进行分析与建模,并与模拟退火、模拟器、真机测试的各类结果进行对比分析与总结。
场景介绍
在特征选择中,常用的方法包括过滤法、包装法和嵌入法等。其中,过滤法是通过对特征的统计分析、相关系数计算等方式进行筛选;包装法则是通过在特征集合中搜索,每次选出一个子集进行训练,再根据训练结果进行特征选择;嵌入法是指在模型训练过程中进行特征选择,将特征选择过程融入到模型中。
本场景采用传统信用评分的建模逻辑,对于特征选择这一环节,运用量子计算的方式进行优化,从而对整体模型效果进行提升。当特征数很大时,人工筛选难度将大大增加,而量子的方法将很好地解决这一难题。
问题分析及建模
问题分析
在传统特征选取思路中,假设从n个特征的原始集合中,我们想要选择m个特征的一个子集,用于做出信用决策。首先通过iv值筛选掉对结果影响不大的冗余特征,在此基础上选择出相关性较高的特征对,即该对特征对结果有影响但由于相关性很高,会影响建模的性能,通过人工去除其中一个来进行不断尝试,从而达到筛选特征的效果。
本案例中特征选择的过程将通过建立相应的二次无约束二值优化(Quadratic Unbounded Binary Optimization,以下简称QUBO)模型来实现,理想情况下,该模型会选择既独立又有影响力的特征。此次研究主要通过量子计算来实现特征选择,相比传统信用评分的特征选择方法,效率更高而且能减少人工的干扰。
数据及预处理
案例采用的数据是德国信用数据,其中包括20个特征(7个数字特征,13个分类特征)和一个二元分类(良好信用或不良信用)。在此基础上,采用下述数据预处理的方式:先对数据进行预处理,将分类特征进行one-hot转码,使得特征数增加为48个。
数学建模
预处理后的数据为一个m行和n列(n为特征个数)的矩阵U,每一列代表一个特征,每一行表示信用申请人的相应数据值。
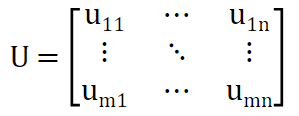
历史信用记录表示为m元素向量V:
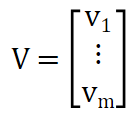
将原始数据中代表信用credit的数据值(Vi)限制为0和1,其中0表示接受,1表示拒绝信贷申请。
在后续建立QUBO模型时,需要计算特征之间的相关性及每个特征对信用V的相关性,我们采用斯皮尔曼相关性计算方法。斯皮尔曼相关系数是一个介于-1和1之间的数值,它描述了两个变量之间的相关性。当斯皮尔曼相关系数为正时,说明两个变量之间存在正相关性,即一个变量增加时另一个变量也增加;当斯皮尔曼相关系数为负时,说明两个变量之间存在负相关性,即一个变量增加时另一个变量减少;当斯皮尔曼相关系数为0时,说明两个变量之间不存在线性关系。
计算斯皮尔曼相关系数的步骤如下:
1.将两个变量的数据按照大小顺序排序,并计算它们的秩次。
2.计算每个数据的秩次差,即将两个变量的秩次相减。
3.计算每个数据的秩次差的平方,并将它们相加。
4.计算斯皮尔曼相关系数,即1减去4除以n(n^2-1),其中n是数据的数量。
从数学上讲,目标将是找到与V相关,但彼此不相关的U的列。设ρij表示矩阵U的第i列与第j列的相关性,设ρVj表示U的第j列与V的单列的相关性。为了找到“最佳”子集,引入了n个二进制变量xj,这些变量具有以下特性:

我们把这些统称为向量X,其中
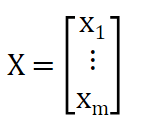
筛选最佳特征子集就是求解最小化目标函数的X的值,目标函数由两部分组成:
1.第一部分表示特征对被标记的类的影响:(这里显示的形式随着包含更多的特征而增加)
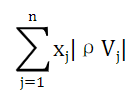
2.第二个组成部分代表了独立性:(下面所示的形式随着更多的交叉相关项的加入而增加,相关性增加,这与独立性相反。)
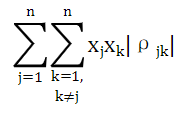
引入参数α(0≤α≤1)以表示独立性(在α=0时最大)和影响性(在α=1最大)的相对权重并得到如下的目标函数:
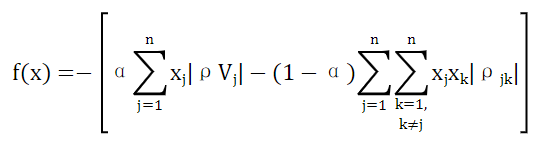
将其写为适用于QUBO模型向量乘积的形式:
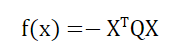
通过量子计算的方法求解向量X*,从而得到筛选后的特征子集。
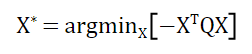
真机测试结果
“天工量子大脑”真机和传统算法对比
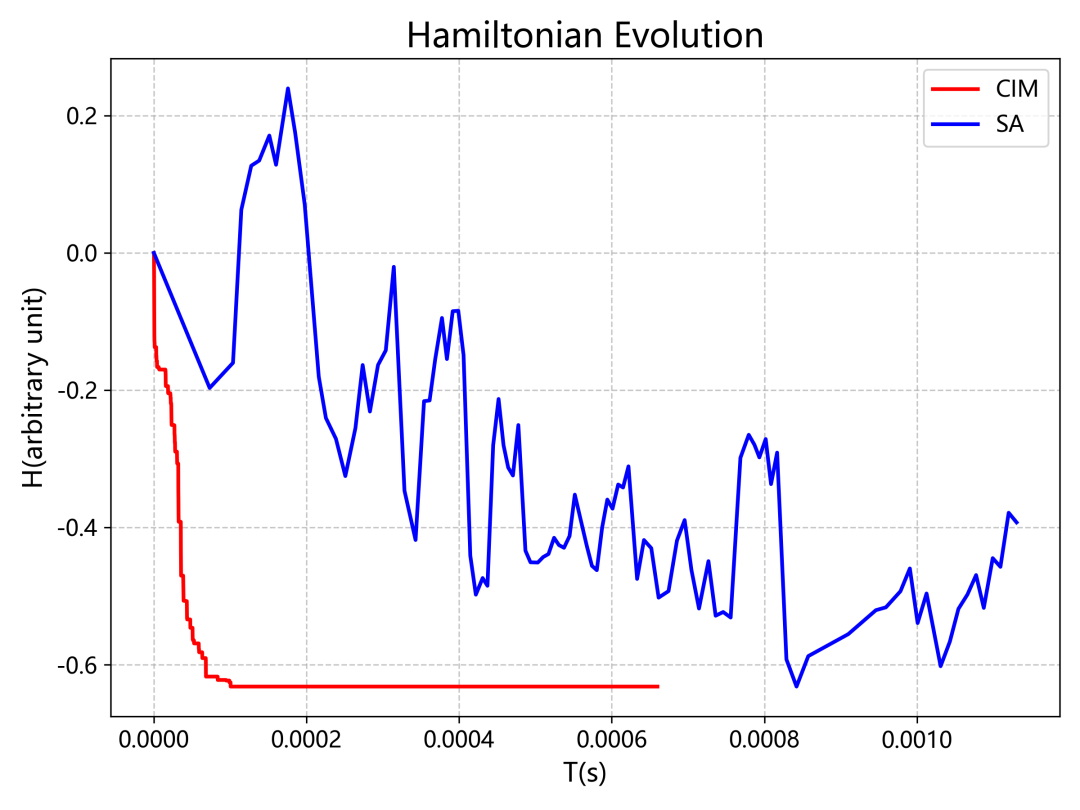
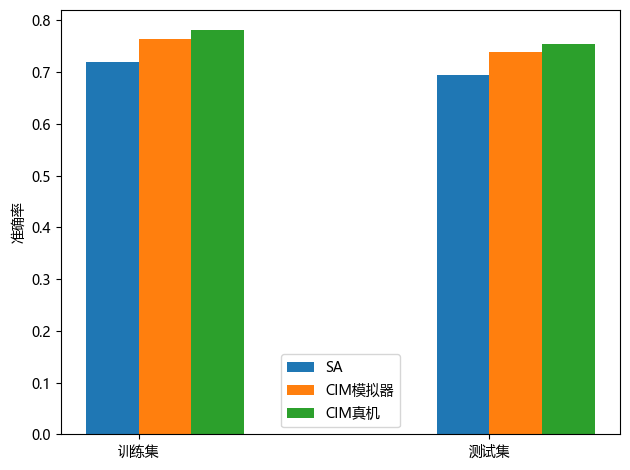
整体结论:面对同等规模的问题,量子计算机只需要不到1ms的时间,就收敛到了全局最优解,相比于在经典计算机上使用模拟退火算法求解,加速了上百倍!并且随着问题规模的逐渐增大,经典算法的耗时将显著增加,但量子计算可始终维持在毫秒量级,这种计算速度上的优势愈发明显。
同时可以看到,通过量子计算筛选出的特征集来做算法训练,依然可以保证算法的准确率,甚至有所提高,这也进一步证实了“天工量子大脑”在面对同样大规模的解空间时,更容易的找到那个“更优”的答案!
接下来,玻色量子还将启动“燎原计划”开发者平台,并持续对外开放“天工量子大脑”的真机测试,热忱欢迎更多不同领域的研究伙伴前来了解相干量子计算的原理和能力,在此基础上展开共同研发,用量子计算去解决更多真实场景中的问题,让量子计算的超强算力能真正服务于各行各业,满足未来时代对于计算的需求。