【C++高阶(三)】AVL树深度剖析模拟实现

💓博主CSDN主页:杭电码农-NEO💓
 
⏩专栏分类:C++从入门到精通⏪
 
🚚代码仓库:NEO的学习日记🚚
 
🌹关注我🫵带你学习C++
  🔝🔝

在这里插入图片描述

AVL树

  • 1. 前言
  • 2. AVL树的概念以及特性
  • 3. AVL树模拟实现基本框架
  • 4. AVL树插入函数深度剖析
  • 5. AVL树插入代码剖析(无旋转)
  • 6. AVL树的旋转操作深度剖析(一)
  • 7. AVL树的旋转操作深度剖析(二)
  • 8. AVL树旋转的代码实现
  • 9. 总结以及所有代码

1. 前言

如果你不知道什么是二叉搜索树
请一定先阅读这篇文章:

二叉搜索树深度剖析

二叉搜索树如果插入顺序是有序的
那么这棵树的查找效率将会是O(N)
所以说在实际情况下,二叉搜索很少被使用

为了解决二叉搜索树不稳定的问题
于是乎有人提出了AVL树结构,也就是
高度平衡二叉搜索树!

本章重点:

本篇文章着重讲解AVL树的概念以及
定义,并且在模拟实现AVL树前,将AVL
树的插入的情况做系统分析,最后模拟
实现AVL树的插入操作,进一步理解它!

2. AVL树的概念以及特性

AVL树通过一个特性来保证二叉
搜索的平衡性问题: 那就是任一
节点两边的子树高度差不超过1!

在这里插入图片描述
高度差一般是右子树高度减左子树高度

由于AVL树的这种特殊性质,使得它的
查找效率是百分百的O(logn),可以说
这是天才的发明,当插入或删除节点时,
高度差不符合要求后,可以通过旋转的
方式来重新让这棵树变成AVL树!

下面,我们一般尝试理解AVL树
一边来模拟实现它!

3. AVL树模拟实现基本框架

首先我们应该想到一点,当高度差
大一1时我们需要做处理,但是我们
怎么知道哪个节点高度差大于1呢?
因此应该在节点中多定义一个整数
来记录当前节点的左右高度差!

AVL树的节点结构体:

template<class K, class V>
struct AVLTreeNode   //高度平衡二叉搜索树
{AVLTreeNode(const pair<K,V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0){}//用三叉链,方便更新祖先的平衡因子AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;pair<K, V> _kv; //存储的数据int _bf; //balance factor平衡因子
};

有了节点的结构体后,定义一下
AVL树的基本结构吧:

template<class K,class V>
struct AVLTree
{typedef AVLTreeNode<K, V> Node;
private:Node* _root;//定义一个根节点
};

4. AVL树插入函数深度剖析

AVL数的插入有三个步骤:

  1. 按照二叉搜索树规则插入节点
  2. 插入完成后更新平衡因子
  3. 若平衡因子不正确需要采取措施

所以当前目标就是把这三步搞清楚

更新平衡因子规则:

  1. 新增在右,父亲的bf加一
    新增在左,父亲的bf减一

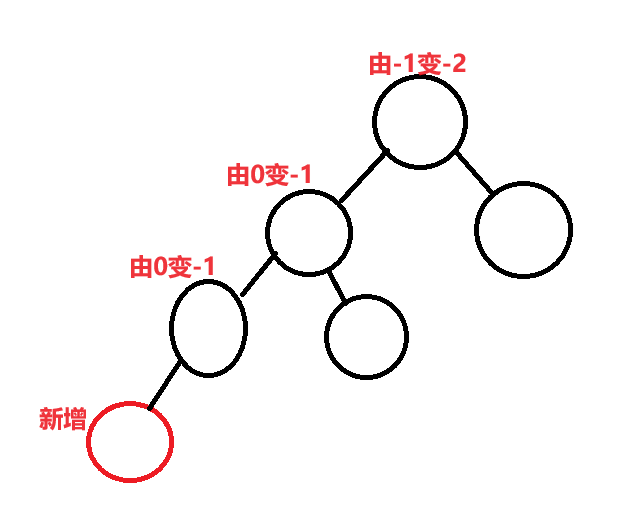
  2. 更新完成后,父亲的bf==1/-1,说明
    父亲插入前的bf一定是0,并且插入后
    一边高一边低,需要继续向上更新

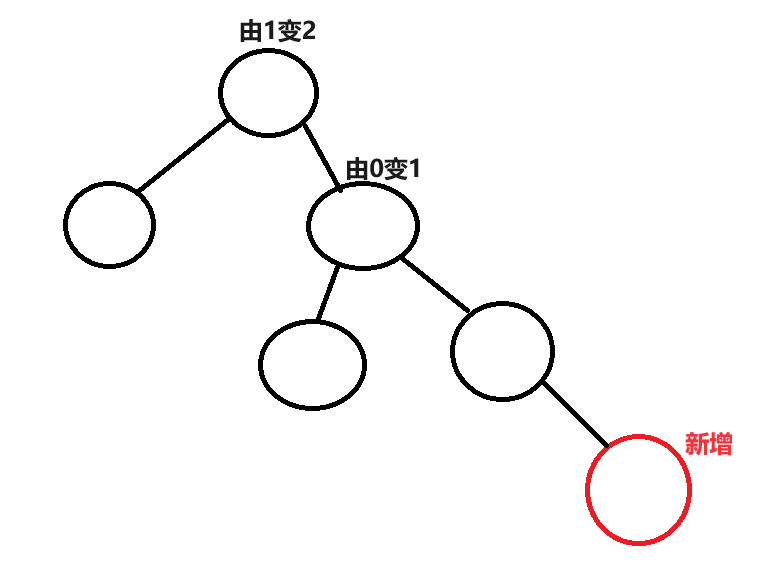
在这里插入图片描述

  1. 更新完成后,父亲的bf==0,说明父亲
    在插入前的bf是1/-1,并且插入后两边高度
    一致,就不需要继续往上更新了!

在这里插入图片描述

  1. 更新完成后,父亲的bf==2/-2,打破
    了平衡,父亲所在的子树要旋转处理

在这里插入图片描述

由于旋转处理的过程比较复杂
所以先将除了旋转的所有代码写出来
后再去讨论旋转的话题!

5. AVL树插入代码剖析(无旋转)

话不多说,直接上手!

bool insert(const pair<K, V>& kv)//第一步:按照二叉搜索树的方式插入值,第二步:调整平衡因子后旋转{if (_root == nullptr)//插入第一个节点时{_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur)//找到要插入节点的位置和它的父亲{if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else return false;}//走到这一步后,已经找到了位置,开空间后插入cur = new Node(kv);if (parent->_kv.first < kv.first)parent->_right = cur;elseparent->_left = cur;//此时new出来的节点的parent还指向空cur->_parent = parent;//插入完成后,此时需要查看平衡因子来控制平衡//沿着插入的位置往上更新平衡因子 while (parent)//由于parent需要不断向上更新,所以要使用循环!{if (cur == parent->_right)parent->_bf++;elseparent->_bf--;if (parent->_bf == 0)//不用向上更新了break;else if (parent->_bf == 1 || parent->_bf == -1)//若高度出现变化,需要往上更新{parent = parent->_parent;cur = cur->_parent;}else if (abs(parent->_bf) == 2)//说明parent所在的子树不平衡了,需要旋转处理{//后面再处理这个过程......}}
}

关于代码的解释都在注释中,请耐心查看!

6. AVL树的旋转操作深度剖析(一)

首先,旋转一共由四种情况,不管是
哪一种情况,我们的目的都是将原本
不平衡的树变成符合规则的AVL树!

先看两个最简单的例子:

左单选和右单旋:

在这里插入图片描述
在这里插入图片描述
大概了解了它的规则后,再来看泛型的:

  1. 右单旋
    在这里插入图片描述
  2. 左单旋:
    在这里插入图片描述

7. AVL树的旋转操作深度剖析(二)

当你了解了前两种最简单的情况后
就可以来看看"双旋"操作了!

还是先看看最简单的例子:

先左旋再右旋
先右旋再左旋

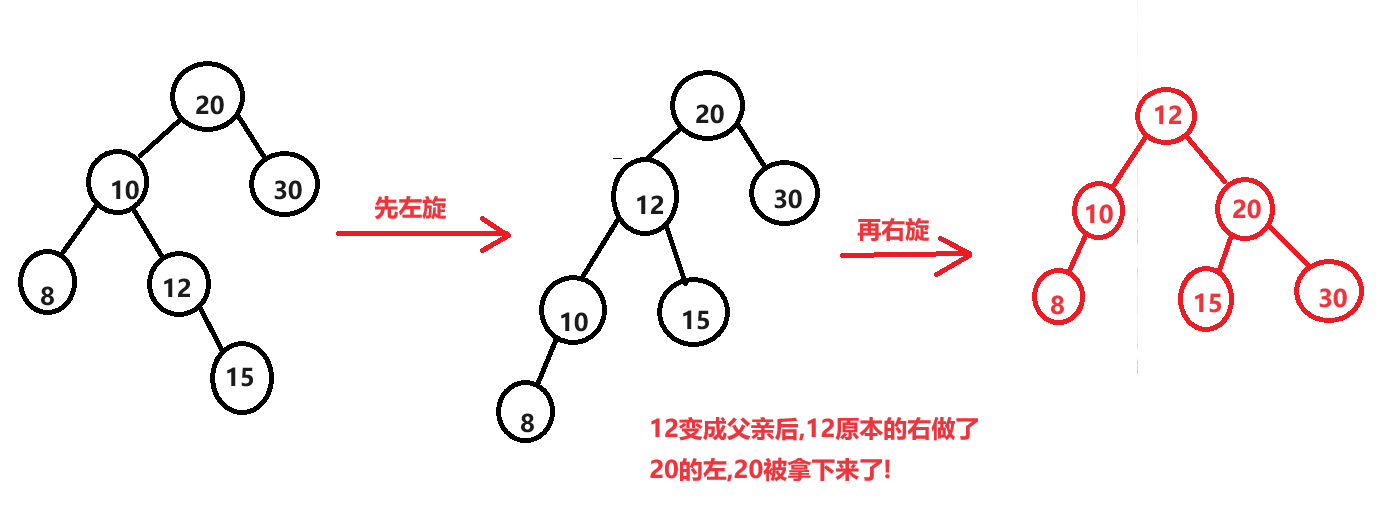
在这里插入图片描述

了解了最简单了例子后,直接上手!

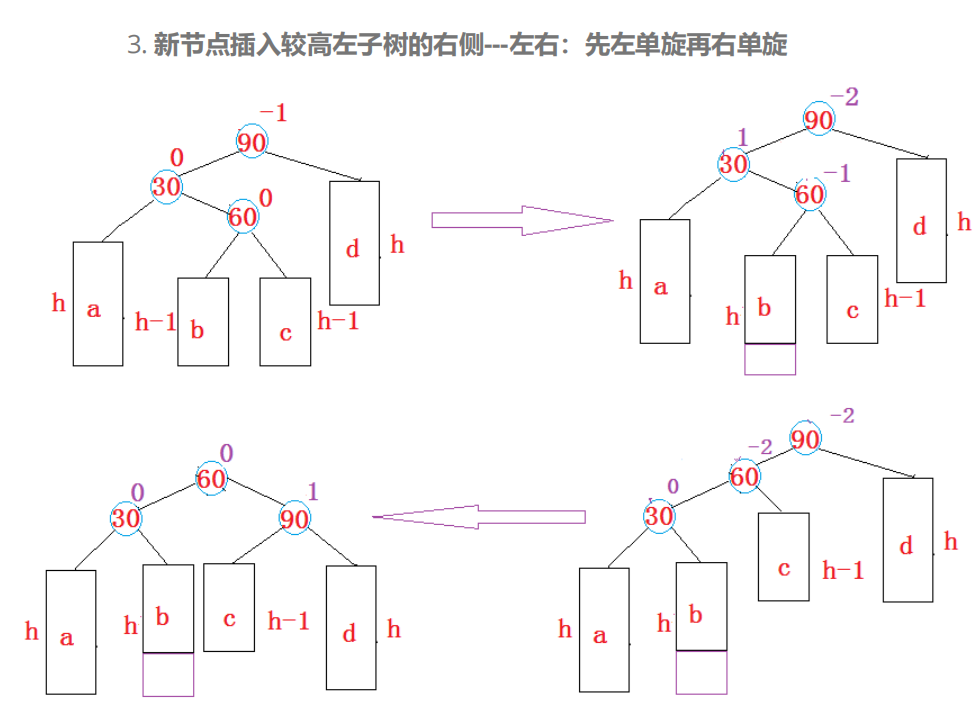
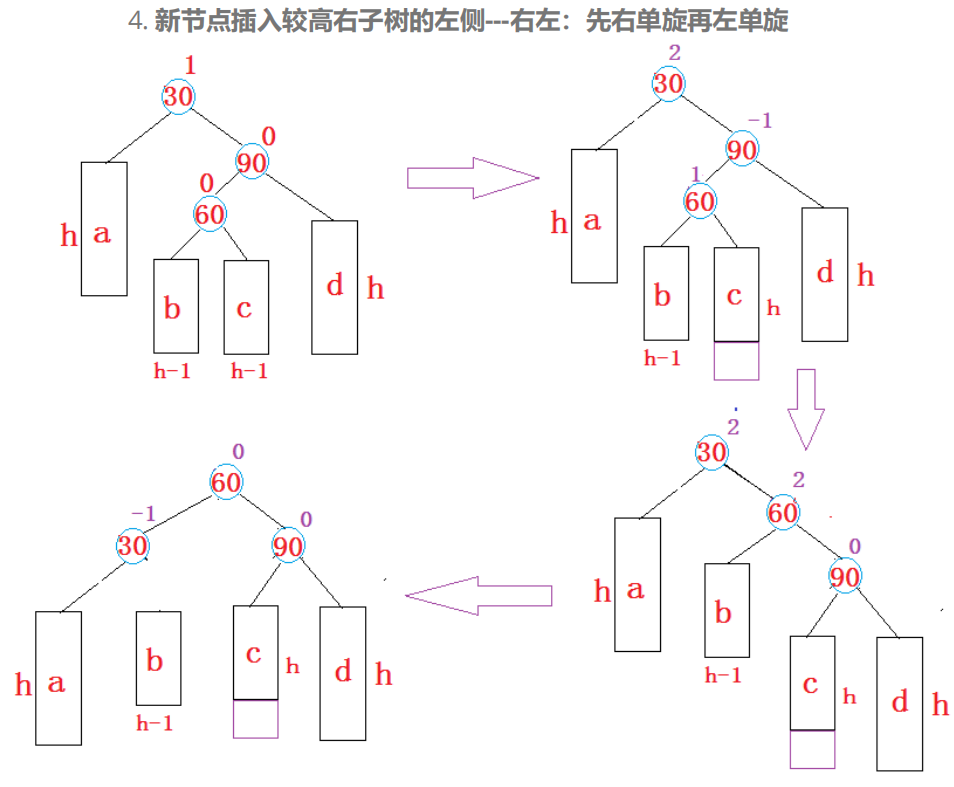
在这里插入图片描述

在这里插入图片描述

8. AVL树旋转的代码实现

void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (ppNode->_left == parent)ppNode->_left = subR;elseppNode->_right = subR;subR->_parent = ppNode;}subR->_bf = parent->_bf = 0;
}
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent)ppNode->_left = subL;elseppNode->_right = subL;subL->_parent = ppNode;}subL->_bf = parent->_bf = 0;
}
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);subLR->_bf = 0;if (bf == 1){parent->_bf = 0;subL->_bf = -1;}else if (bf == -1){parent->_bf = 1;subL->_bf = 0;}else if (bf == 0){parent->_bf = 0;subL->_bf = 0;}else assert(false);
}
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);subRL->_bf = 0;if (bf == 1){subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;parent->_bf = 0;}else if (bf == 0){parent->_bf = 0;subR->_bf = 0;}else assert(false);
}

你问我我怎么写出代码的?
那是一段痛苦的回忆,代码的验证就交给你们了
代码中对于平衡因子的更新有细节!

9. 总结以及所有代码

AVL树的模拟实现属于了解的内容
并不需要完全掌握,所以同学了只需
理解了AVL树的旋转即可,不要求手撕代码!
(当然前几年有学长面试时被要求手撕了doge)

AVL树模拟实现全部代码:

我的gitee仓库

🔎 下期预告:红黑树树深度剖析 🔍

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/214812.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

查企业联系电话的方法

查企业联系电话的方法

对于销售来说&#xff0c;获取准确、全面的企业联系方式&#xff0c;无疑是开发客户的基础与保障&#xff0c;因为任凭能力再高&#xff0c;说服能力多强&#xff0c;没有与客户接触的机会&#xff0c;这些都是无稽之谈。但是大家都知道&#xff0c;道理都懂&#xff0c;但是要…
阅读更多...
Java二级医院区域HIS信息管理系统源码（SaaS服务）

Java二级医院区域HIS信息管理系统源码（SaaS服务）

一个好的HIS系统&#xff0c;要具有开放性&#xff0c;便于扩展升级&#xff0c;增加新的功能模块&#xff0c;支撑好医院的业务的拓展&#xff0c;而且可以反过来给医院赋能&#xff0c;最终向更多的患者提供更好的服务。 系统采用前后端分离架构&#xff0c;前端由Angular、J…
阅读更多...
【MySQL】数据库基础操作

【MySQL】数据库基础操作

&#x1f451;专栏内容&#xff1a;MySQL⛪个人主页&#xff1a;子夜的星的主页&#x1f495;座右铭&#xff1a;前路未远&#xff0c;步履不停 目录 一、数据库操作1、创建数据库2、查看所有数据库3、选定指定数据库4、删除数据库 二、数据表操作1、创建数据表2、查看所有表3、…
阅读更多...
H5游戏和小程序游戏的区别是什么，分别有什么优势？

H5游戏和小程序游戏的区别是什么，分别有什么优势？

H5游戏和小程序游戏都是基于互联网的游戏形式&#xff0c;但它们在技术实现、发布平台和用户体验等方面存在一些区别。 技术实现&#xff1a; H5游戏&#xff1a; 使用HTML5、CSS3、JavaScript等Web技术进行开发。这意味着玩家可以通过任何支持Web浏览器的设备访问游戏&#…
阅读更多...
11-23 SSM4

11-23 SSM4

Ajax 同步请求 &#xff1a;全局刷新的方式 -> synchronous请求 客户端发一个请求&#xff0c;服务器响应之后你客户端才能继续后续操作&#xff0c;请求二响应完之后才能发送后续的请求&#xff0c;依次类推 有点&#xff1a;服务器负载较小&#xff0c;但是由于服务器相应…
阅读更多...
什么是网络安全工程师，你想知道的都在这里！

什么是网络安全工程师，你想知道的都在这里！

随着互联网的发展和大数据时代的到来&#xff0c;网络已经日渐深入到我们生活、工作中的方方面面&#xff0c;社会信息化和信息网络化&#xff0c;突破了应用信息在时间和空间上的障碍&#xff0c;使信息的价值不断提高。但是&#xff0c;与此同时&#xff0c;网页篡改、计算机…
阅读更多...
3D卷积的理解

3D卷积的理解

卷积核不仅需要在高宽这两个维度上进行滑动&#xff0c;还需要在时间维度上进行滑动
阅读更多...
模拟退火算法应用——求解函数的最小值

模拟退火算法应用——求解函数的最小值

仅作自己学习使用 一、问题 需求&#xff1a; 计算函数 的极小值&#xff0c;其中个体x的维数n10&#xff0c;即x(x1,x2,…,x10)&#xff0c;其中每一个分量xi均需在[-20,20]内。因此可以知道&#xff0c;这个函数只有一个极小值点x (0,0,…,0)&#xff0c;且其极小值是0&…
阅读更多...
PHP预约上门回收废品系统的代码披露

PHP预约上门回收废品系统的代码披露

PHP预约上门回收废品系统的代码披露 <?phpnamespace app\admin\controller;class Code {public function getTopDomainhuo(){error_reporting(0);$host $_SERVER["HTTP_HOST"];$matchstr "[^\\.]\\.(?:(" . $host . ")|\\w{2}|((" . $ho…
阅读更多...
node-red - 节点实战总结1

node-red - 节点实战总结1

node-red - 节点实战总结1 二、功能2.1 循环(for\while) 三、网络四、序列五、解析六、存储七、协议7.1 modbus协议7.2 opcua 八、formats8.1 时间格式化与时区转换 二、功能 2.1 循环(for\while) 安装节点node-red-contrib-loop-processing,该节点支持三种方式的循环&#xf…
阅读更多...
classifier-free-guidance 扩散模型引导生成

classifier-free-guidance 扩散模型引导生成

浅谈扩散模型的有分类器引导和无分类器引导 - 知乎这篇文章主要比较一下扩散模型的引导生成的三种做法的区别。它们分别是用显式分类器引导生成的做法&#xff0c;用隐式无分类器引导的做法和用CLIP计算跨模态间的损失来引导生成的做法。 Classifier-Guidance: Diffusion Mode……
阅读更多...
虽不想承认，但这就是CSGO游戏搬砖行业的现状

虽不想承认，但这就是CSGO游戏搬砖行业的现状

CSGO搬砖日常出货更新 其实整个搬砖市场&#xff0c;现在已经变得乌烟瘴气&#xff0c;散发着“恶臭”。我个人非常鄙视那些虚有其表&#xff0c;大小通吃的做法&#xff0c;那些甚至连搬砖数据都看不懂的人&#xff0c;也出来吹嘘着“实力强大&#xff0c;经验丰富”。这个世界…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023