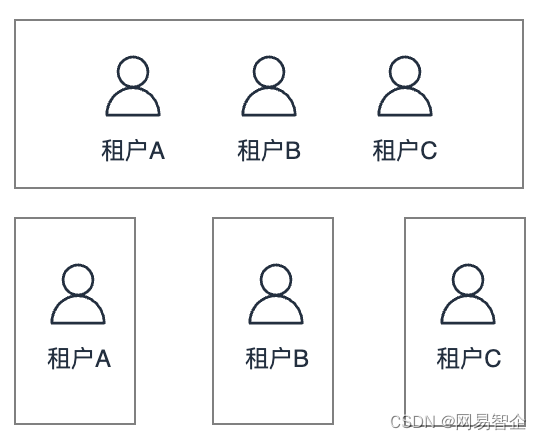
求导算子:,相当于
二阶线性微分算子
符号:
性质:设函数y=y(x),,
,二阶可导,C、C1,C2为常数,则有
叠加原理
设函数 ,
都是L[y]的解,
C1,C2是常数,则c1y1+c2y2,也是L[y]的解
函数线性相关和线性无关的定义
二阶非齐次线性微分方程通解的结构定理
定理:
设是
的一个特解。
是
的通解,则
也是
的通解,其中C1/C2是任意常数。
广义叠加原理
设、
分别是
、
的解,
则是
的解。
定理五
设是
的解,则
、
分别是
,
的解