0. 前言

整个初始化部分的pipeline如下所示，参照之前的博客，接下来根据代码一步步讲解。

1. 旋转约束标定旋转外参Rbc

上回讲了processImage中addFeatureCheckParallax完成了对KF的筛选，我们知道了2nd是否为KF，接下来是初始化和后端求解部分。对于初始化，先标定Ric外参：

//不知道关于外参的任何info，需要标定
if(ESTIMATE_EXTRINSIC == 2)
{ROS_INFO("calibrating extrinsic param, rotation movement is needed");if (frame_count != 0){// 找相邻两帧(bk, bk+1)之间的tracking上的点，构建一个pair，所有pair是一个vector，即corres(pondents),// 要求it.start_frame <= frame_count_l && it.endFrame() >= frame_count_rvector<pair<Vector3d, Vector3d>> corres = f_manager.getCorresponding(frame_count - 1, frame_count);Matrix3d calib_ric;//旋转约束+SVD分解求取Ric旋转外参if (initial_ex_rotation.CalibrationExRotation(corres, pre_integrations[frame_count]->delta_q, calib_ric)){ROS_WARN("initial extrinsic rotation calib success");ROS_WARN_STREAM("initial extrinsic rotation: " << endl << calib_ric);ric[0] = calib_ric;RIC[0] = calib_ric;ESTIMATE_EXTRINSIC = 1;}}
}

CalibrationExRotation是主要函数，用于标定旋转外参Ric，理论依据是旋转约束（下面会讲）。

下面依次讲解各部分代码。

1.1 SfM求取relative pose

重点函数solveRelativeR。
其中八点法求取Rt，correspondents不小于9时，1.求取E，2.反解并test出4组Rt，3.使用三角化出的深度来判断正确的那组Rt，这里 求E(看14讲)，由E反解出4组Rt(看之前SLAM博客)，三角化(看VIO博客)，带点进Rt判断正深度来确定正确的Rt(看代码注释) 基本上都是调用的cv库函数，原理之前的SLAM和VIO课程中都有学过，相应回顾即可。

Matrix3d InitialEXRotation::solveRelativeR(const vector<pair<Vector3d, Vector3d>> &corres)
{//大于9个点才进行求解，否则直接返回Identityif (corres.size() >= 9){vector<cv::Point2f> ll, rr;for (int i = 0; i < int(corres.size()); i++){//将找到的这两帧间的所有corr点收集起来，用于后面的 对极约束求本质矩阵E 和 三角化求深度ll.push_back(cv::Point2f(corres[i].first(0), corres[i].first(1)));rr.push_back(cv::Point2f(corres[i].second(0), corres[i].second(1)));}cv::Mat E = cv::findFundamentalMat(ll, rr);//对极约束求本质矩阵E=t^Rcv::Mat_<double> R1, R2, t1, t2;decomposeE(E, R1, R2, t1, t2);//这应该是什么判断if (determinant(R1) + 1.0 < 1e-09){E = -E;decomposeE(E, R1, R2, t1, t2);}//用四个解分别进行Triangulation，带入points，求深度为正的比例，取比例最大的作为正确的Rt解double ratio1 = max(testTriangulation(ll, rr, R1, t1), testTriangulation(ll, rr, R1, t2));double ratio2 = max(testTriangulation(ll, rr, R2, t1), testTriangulation(ll, rr, R2, t2));cv::Mat_<double> ans_R_cv = ratio1 > ratio2 ? R1 : R2;Matrix3d ans_R_eigen;for (int i = 0; i < 3; i++)for (int j = 0; j < 3; j++)ans_R_eigen(j, i) = ans_R_cv(i, j);return ans_R_eigen;}return Matrix3d::Identity();
}

三角化以及反解E

//将一个点
double InitialEXRotation::testTriangulation(const vector<cv::Point2f> &l,const vector<cv::Point2f> &r,cv::Mat_<double> R, cv::Mat_<double> t)
{cv::Mat pointcloud;//因为triangulatePoints函数要传入分别两帧的pose，所以通常假设第一帧的外参pose是Identity，这样由relative Rt即可得第二帧的pose，即P1 = relative Rtcv::Matx34f P = cv::Matx34f(1, 0, 0, 0,0, 1, 0, 0,0, 0, 1, 0);cv::Matx34f P1 = cv::Matx34f(R(0, 0), R(0, 1), R(0, 2), t(0),R(1, 0), R(1, 1), R(1, 2), t(1),R(2, 0), R(2, 1), R(2, 2), t(2));//pointcloud是三角化的结果，是(4*m)维，其中m是传入的correspondents的对数，pointcloud每一列都是相应的三角化之后的为归一化的齐次坐标cv::triangulatePoints(P, P1, l, r, pointcloud);int front_count = 0;for (int i = 0; i < pointcloud.cols; i++){//用于归一化，使最后一维为1，这样前三维就是world系下的3D点了，乘以相应的pose就能转化为每个camera系下的3D点(非归一化平面，// 如果再 /p_3d_r(2) 则可转化为归一化平面下的3D点，但是要使用深度是否>0来筛选出正确的Rt的解，所以就不归一化，见《14讲》P169)double normal_factor = pointcloud.col(i).at<float>(3);cv::Mat_<double> p_3d_l = cv::Mat(P) * (pointcloud.col(i) / normal_factor);cv::Mat_<double> p_3d_r = cv::Mat(P1) * (pointcloud.col(i) / normal_factor);if (p_3d_l(2) > 0 && p_3d_r(2) > 0)front_count++;//统计正深度点的个数}ROS_DEBUG("MotionEstimator: %f", 1.0 * front_count / pointcloud.cols);return 1.0 * front_count / pointcloud.cols;//统计所有pointcloud中正深度点的比率（不是很明白，不应该都是正的吗？直接取ratio=1的不行吗？）
}//从E中分解出Rt
void InitialEXRotation::decomposeE(cv::Mat E,cv::Mat_<double> &R1, cv::Mat_<double> &R2,cv::Mat_<double> &t1, cv::Mat_<double> &t2)
{cv::SVD svd(E, cv::SVD::MODIFY_A);//绕z顺时针90°cv::Matx33d W(0, -1, 0,1, 0, 0,0, 0, 1);//绕z逆时针90°cv::Matx33d Wt(0, 1, 0,-1, 0, 0,0, 0, 1);R1 = svd.u * cv::Mat(W) * svd.vt;R2 = svd.u * cv::Mat(Wt) * svd.vt;t1 = svd.u.col(2);//3*3取最后一个是待求量（TODO:为什么t2可以直接取负号？）t2 = -svd.u.col(2);
}

1.2 旋转约束和旋转residual的构建

两个路径求取的$q_{b_k{c}_{k+1}}$理想状态下相等，详见VIO Ch7博客2.2节
$$\begin{array}{r}{q}_{b_k{c}_{k+1}}=q_{b_k{b}_{k+1}}\ast q_{bc}=q_{bc}\ast q_{c_k{c}_{k+1}}\end{array}$$
但是实际情况，二者之间存在误差，即为residual，移项(左移右)即得residual：
$$\begin{array}{rl}residual& =q_{bc}^{-1}\ast q_{b_k{b}_{k+1}}^{-1}\ast q_{bc}\ast q_{c_k{c}_{k+1}}\\ & =q_{cb}\ast q_{b_{k+1}{b}_k}\ast q_{cb}^{-1}\ast q_{c_k{c}_{k+1}}\end{array}\text{\hspace{1em}(1.1)(1.2)}$$
上式(1.1)和(1.2)两种形式分别对应旋转外参$q_{bc}$和$q_{cb}$，跟后面左右乘的定义方式有关，代码中使用的(1.2)形式的定义，左乘L定义为 相机旋转四元数的左乘矩阵，右乘R定义为 IMU旋转四元数的右乘矩阵，下面会讲。

对应到CalibrationExRotation代码中：
Rc即$q_{c_k{c}_{k+1}}$，由SfM获得，从第$k+1$帧到第$k$帧的rotation
Rimu即delta_q即$q_{b_{k+1}{b}_k}$：由IMU预积分获得，从第$k$帧积分到第$k+1$帧
所以式(1.2)中剩下的左边部分$q_{cb}\ast q_{b_{k+1}{b}_k}\ast q_{cb}^{-1}$对应代码中的Rc_g

1.3 左乘右乘的构建

由于使用了式(1.2)形式来构建左右乘，所以式(1.2)整理为
$$\begin{array}{r}([{\mathbf{q}}_{c_k{c}_{k+1}}{]}_{\mathbf{L}}-[q_{b_{k+1}{b}_k}{]}_{\mathbf{R}}){\mathbf{q}}_{bc}=0\end{array}$$

崔华坤PDF中的

---

文献中的

二者形式上有差别，但是本质上应该是相同的，崔华坤PDF中的应该是根据代码推出来的，我们暂且使用这一套，对应到代码中：

//L为相机旋转四元数的左乘矩阵，记四元数为(w,x,y,z)
//实际构建的是qc_b
//构建结果为
//w -z  y  x
//z  w -x  y
//-y x  w  z
//-z -y -z  w
double w = Quaterniond(Rc[i]).w();
Vector3d q = Quaterniond(Rc[i]).vec();
L.block<3, 3>(0, 0) = w * Matrix3d::Identity() + Utility::skewSymmetric(q);//构建A左上角3*3
L.block<3, 1>(0, 3) = q;
L.block<1, 3>(3, 0) = -q.transpose();
L(3, 3) = w;//R为IMU旋转四元数的右乘矩阵，同样记四元数为(w,x,y,z)
//构建结果为
//w  z  -y  x
//-z  w  x  y
//y  -x  w  z
//-x -y -z  w
Quaterniond R_ij(Rimu[i]);
w = R_ij.w();
q = R_ij.vec();
R.block<3, 3>(0, 0) = w * Matrix3d::Identity() - Utility::skewSymmetric(q);
R.block<3, 1>(0, 3) = q;
R.block<1, 3>(3, 0) = -q.transpose();
R(3, 3) = w;

1.4 系数矩阵A的构建

如上构建出来的四元数左右乘矩阵均为(4*4)维，每组可构建一个式(2)所示的方程，多组correspondents构成多个方程，组成超定方程组，于是就需要构建超定方程组的系数矩阵$A$，维度为(frame_count * 4, 4)，如下所示：

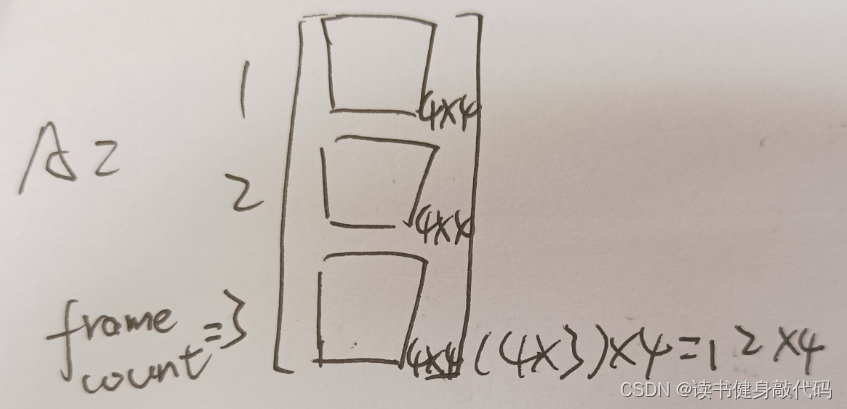
使用 SVD分解求解超定方程组，取最后一个特征值对应的特征向量即为我们所求的${\mathbf{q}}_{cb}$

1.5 鲁棒核函数

为了使方程具有更好的数值稳定性，在构建系数矩阵$A$时根据每项的residual为相应的(4*4)块添加了权重$\omega$，权重由Huber损失函数计算而得：

对应代码：

Quaterniond r1(Rc[i]);
Quaterniond r2(Rc_g[i]);// 这里的angular_distance是角度误差，5是Huber核函数中的threshold，
// angularDistance: returns the angle (in radian) between two rotations返回两个旋转之间的相对旋转(弧度表示)，再换算为角度
// 旋转矩阵R和轴角theta之间的关系：tr(R)=1+2cos(theta)，所以theta=arccos( (tr(R)-1)/2 )，就是angularDistance的返回值
double angular_distance = 180 / M_PI * r1.angularDistance(r2);
ROS_DEBUG("%d %f", i, angular_distance);//Huber鲁棒核函数
double huber = angular_distance > 5.0 ? 5.0 / angular_distance : 1.0;

其中angularDistance函数应该对应着上图的式(9)，输出rad，代码中又转化为angle。式(8)中的threshold设为5。如此，方程的构建部分就全部完成。

1.6 $q_{cb}$ 的求解

使用SVD分解求解超定方程组，根据之前Triangulation的经验(博客第3.2节)，需要对特征值${\sigma }_4/{\sigma }_3$的比值进行判断，但是此处发现并没有满足远小于的条件，后面再探究吧。

关于特征值的判断条件：

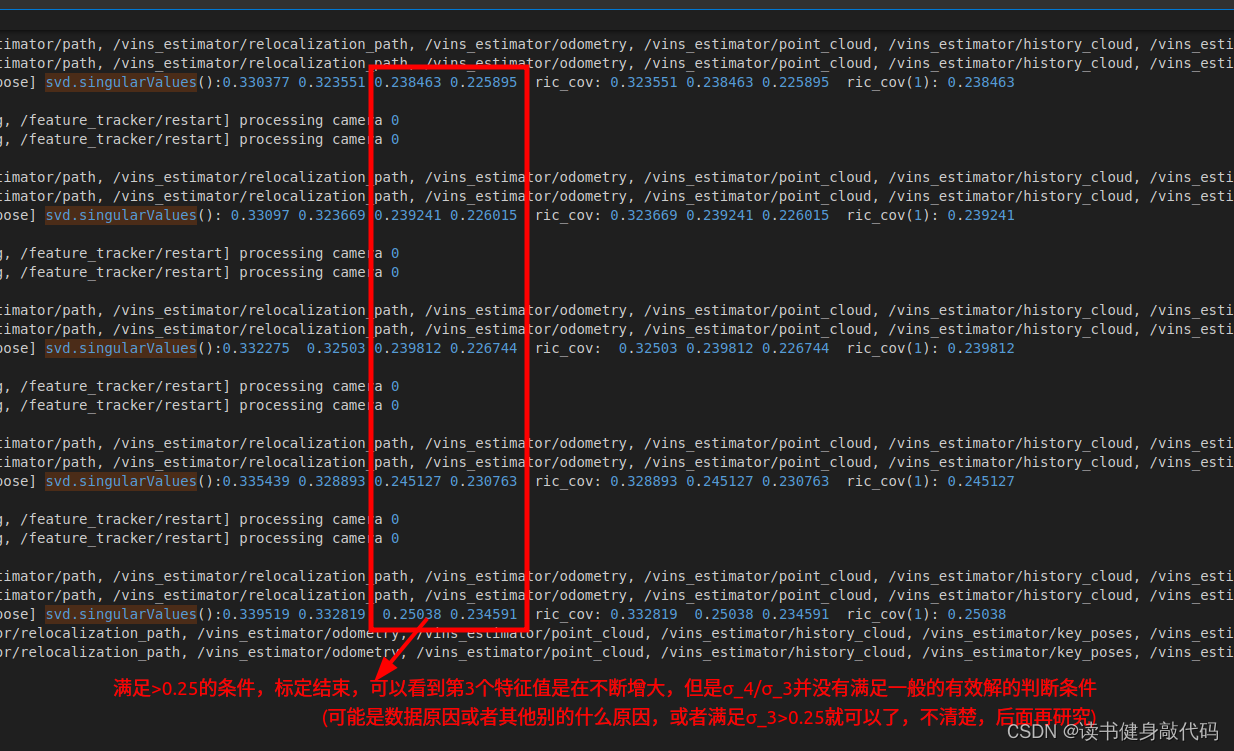
至此已完成旋转外参标定的所有理论和代码部分的对应，附上该部分完整代码注释。

// 旋转约束标定Ric，两条路径求取的旋转应相同，所以移项构建方程，并根据误差项r的鲁棒核函数值w(r)对每一项的系数进行加权，将大于threshold的部分的权值设的较小，
// 最终使用SVD分解求取特征值最小的特征向量
// 详见第7章博客：https://blog.csdn.net/qq_37746927/article/details/133782580#t4
// 旋转约束：qbk_ck+1=qbk_bk+1*qbc=qbc*qck_ck+1
bool InitialEXRotation::CalibrationExRotation(vector<pair<Vector3d, Vector3d>> corres, Quaterniond delta_q_imu, Matrix3d &calib_ric_result)
{frame_count++;//correspondents对数不小于9时求出Rt: 1.求取E，2.反解并test出4组Rt，3.使用三角化出的深度来判断正确的那组Rt//Rc即Rck_ck+1Rc.push_back(solveRelativeR(corres));//Rimu即delta_q即qbk_bk+1即Rbk+1_bkRimu.push_back(delta_q_imu.toRotationMatrix());//旋转约束：qbk_ck+1 = qbk_bk+1 * qbc = qbc * qck_ck+1,移项(左移右)即得residual=qbc^(-1)*qbk_bk+1^(-1) * qbc * qck_ck+1，//其中Rc=qck_ck+1，剩下的项就是qbc^(-1) * qbk_bk+1^(-1) * qbc = qcb * qbk_bk+1^(-1) * qcb^(-1)，记为Rc_g//上式左边是rbc版本构建A时L为IMU，右边是rcb版本，构建A时L为camera，这里采用了后者rcb，L为cameraRc_g.push_back(ric.inverse() * delta_q_imu * ric);//Rc_g * Rc就是整个左移右的residual//构建A矩阵Eigen::MatrixXd A(frame_count * 4, 4);//这个维度是什么意思？从第[1]帧开始A.setZero();int sum_ok = 0;for (int i = 1; i <= frame_count; i++){Quaterniond r1(Rc[i]);Quaterniond r2(Rc_g[i]);// 这里的angular_distance是角度误差，5是Huber核函数中的threshold，// angularDistance: returns the angle (in radian) between two rotations返回两个旋转之间的相对旋转(弧度表示)，再换算为角度// 旋转矩阵R和轴角theta之间的关系：tr(R)=1+2cos(theta)，所以theta=arccos( (tr(R)-1)/2 )，就是angularDistance的返回值double angular_distance = 180 / M_PI * r1.angularDistance(r2);ROS_DEBUG("%d %f", i, angular_distance);//Huber鲁棒核函数double huber = angular_distance > 5.0 ? 5.0 / angular_distance : 1.0;++sum_ok;Matrix4d L, R;//L为相机旋转四元数的左乘矩阵，记四元数为(w,x,y,z)//实际构建的是qc_b//构建结果为//w -z  y  x//z  w -x  y//-y x  w  z//-z -y -z  wdouble w = Quaterniond(Rc[i]).w();Vector3d q = Quaterniond(Rc[i]).vec();L.block<3, 3>(0, 0) = w * Matrix3d::Identity() + Utility::skewSymmetric(q);//构建A左上角3*3L.block<3, 1>(0, 3) = q;L.block<1, 3>(3, 0) = -q.transpose();L(3, 3) = w;//R为IMU旋转四元数的右乘矩阵，同样记四元数为(w,x,y,z)//构建结果为//w  z  -y  x//-z  w  x  y//y  -x  w  z//-x -y -z  wQuaterniond R_ij(Rimu[i]);w = R_ij.w();q = R_ij.vec();R.block<3, 3>(0, 0) = w * Matrix3d::Identity() - Utility::skewSymmetric(q);R.block<3, 1>(0, 3) = q;R.block<1, 3>(3, 0) = -q.transpose();R(3, 3) = w;A.block<4, 4>((i - 1) * 4, 0) = huber * (L - R);}JacobiSVD<MatrixXd> svd(A, ComputeFullU | ComputeFullV);Matrix<double, 4, 1> x = svd.matrixV().col(3);Quaterniond estimated_R(x);ric = estimated_R.toRotationMatrix().inverse();//这里可以看到求得ric实际上是rci=rcb//cout << svd.singularValues().transpose() << endl;//cout << ric << endl;Vector3d ric_cov;ric_cov = svd.singularValues().tail<3>();ROS_DEBUG_STREAM("svd.singularValues():" << svd.singularValues().transpose() << "  ric_cov: " << ric_cov.transpose() << "  ric_cov(1): " << ric_cov(1));//这个取ric_cov相当于取所有特征值里面的第三个，要求它大于某个阈值，最后一个理论上来说应该是特别小的，//根据SVD有效性判断方法，σ4 << σ3才算解有效，σ4/σ3比值的阈值一般取1e-2~1e-4算远小于，//但是实际Debug发现SVD解出来的一半也不满足这个条件，所以ESTIMATE_EXTRINSIC直接config为0，不标了？if (frame_count >= WINDOW_SIZE && ric_cov(1) > 0.25){calib_ric_result = ric;return true;}elsereturn false;
}

2. 旋转约束标定gyro bias