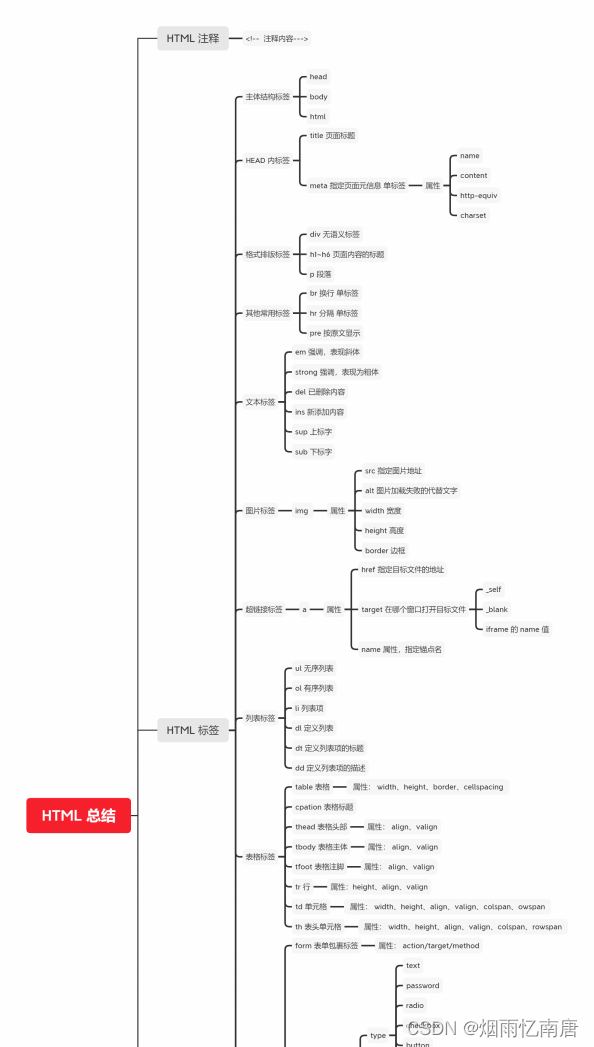
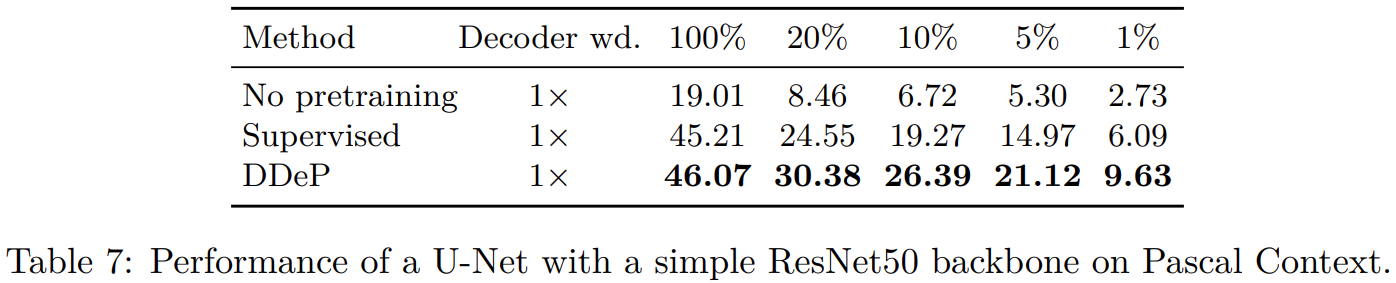
我们知道矩阵是一个非常强大的数据结构，在动态规划以及各种图论算法上都有广泛的应用，当然矩阵有着不足的地方就是空间和时间复杂度都维持在 N2 上，比如 1w 个数字建立一个矩阵，在内存中会占用 1w*1w=1 亿的类型空间，这时就会遇到 outofmemory。。。那么面临的一个问题就是如何来压缩矩阵，当然压缩的方式有很多种，这里就介绍一个顺序表的压缩方式：三元组。

一、三元组

有时候我们的矩阵中只有零星的一些非零元素，其余的都是零元素，那么我们称之为稀疏矩阵，当然没有绝对的说有多少个零元素才算稀疏。

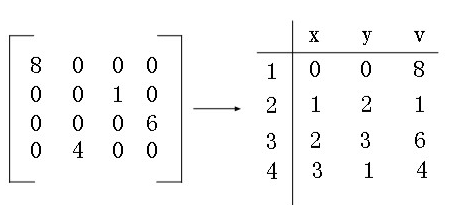
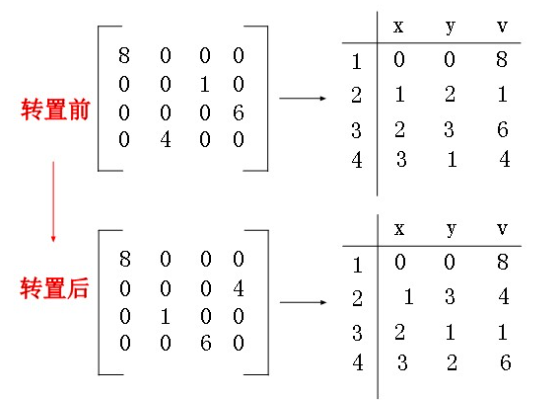
针对上面的这个无规律的存放非零元素，三元组提出了一种方法，就是仅仅记录矩阵中的非零元素以及它的行，列以及值 N(x,y,v)构成的一个三元组，标识一个稀疏矩阵的话，还要记录该矩阵的阶数，这样我们就将一个二维的变成了一个一维，极大的压缩的存储空间，这里要注意的就是，三元组的构建采用“行“是从上到下，“列”也是从左到右的方式构建的顺序表。

 /// <summary>/// 三元组/// </summary>public class Unit{public int x;public int y;public int element;}/// <summary>/// 标识矩阵/// </summary>public class SPNode{//矩阵总行数public int rows;//矩阵总列数public int cols;//非零元素的个数public int count;//矩阵中非零元素public List<Unit> nodes = new List<Unit>();}

其实说到这里也就差不多了，我们只要知道三元组是用来做矩阵压缩的一个顺序存储方式即可，然后知道怎么用三元组表来做一些常规的矩阵运算，好了，既然说已经做成线性存储了，那就做个“行列置换”玩玩。

二、行列置换

做行列置换很容易，也就是交换"非零元素"的(x,y)坐标，要注意的就是，原先我们的三元组采用的是”行优先“，所以在做转置的时候需要遵循"列优先“。

 /// <summary>/// 行转列运算/// </summary>/// <param name="spNode"></param>/// <returns></returns>public SPNode ConvertSpNode(SPNode spNode){//矩阵元素的x和y坐标进行交换SPNode spNodeLast = new SPNode();//行列互换spNodeLast.rows = spNode.cols;spNodeLast.cols = spNode.rows;spNodeLast.count = spNode.count;//循环原矩阵的列数 (行列转换)for (int col = 0; col < spNode.cols; col++){//循环三元组行的个数for (int sp = 0; sp < spNode.count; sp++){var single = spNode.nodes[sp];//找到三元组中存在的相同编号if (col == single.y){spNodeLast.nodes.Add(new Unit(){x = single.y,y = single.x,element = single.element});}}}return spNodeLast;}

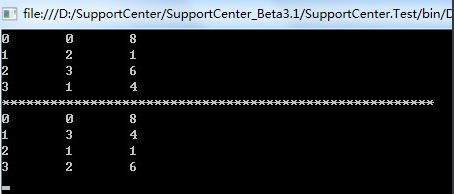
最后是总的代码:

 using System;using System.Collections.Generic;using System.Linq;using System.Text;using System.Diagnostics;using System.Threading;using System.IO;namespace ConsoleApplication2{public class Program{public static void Main(){Martix martix = new Martix();//构建三元组var node = martix.Build();foreach (var item in node.nodes){Console.WriteLine(item.x + "\t" + item.y + "\t" + item.element);}Console.WriteLine("******************************************************");var mynode = martix.ConvertSpNode(node);foreach (var item in mynode.nodes){Console.WriteLine(item.x + "\t" + item.y + "\t" + item.element);}Console.Read();}}public class Martix{/// <summary>/// 三元组/// </summary>public class Unit{public int x;public int y;public int element;}/// <summary>/// 标识矩阵/// </summary>public class SPNode{//矩阵总行数public int rows;//矩阵总列数public int cols;//非零元素的个数public int count;//矩阵中非零元素public List<Unit> nodes = new List<Unit>();}/// <summary>/// 构建一个三元组/// </summary>/// <returns></returns>public SPNode Build(){SPNode spNode = new SPNode();//遵循行优先的原则spNode.nodes.Add(new Unit() { x = 0, y = 0, element = 8 });spNode.nodes.Add(new Unit() { x = 1, y = 2, element = 1 });spNode.nodes.Add(new Unit() { x = 2, y = 3, element = 6 });spNode.nodes.Add(new Unit() { x = 3, y = 1, element = 4 });//4阶矩阵spNode.rows = spNode.cols = 4;//非零元素的个数spNode.count = spNode.nodes.Count;return spNode;}/// <summary>/// 行转列运算/// </summary>/// <param name="spNode"></param>/// <returns></returns>public SPNode ConvertSpNode(SPNode spNode){//矩阵元素的x和y坐标进行交换SPNode spNodeLast = new SPNode();//行列互换spNodeLast.rows = spNode.cols;spNodeLast.cols = spNode.rows;spNodeLast.count = spNode.count;//循环原矩阵的列数 (行列转换)for (int col = 0; col < spNode.cols; col++){//循环三元组行的个数for (int sp = 0; sp < spNode.count; sp++){var single = spNode.nodes[sp];//找到三元组中存在的相同编号if (col == single.y){spNodeLast.nodes.Add(new Unit(){x = single.y,y = single.x,element = single.element});}}}return spNodeLast;}}}