线段树

前言

对于求数组区间和我们可以处理出前缀和后可以在O(1)的时间内计算出任意区间和，但是前缀和的缺点在于一旦区间发生改变我们就要重新计算前缀和，当频繁进行区间操作时前缀和的优势荡然无存，所以我们需要一种数据结构来解决这类需求。

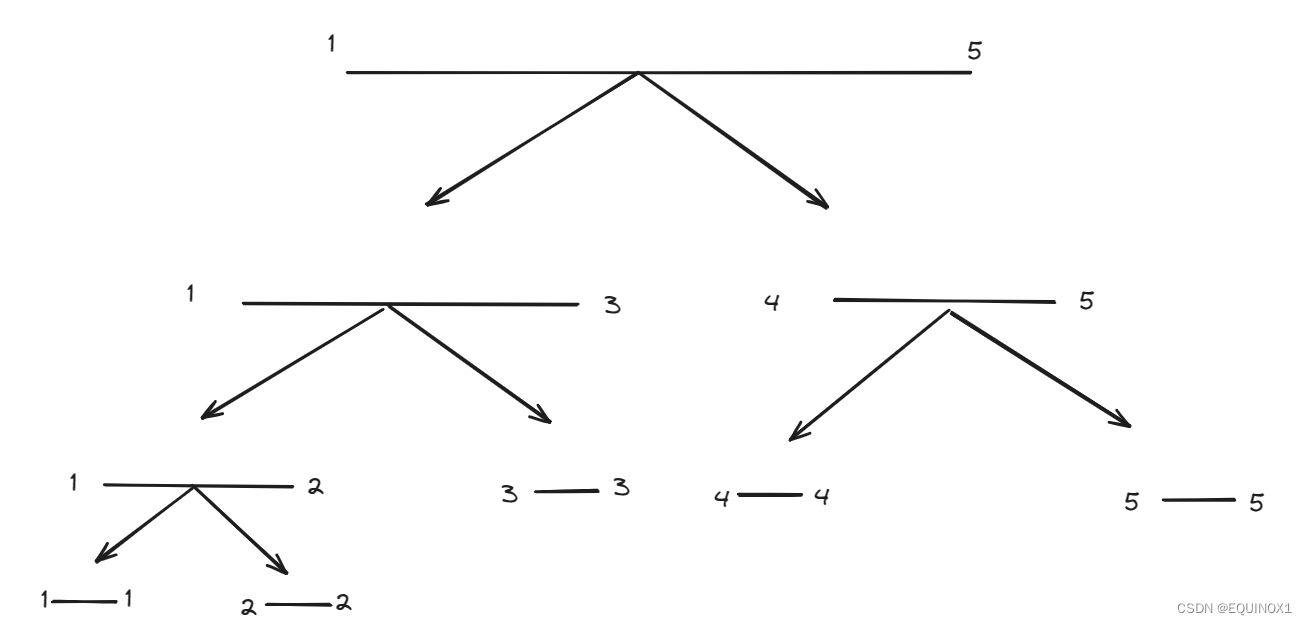
**线段树(segment tree)**是分治思想在线性数据上的一种应用，通过把一段区间不断分治为小区间来进行建树。

我们把一段区间不断向下二分，会发现整体的结构形似一棵二叉树。

一、线段树的定义

线段树是基于分治思想的二叉树，用来维护区间信息（区间信息，区间最值，区间gcd等），可以在logn的时间内执行区间修改和区间查询。

线段树中每个叶子节点存储元素本身，非叶子节点存储区间内元素的统计值。

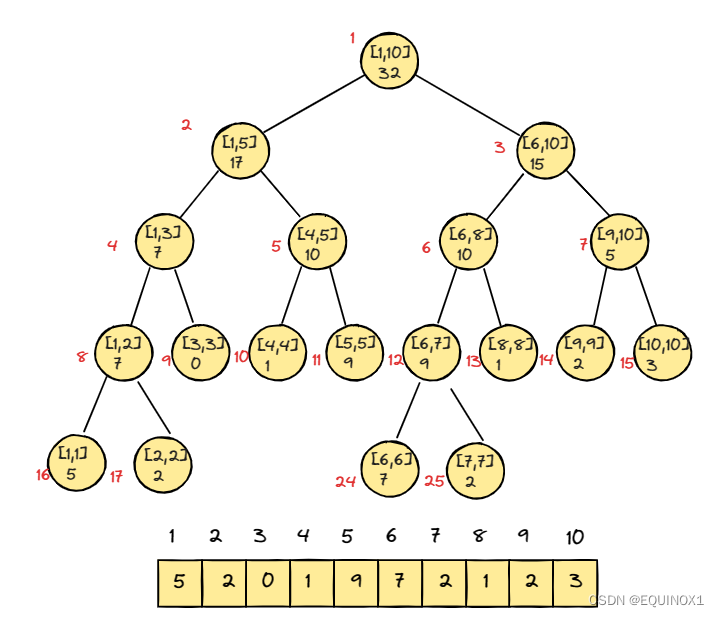
上图就是一棵线段树。

二、线段树的结构与建立

这里选择静态建立

2…1 节点定义

//#define lc p << 1
//#define rc p << 1 | 1
//constexpr int N = 5e5 + 10;
//int n, a[N];
struct Node
{int l, r, sum;
} tree[N * 4];//为什么开N*4后面有证明

2.2 递归建树

建树的过程其实就是对一段数组不断往下分治的过程。

建树过程如下：

1. l，r代表当前节点的区间，p代表节点下标索引
2. 如果l == r，说明是叶子节点，建立完就return
3. 否则，将区间[l , r]二分为[l , mid] , [mid + 1 , r]分别建立左右子树
4. 更新当前节点的sum值

void build(int p, int l, int r)
{tree[p] = {l, r, a[l]};if (l == r)return;int m = (l + r) >> 1;build(lc, l, m);build(rc, m + 1, r);tree[p].sum = tree[lc].sum + tree[rc].sum;
}

2.3 静态数组空间的解释

我们为什么开辟4*N个节点呢？

先来看最简单的情况，我们的线段树恰好为一棵满二叉树，那么我们最后一层叶子节点个数即为数组长度n，它的上面所有节点的数目为n - 1，那么最大编号为(n - 1) * 2 + 1

否则，由于每次划分出的两个区间长度最多差1，我们的线段树的非满二叉树情况只可能是一棵满二叉树的若干叶子节点上分出若干二叉

也就是说我们此时n = 2 ^ m + 2 * k(k = 1 , 2 , 3…)

如下图为例，n = 2 ^ m + 2

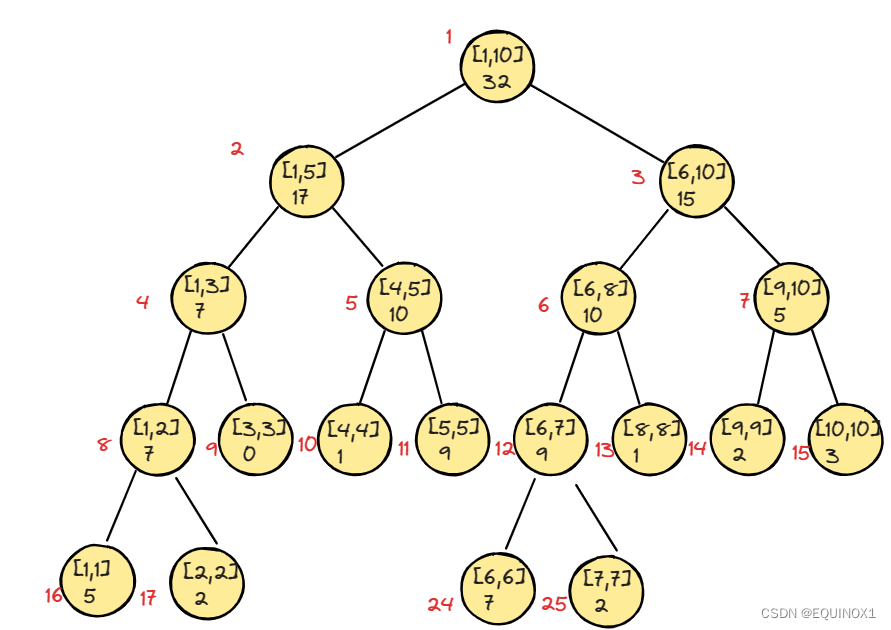
对于非满二叉树的情况，就是在一棵满二叉树的叶子节点层增加若干二叉的情况，我们发现二叉会出现在长度大于1的奇数长度区间下，而且出现位置为左右的偶数编号位置交替出现（如上图如果一个二叉就是在8号，两个就是8号和12号，三个就是8号，10号，12号…）

那么我们最后一层有2个节点，倒数第二层有n - 2个节点，倒数第三层有n - 3个节点，我们的最大编号为(n - 2 - 1 + (n - 2) / 2 + 1) * 2 * 1 + 1 = 3 * n - 5

同样的，当n = 2 ^ m + 2 * k ,(k = 1 , 2 , 3 …)

我们最大编号为(n - 2 * k - 1 + (n - 2k) / 2k * (2k - 1) + 1) * 2 + 1 = (4 - 1/k) * n - (8*k - 3) < 4 * n

故开辟4*n个节点

三、线段树的操作

3.1 单点修改

类似于平衡树的查找，不断缩小查询范围，根据区间往下递归即可

void update(int p, int x, int k) // 在p为根的树中找到x，加上k
{if (tree[p].l == x && tree[p].r == x) // 找到了叶子{tree[p].sum += k;return;}int m = (tree[p].l + tree[p].r) >> 1;if (x > m)update(rc, x, k);elseupdate(lc, x, k);tree[p].sum = tree[lc].sum + tree[rc].sum;
}

3.2 单点查询

和单点修改差不多。

// 单点查询
int query(int p, int x)
{if (tree[p].l == x && tree[p].r == x) // 找到了叶子return tree[p].sum;if (x <= tree[lc].l)return query(lc, x);if (x >= tree[rc].l)return query(rc, x);assert(false);return -1;
}

3.3 区间查询

类似于treap的split和merge，例如区间[4 , 9]可以拆成[4 , 5] , [6 , 8] , [9 , 9]，合并这三个区间的值就是我们查询的结果。

区间查询过程如下：

1. 从根节点进入，开始递归查询[x , y]
2. 如果x <= l <= r <= y，那么我们直接当前节点的结果。
3. 否则，判断左右区间是否和查询区间有重叠，如果有，递归对应子树

// 区间查询
int query(int p, int x, int y)
{if (x <= tree[p].l && tree[p].r <= y)return tree[p].sum;int m = (tree[p].l + tree[p].r) >> 1, sum = 0;if (x <= m)sum += query(lc, x, y);if (y > m)sum += query(rc, x, y);return sum;
}

3.3 区间修改

如果我们执行区间长度次单点修改，那么我们的时间复杂度显然太高了，我们这里的处理方法是给

// 向上更新
void pushup(int p)
{tree[p].sum = tree[lc].sum + tree[rc].sum;
}
// 向下更新
void pushdown(int p)
{if (tree[p].add){tree[lc].sum += tree[p].add * (tree[lc].r - tree[lc].l + 1);tree[rc].sum += tree[p].add * (tree[rc].r - tree[rc].l + 1);tree[lc].add += tree[p].add;tree[rc].add += tree[p].add;tree[p].add = 0;}
}
// 区间修改
void update(int p, int x, int y, int k)
{if (x <= tree[p].l && tree[p].r <= y){tree[p].sum += k * (tree[p].r - tree[p].l + 1);tree[p].add += k;return;}int m = (tree[p].l + tree[p].r) >> 1;pushdown(p);if (x <= m)update(lc, x, y, k);if (y > m)update(rc, x, y, k);pushup(p);
}

四、动态开点线段树

递增分配器

template <class T>
class CachedObj
{
public:void *operator new(size_t s){if (!head){T *a = new T[SIZE];for (size_t i = 0; i < SIZE; ++i)add(a + i);}T *p = head;head = head->CachedObj<T>::next;return p;}void operator delete(void *p, size_t){if (p)add(static_cast<T *>(p));}virtual ~CachedObj() {}protected:T *next;private:static T *head;static const size_t SIZE;static void add(T *p){p->CachedObj<T>::next = head;head = p;}
};
template <class T>
T *CachedObj<T>::head = 0;
template <class T>
const size_t CachedObj<T>::SIZE = 10000;
class Node : public CachedObj<Node>
{
public:Node *left;Node *right;int add;bool v;
};

动态开点线段树模板，其实就是把原来节点里存的区间放到函数参数里面了

#define int long long
int a[500010], n, m;
template <class T>
class CacheObj
{
public:void *operator new(size_t){if (!head){T *a = new T[SIZE];for (size_t i = 0; i < SIZE; i++)add(a + i);}T *p = head;head = head->CacheObj<T>::next;return p;}void operator delete(void *p, size_t){if (p)add(static_cast<T *>(p));}virtual ~CacheObj() {}protected:T *next;private:static T *head;static const size_t SIZE;static void add(T *p){p->CacheObj<T>::next = head;head = p;}
};
template <class T>
T *CacheObj<T>::head = nullptr;
template <class T>
const size_t CacheObj<T>::SIZE = 10000;
class Node : public CacheObj<Node>
{
public:Node() : left(nullptr), right(nullptr), sum(0), add(0) {}Node *left;Node *right;int sum;int add;
};
class SegmentTree
{
public:SegmentTree() : _root(new Node()){}SegmentTree(int l, int r) : _root(build(new Node(), l, r)){}Node *build(Node *p, int l, int r){p->sum = a[l];if (l == r)return p;int mid = (r + l) >> 1;p->left = build(new Node(), l, mid);p->right = build(new Node(), mid + 1, r);pushup(p);return p;}int query(int x){return query(x, 1, n, _root);}int query(int x, int l, int r, Node *node){if (l == x && r == x)return node->sum;int mid = (r + l) >> 1;pushdown(node, l, r, mid);if (mid >= x)return query(x, l, mid, node->left);return query(x, mid + 1, r, node->right);}int query(int left, int right){return query(left, right, 1, n, _root);}int query(int left, int right, int l, int r, Node *node){if (left <= l && r <= right){return node->sum;}int mid = (r + l) >> 1, ret = 0;pushdown(node, l, r, mid);if (mid >= left)ret += query(left, right, l, mid, node->left);if (mid < right)ret += query(left, right, mid + 1, r, node->right);return ret;}void pushup(Node *p){p->sum = p->left->sum + p->right->sum;}void pushdown(Node *p, int l, int r, int mid){if (!p->left)p->left = new Node();if (!p->right)p->right = new Node();if (p->add){p->left->add += p->add;p->left->sum += p->add * (mid - l + 1);p->right->add += p->add;p->right->sum += p->add * (r - mid);p->add = 0;}}void update(int x, int k){update(x, 1, n, k, _root);}void update(int x, int l, int r, int k, Node *node){if (r == x && l == x){node->sum += k;node->add += k;}int mid = (r + l) >> 1;if (x <= mid)update(x, l, mid, k, node);elseupdate(x, mid + 1, r, k, node);}void update(int l, int r, int k){update(l, r, k, 1, n, _root);}void update(int left, int right, int k, int l, int r, Node *node)// l , r 是当前节点的区间{if (left <= l && r <= right){node->add += k;node->sum += k;return;}int mid = (r + l) >> 1;pushdown(node, l, r, mid);if (mid >= left)update(left, right, k, l, mid, node->left);if (mid < right)update(left, right, k, mid + 1, r, node->right);pushup(node);}private:Node *_root;
};