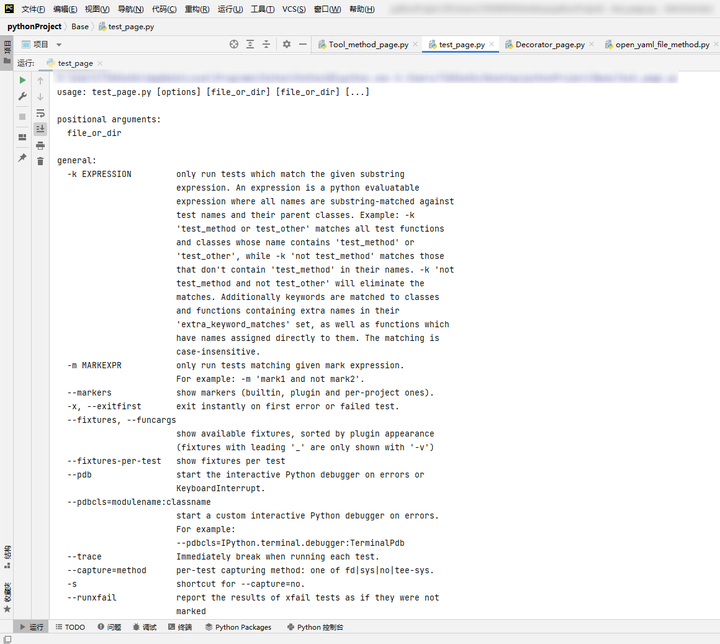
问题
今天做李六第一套的时候发现,有的时候,面对这种第二问的题,很自然地就想到了Fz(z),然后进行化简,但是有的时候,像这道题,就突然发现P{XY<z}是一个非常复杂的形式,根本没办法算。然而,看答案后发现,是一种不那么熟悉,但确实也是使用过的手法,也就是先求联合概率密度,再求分布函数(用二重积分进行积分),最后求导得出概率密度。然而,我感觉这两种方法有的时候不是一个脑回路(很奇怪),一个思路卡住,很难转变到另一个思路。初步猜测是由于随机变量的种类不同导致了这种区别,在此通过观察不同题的特点进行如下思考总结。
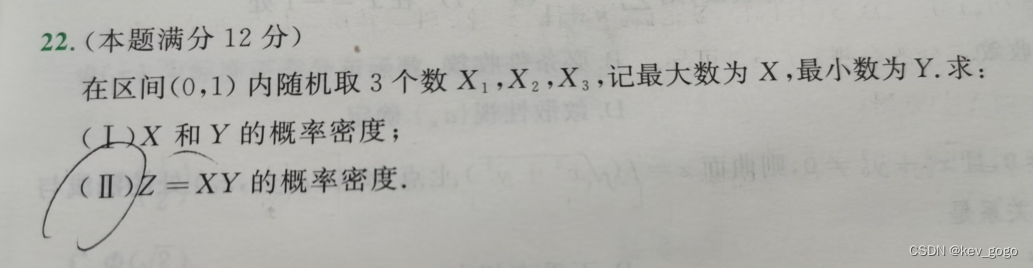
思考
对于离连型随机变量的通法:
- 求Z的分布函数(通过事件的性质进行化简)
- 求Z的概率密度
对于连续型随机变量的通法:
- 求x,y联合概率密度
- 通过二重积分求出Z的分布函数
- 求出Z的概率密度
事实上离散连续型的特点一般是概率密度已知然后通过化简可以把(有时因为独立,可以化简,有时不独立)离散型的变量划掉,最后变成单变量的分布函数(即边缘概率分布)而这一般比较好求得(通过分段相加的方法(注意:有时中间式子求导即可得到最终概率密度)),因此直接就可求导得到Z的概率密度。
而连续连续型,往往给的条件比较少,而且最关键的是,如果X和Y,其中一个不能用另一个来表示,那么一定要化成二重积分的形式(因为化成不了边缘概率),而2021年数一的概率题比较简单就在于其虽然是连续连续型概率密度,依旧可以用离连型分布来解决(因为Y可以用X表示来化成边缘概率密度)
总结
离散连续型优先考虑直接上FZ(z),并化简。连续连续型,如果Y和X存在表示关系,则用离连型的方法,如果不存在互表关系,则采用联合概率密度加二重积分的方式。
自从16年之后,考这种多维随机变量的题特别多,而离散离散,离散连续都考过多次,连续连续目前我做到21年,仅出现了较简单的形式, 而不可互表的形式目前仅在模拟题中看到,而这种题也是完全完全在偶数年大概率可以出现的,一定要拿下。