1.模式匹配

给出字符串’abacacaaad’在KMP算法中的next和nextval数组。

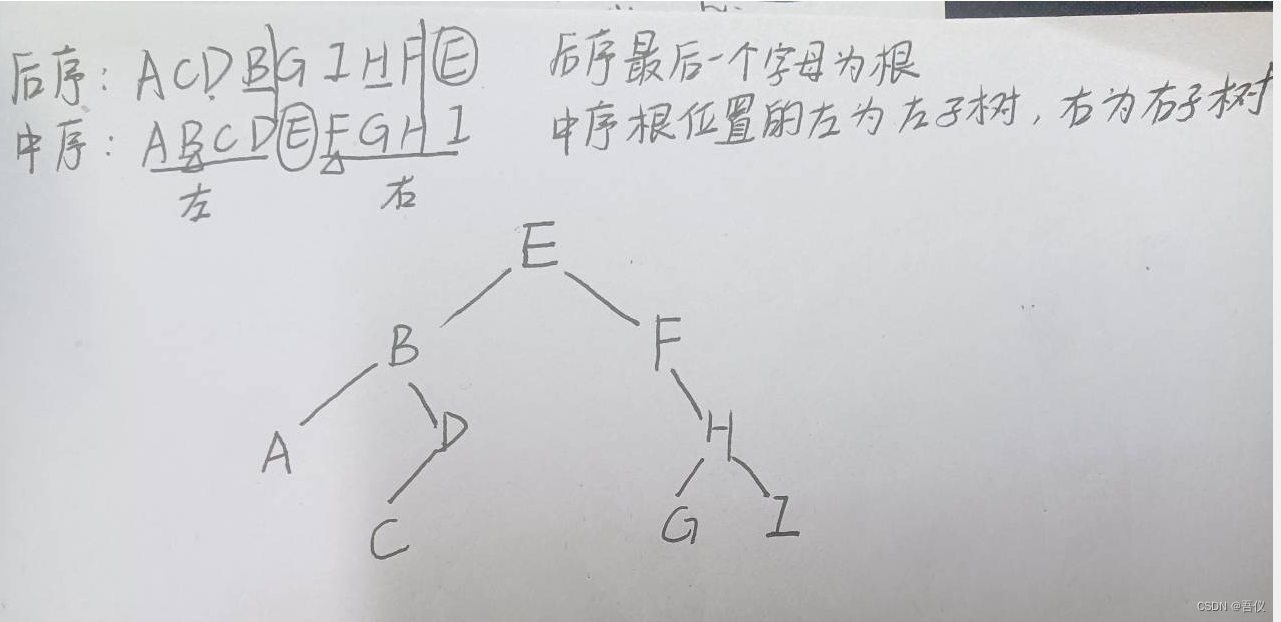
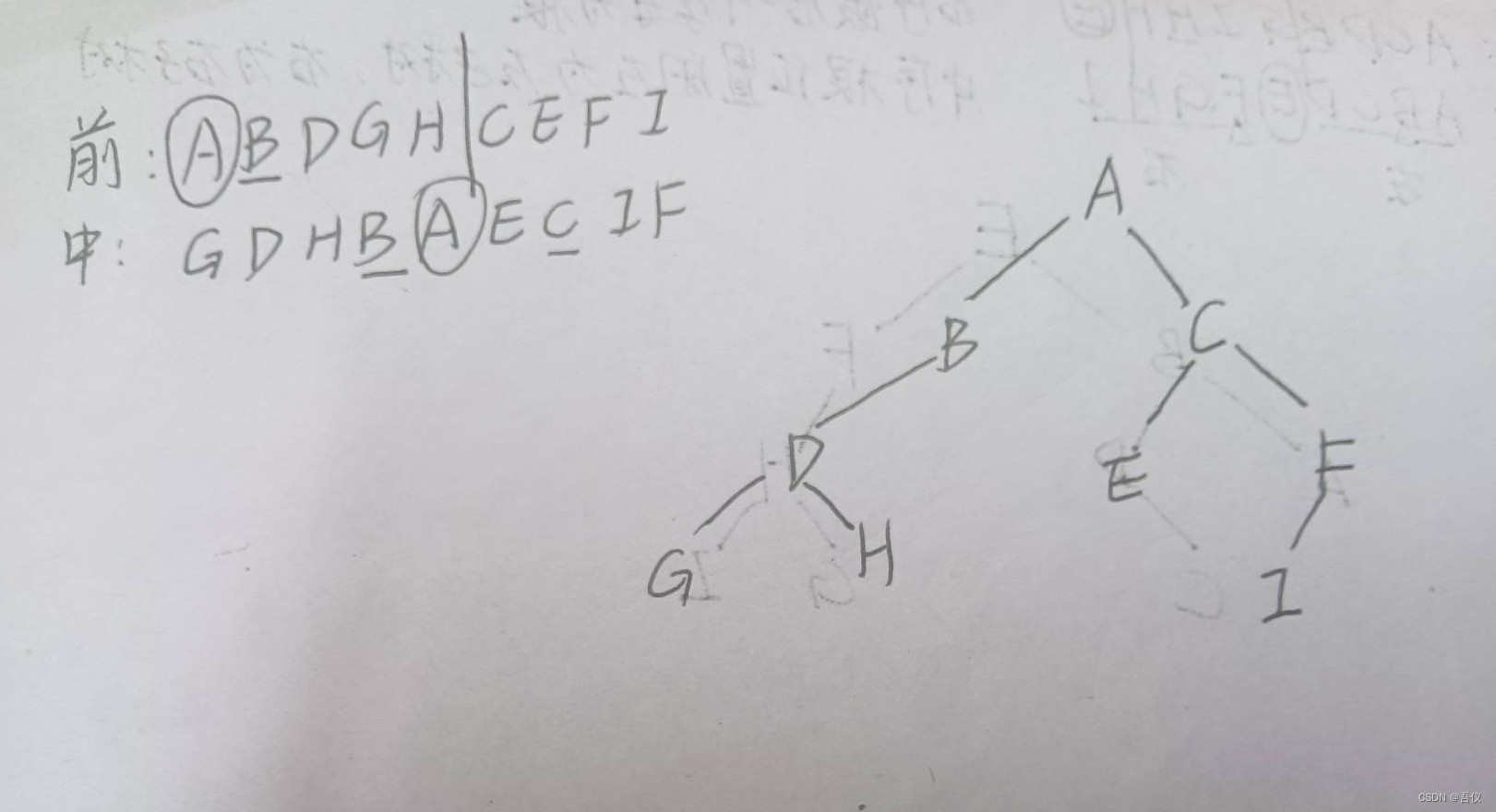
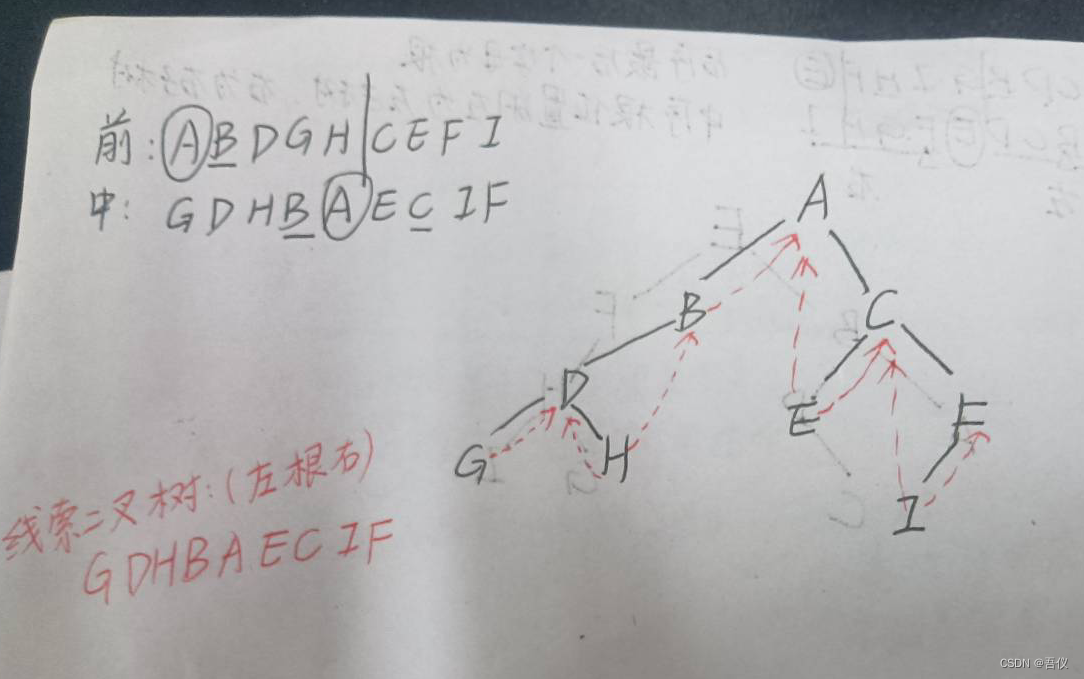
2.画二叉树（根据中序和后序，前序和中序）及其线索二叉树

2.1已知一棵二叉树的后序遍历和中序遍历的序列分别为：

2.2已知一棵二叉树的前序遍历和中序遍历的序列分别为：

线索二叉树

3.求叶子结点个数

已知一颗度为3的树中，有度数为3的结点100个，度数为2的结点200个，求叶子结点的个数，并给出推导过程。

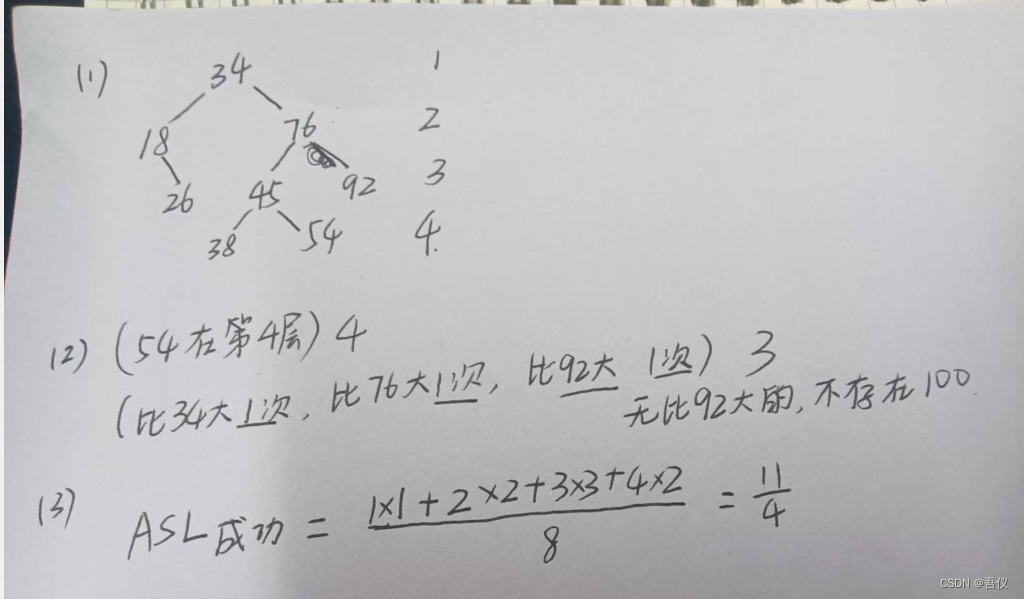
4.建立二叉排序树

对于给定结点的关键字集合K=[34，76，45，18，26，54,92,38]
（1）试构建一棵二叉排序树（2）查找54需要比较几次？查找100的比较次数？（3）求等概率情况下查找成功的平均查找长度ASL

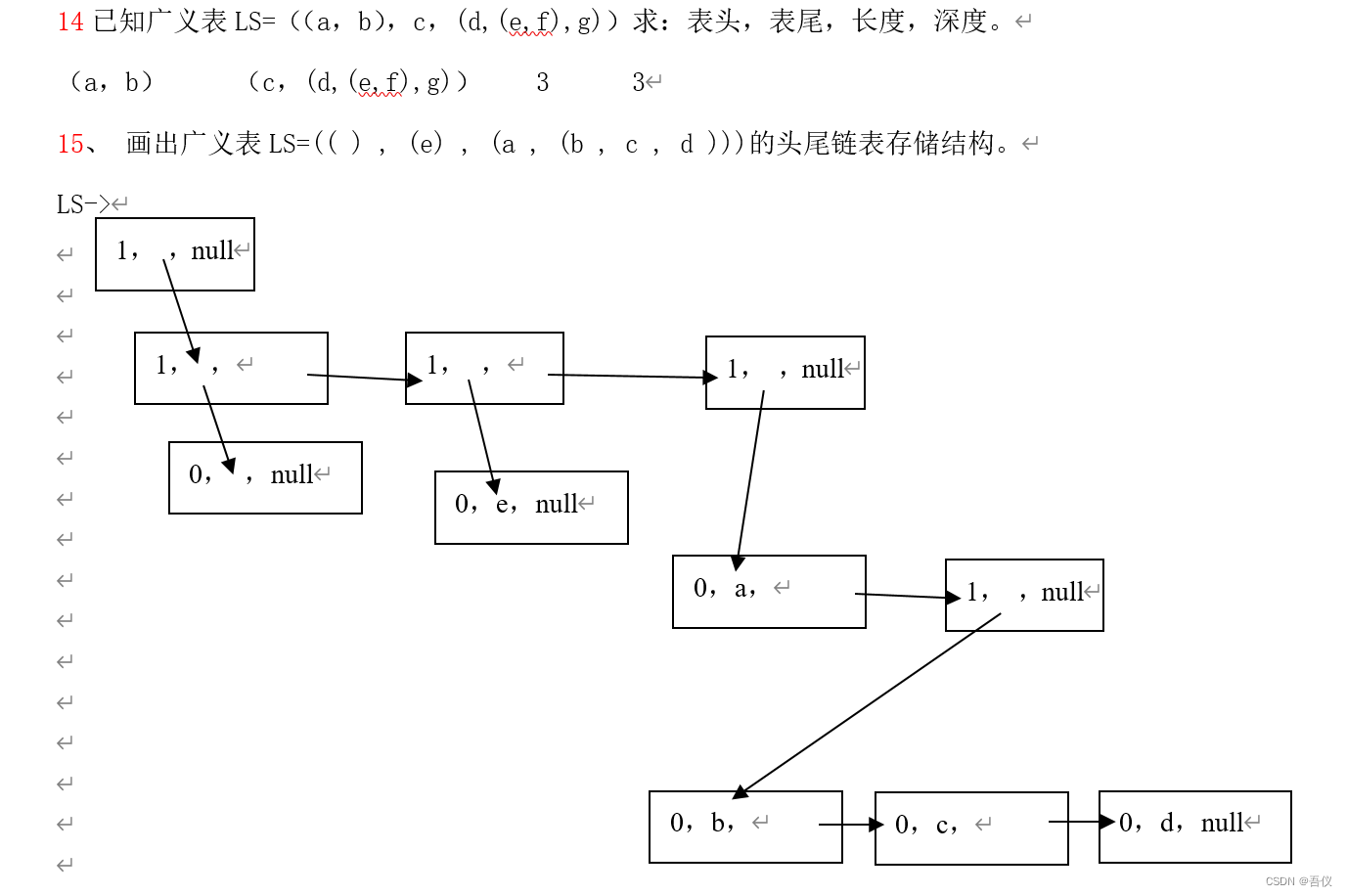
5.广义表

6.求存储地址

数组元素a[0…2][0…3]的首地址为2000，元素长度为4，求LOC[1,2].
LOC【1,2】=2000+（i*n+j）*k （n为二维数组列的个数，k为元素长度）i=1 j=2

7.代码设计

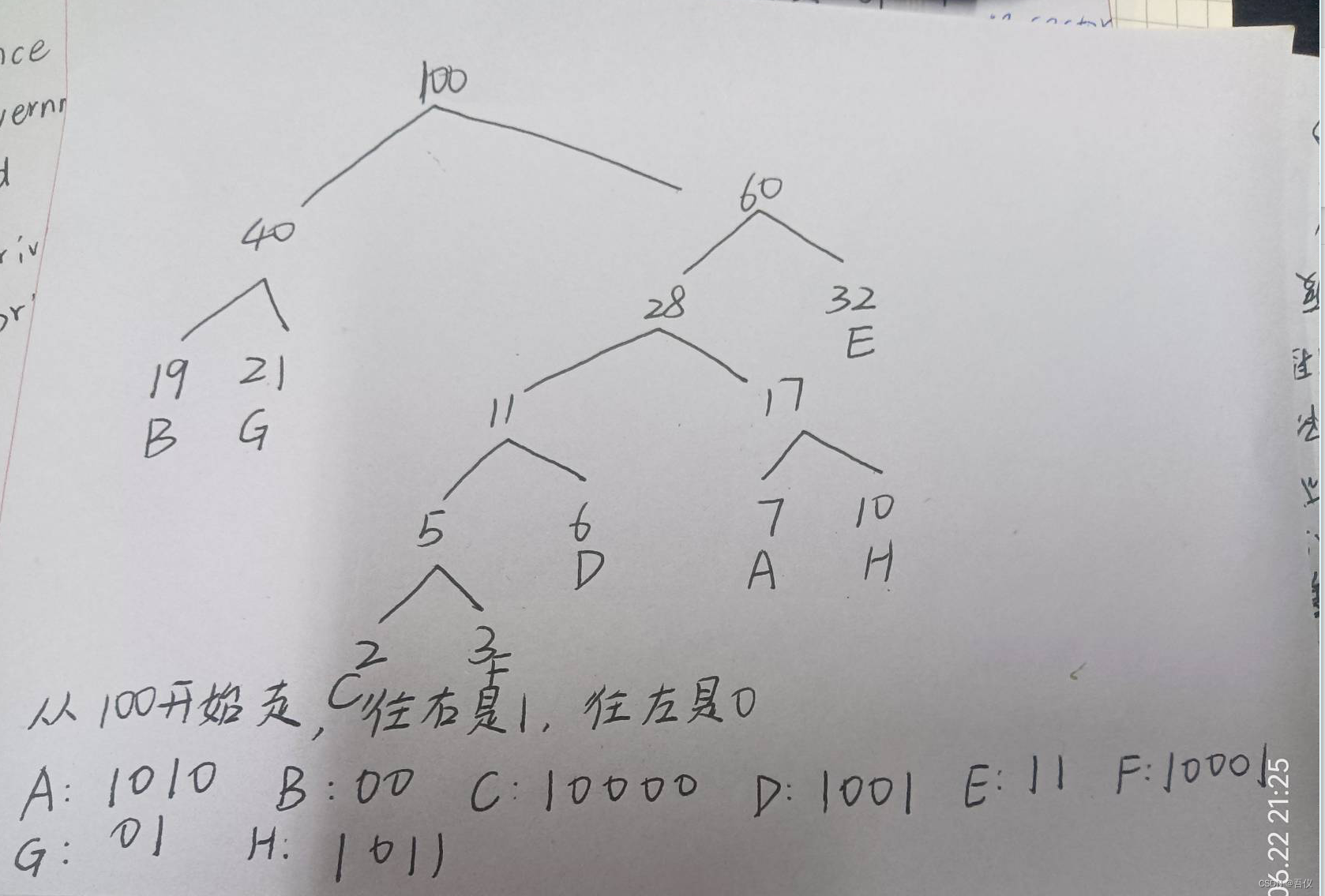
8.哈夫曼树

假设用于通信的电文仅由A、B、C、D、E、F、G 8个字母组成，字母在电文中出现的频率分别为7，19，2，6，32，3，21，10。试为这8个字母设计哈夫曼树及哈夫曼编码。

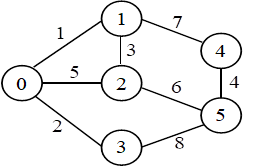
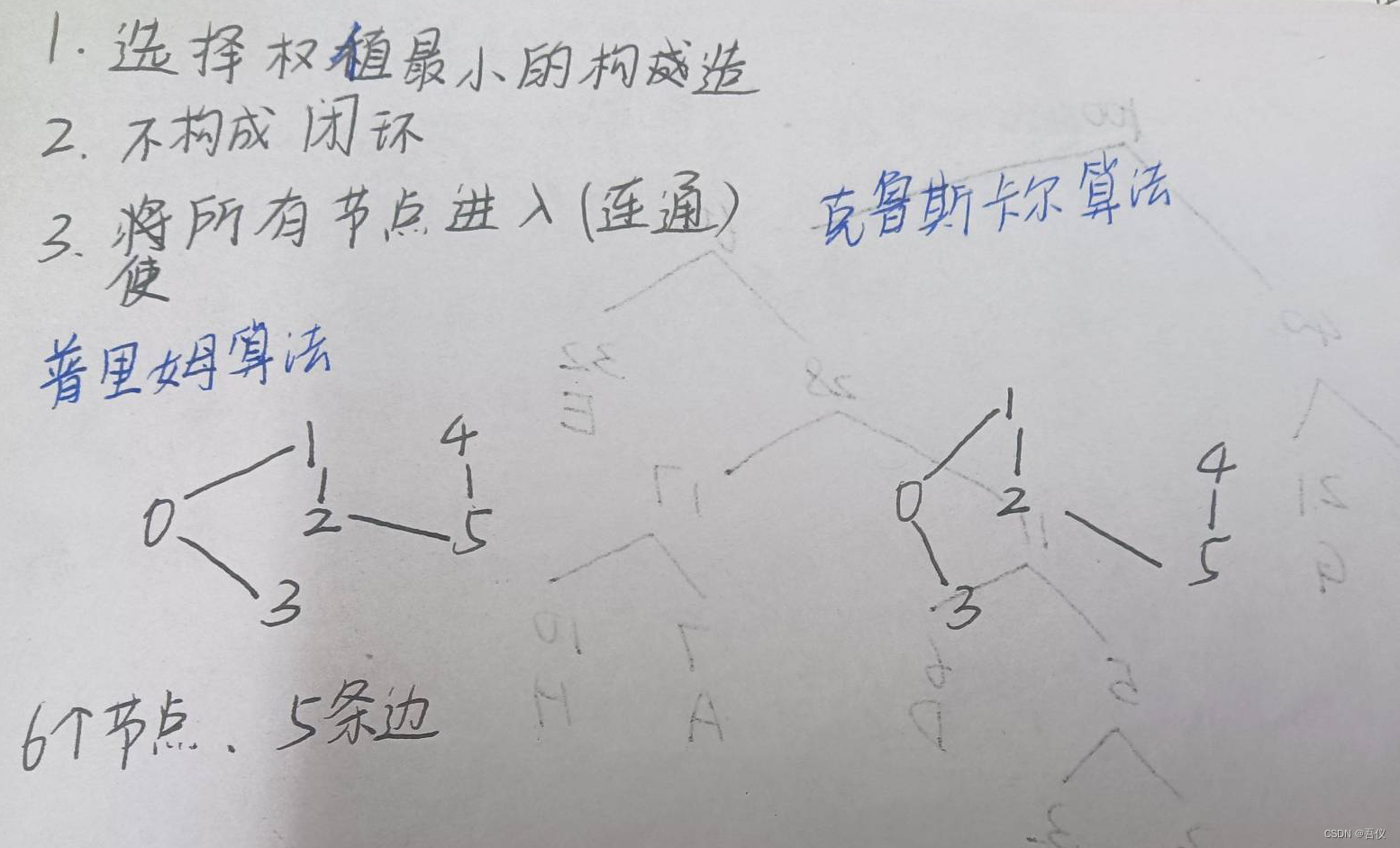
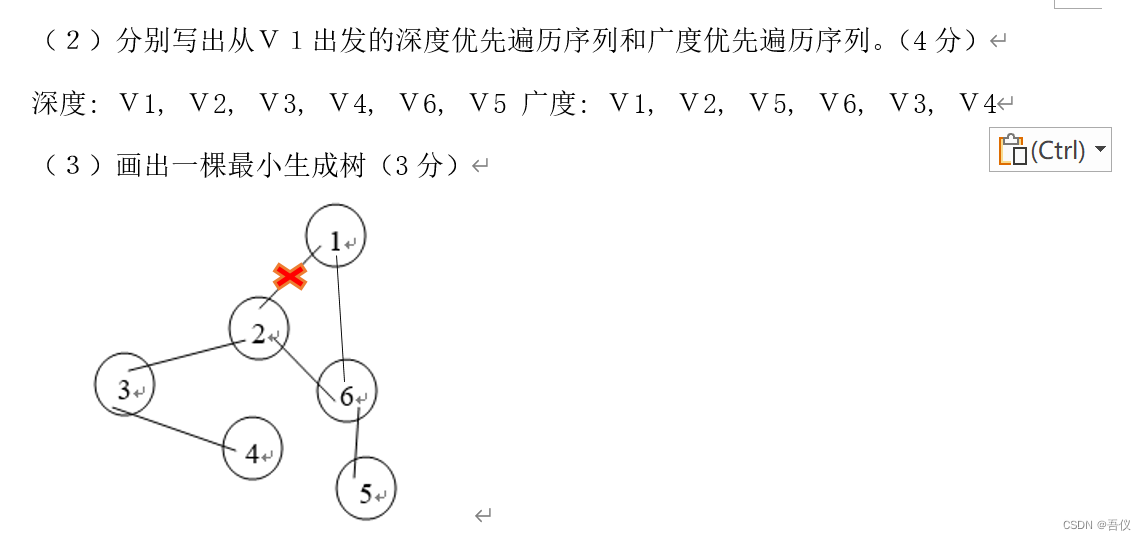
9.最小生成树

对于下图所示的带权无向图，给出利用普里姆算法（从顶点0开始构造）和克鲁斯卡尔算法构造出的最小生成树，并按求解的顺序给出最小生成树的所有边，每条边用(i，j)表示）。

{(0,1),(0,3),(1,2),(2,5),(5,4)}
{(0,1),(0,3),(1,2),(4,5),(2,5)}

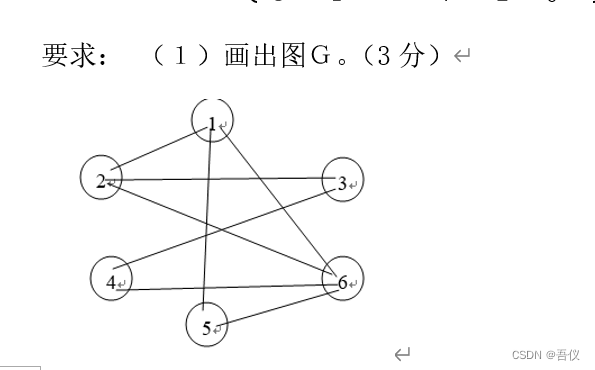
带权无向图Ｇ（顶点分别为Ｖ１，Ｖ２，Ｖ３，Ｖ４，Ｖ５，Ｖ６）的邻接矩阵是Ａ

10.深度遍历、广度遍历、邻接表建立

11.哈希表（线性探测法、拉链法）

设哈希表的长度ｍ＝13；哈希函数为H(K)=K%m，给定的关键码序列为19，14，23，01，68，20，84，27，55，11，试填出用线性探查法和链地址法解决冲突时所构造的哈希表。并求在每种哈希表上成功查找的ASL。

12.排序

已知关键字序列为 (34,23,56,32,45,58,89,20,25,50)，分别用下列排序方法进行排序，分别写出每趟排序结果，并指出算法的稳定性。1）快速排序 2）希尔排序 3）堆排序
(1)
(25,23,20,32,34,58,89,45,56,50)
(20,23,25,32,34,50,56,45,58,89)
(20,23,25,32,34,45,50,56,58,89) 划分的子表为1或0停止即可
不稳定
(2)
(34,23,20,25,45,58,89,56,32,50)
(20,23,32,25,34,50,45,56,89,58)
(20,23,25,32,34,45,50,56,58,89)
不稳定
(3)
(58,50,56,32,45,34,23,20,25,89)
(56,50,34,32,45,25,23,20,58,89)
(50,45,34,32,20,25,23,56,58,89)
(45,32,34,23,20,25,50,56,58,89)
(34,32,25,23,20,45,50,56,58,89)
(32,23,25,20,34,45,50,56,58,89)
(25,23,20,32,34,45,50,56,58,89)
(23,20,25,32,34,45,50,56,58,89)
(20,23,25,32,34,45,50,56,58,89)
不稳定