文章目录
- 1. 引言
- 2. 快速排序算法
- 2.1 传统快速排序
- 2.2 三者取中法
- 3. 实验内容
- 3.1 实验题目
- (一)输入要求
- (二)输出要求
- 3.2 算法实现
- 4. 实验结果
1. 引言
快速排序是一种经典的排序算法,其核心思想是通过选择一个基准元素,将数组分为两个部分,左边的元素小于基准,右边的元素大于基准,然后对左右两部分递归地进行排序。然而,在处理基本有序数组时,传统的快速排序可能会退化为 O ( n 2 ) O(n^2) O(n2)的时间复杂度。为了解决这个问题,引入了三者取中法,通过选择数组中的三个元素并取其中值作为基准元素,能够在基本有序的情况下提高排序效率。
2. 快速排序算法
2.1 传统快速排序
快速排序的核心思想是通过选择一个基准元素,将待排序的数组划分为两个部分,左边的元素小于基准,右边的元素大于基准,然后对左右两部分递归地进行排序,其时间复杂度:
- 最好情况: 每次分划都能将数组平均地划分成两部分,此时的时间复杂度为 O ( n l o g 2 n ) O(n log_2 n) O(nlog2n)。
- 最坏情况: 每次分划都选择了数组中最小(或最大)的元素作为基准,导致每次分划只能减少一个元素,时间复杂度 O ( n 2 ) O(n^2) O(n2)。
- 平均情况: 通过概率分析,可以证明时间复杂度为 O ( n l o g 2 n ) O(n log_2 n) O(nlog2n)。
2.2 三者取中法
2. 算法描述:
改进的快速排序算法主要区别在于基准元素的选择。在传统快速排序中,通常选择随机元素作为基准,而在改进算法中则采用三者取中法:

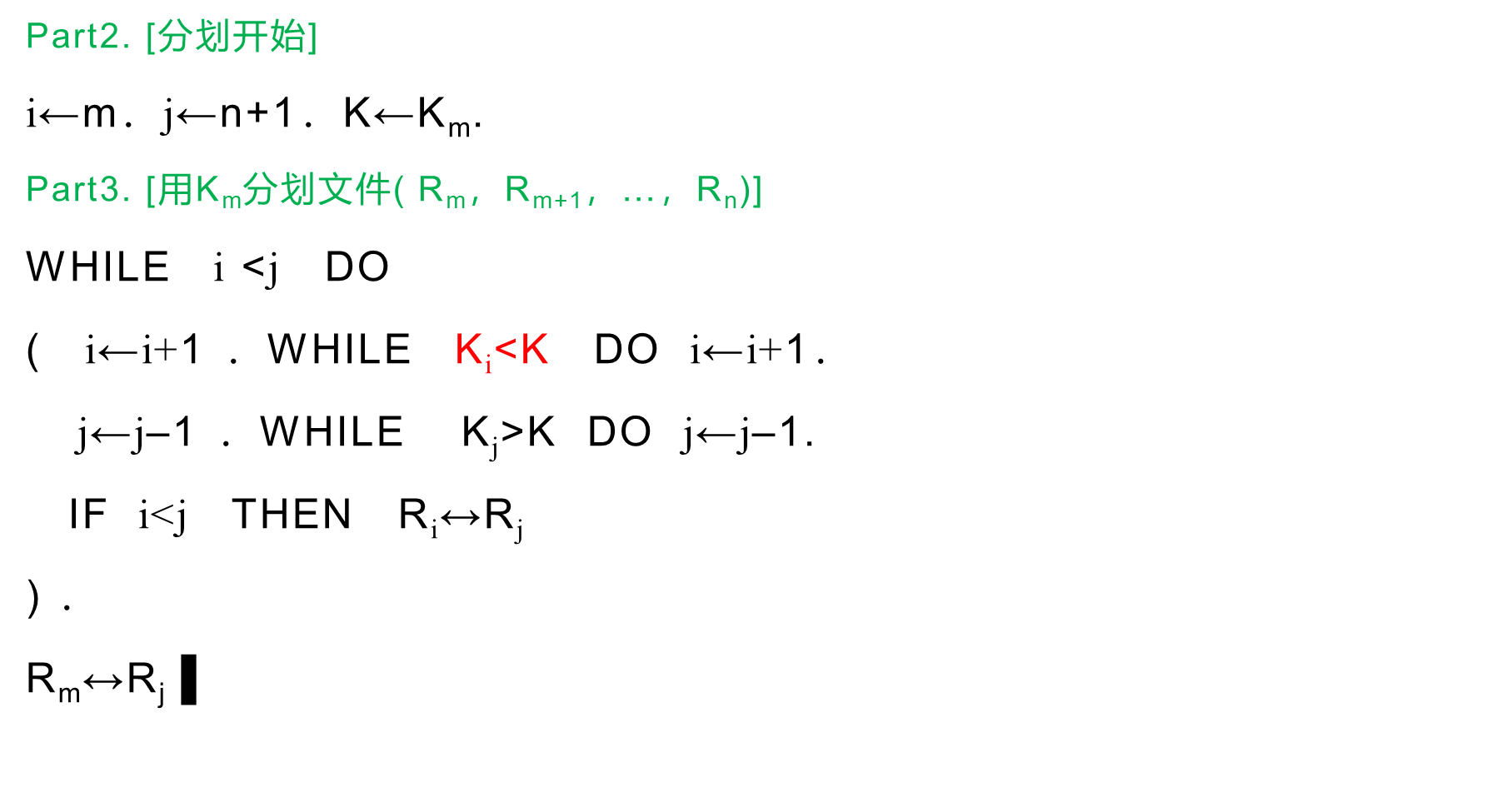
3. 实验内容
3.1 实验题目
实现教材233 页下方提及的 Select 算法(求第 4 小元素)(要求文件长度大于等于 5 时调用 Partition2 算法,否则调用直接插入排序算法)。
(一)输入要求
第一组输入数据:
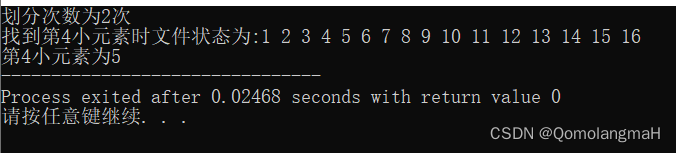
{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16}
第二组输入数据:
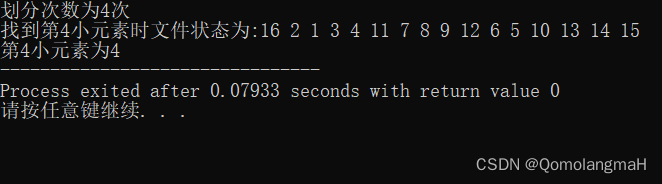
{16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1}
(二)输出要求
对每组输入数据,输出以下信息(要求必须要有关于输出数据的明确的提示信息):
- 输出分划次数;
- 输出找到第 4 小元素时文件的状态,即输出此时所有记录的值。
3.2 算法实现
#include<stdio.h>
void Change(int R[],int i,int j)
{int t=R[i];R[i]=R[j];R[j]=t;
}
int Partition2(int R[],int m,int n)
{Change(R,(m+n)/2,m+1);if(R[m+1]>R[n]) Change(R,m+1,n);if(R[m]>R[n]) Change(R,m,n);if(R[m+1]>R[m]) Change(R,m + 1,m);int i=m,j=n+1,K=R[m];while(i<j){i++;while(R[i]<=K) i++;j--;while(R[j]>K) j--;if(i<j)Change(R,i,j);}Change(R,m,j);return j;
}
void InsertSort(int R[],int len)
{int i,j,t;for(i=1;i<len;i++)if(R[i]<R[i-1]){t=R[i];R[i]=R[i-1];for(j=i-1;R[j]>t&&j>=0;j--){R[j+1]=R[j];}R[j+1]=t;}
}
int Select(int R[], int n)
{if(n>=5){int t=Partition2(R,1,n),rounds=0;rounds++;while(t!=4){if(t<4) t=Partition2(R,t+1,n);else t=Partition2(R,1,t-1);rounds++;}printf("分划次数为%d次\n",rounds);printf("找到第4小元素时文件状态为:");int i;for(i=0;i<n;i++)printf("%d ",R[i]);printf("\n");return R[4];}else{InsertSort(R,n);return R[4];}
}
int main()
{//int R[16]={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};int R[16]={16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1};printf("第4小元素为%d",Select(R,16));return 0;
}Change函数用于交换数组中的两个元素。Partition2函数使用中值法选择主元,并使用修改过的Lomuto分区方案对数组进行分区。它返回选择的主元的最终位置。InsertSort函数对数组执行插入排序。Select函数是主要的算法。如果数组的大小大于或等于5,它使用Partition2函数递归地找到第4小元素。如果大小小于5,它使用InsertSort函数对数组进行排序,并返回第4个元素。
4. 实验结果