1 离散型随机变量
1.1 0-1分布
设随机变量X的所有可能取值为0与1两个值,其分布律为
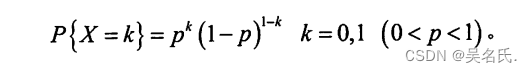
若分布律如上所示,则称X服从以P为参数的(0-1)分布或两点分布。记作X~ B(1,p)
0-1分布的分布律利用表格法表示为:
| X | 0 | 1 |
|---|---|---|
| P | 1-P | P |
0-1分布的数学期望E(X) = 0 * (1 - p) + 1 * p = p
1.2 二项分布
二项分布的分布律如下所示:
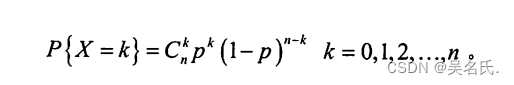
其中P是事件在一次试验中发生的概率,称随机变量X服从参数为n,p 的二项分布,记作X~B(n,p)。当n=1时,X为(0-1)分布
二项分布利用表格法也可表示为:
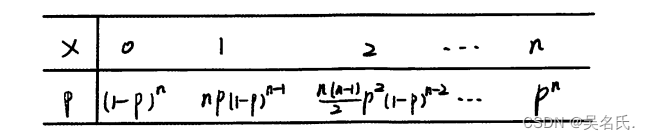
二项分布的数学期望E(X) = np
1.3 泊松分布
设随机变量X所有可能取值是0,12,…,而取各个值的概率为
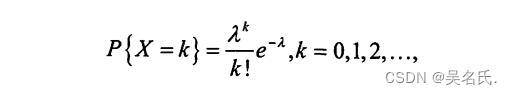
其中λ>0是常数,则称随机变量 X 服从泊松分布,记为 X ~ π(λ)
泊松分布利用表格法可表示为:

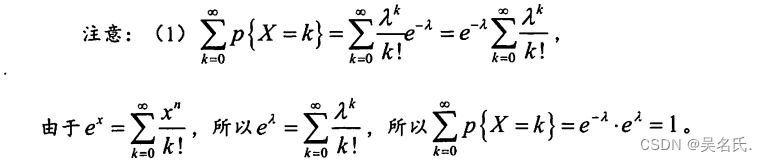
泊松分布的数学期望E(X) = λ
泊松分布的方差D(X) = λ
1.4 几何分布
记X在独立重复试验中事件A首次发生所进行试验的次数,则
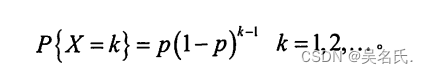
我们称随机变量X服从几何分布,记作X~G§。
几何分布利用表格法也可表示为:

几何分布的数学期望E(X) = 1/p
几何分布的方差D(X) = (1-p)/(p*p)
1.5 超几何分布
设有N件产品,其中有M(MSN)件次品。从中任取n(nN)件产品,用X表示取出的n件产
品中次品的件数,则
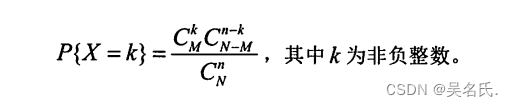
我们称随机变量X服从参数为N、M、n的超几何分布
注意:超几何分布为不放回抽样。
2 连续性随机变量
2.1 均匀分布
2.1.1 均匀分布的密度函数
若连续型随机变量X的概率密度
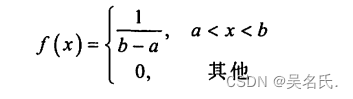
则称f(x)在(a,b)上服从均匀分布,记作X~U(a,b)
2.1.2 均匀分布的分布函数及图像
均匀分布的分布函数为:
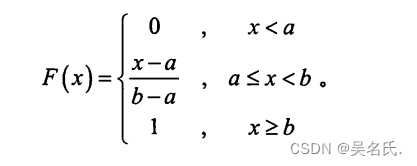
f(x)与F(x)分别如图所示:
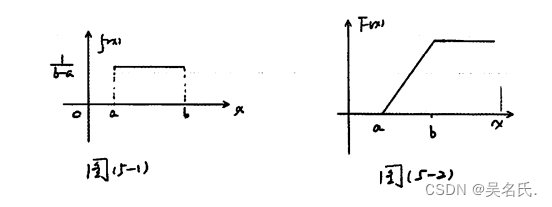
2.1.3 均匀分布的数学期望及其方差
均匀分布的数学期望E(X) = ( a + b ) / 2
均匀分布的方差D(X) = (( b - a ) ^ 2) / 12
2.2 指数分布
2.2.1 指数分布的概率密度
若连续型随机变量X概率密度为:
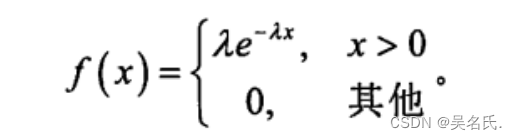
其中λ>0为常数,则称X 服从参数为的指数分布。记作X~ E(λ)
2.2.2 指数分布的分布函数及图像
随机变量X的分布函数和图像为:
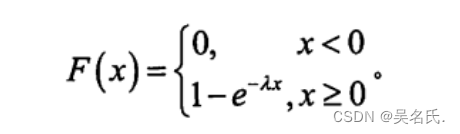
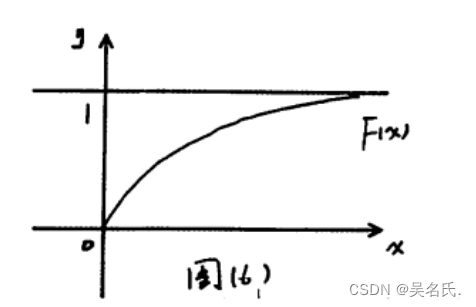
2.2.3 指数分布的数学期望及其方差
指数分布的数学期望E(X) = 1 / λ
指数分布的方差D(X) = 1 / (λ ^ 2)
2.3 正太分布
2.3.1 一般正太分布的密度函数、分布概率及其图像
若连续型随机变量X的概率密度和图像为:
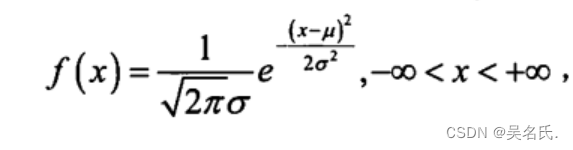
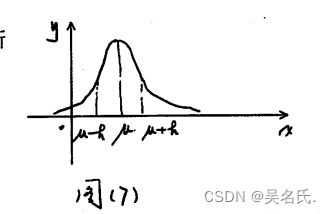
其中μ,σ( σ > 0)为常数,则称服从参数为,的正态分布,记作X~ N(μ, σ * σ),分布函数为:
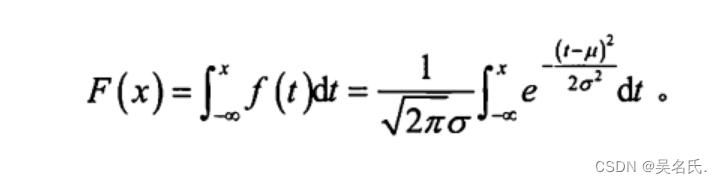
2.3.2 标准正太分布的密度函数、分布概率及其图像
当参数 u=0,σ=1时称随机变量X 服从标准正态分布,记作X~N(0,1)。其概率密度及分布函数如下所示:
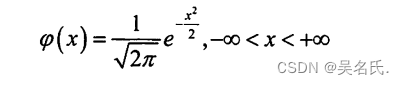
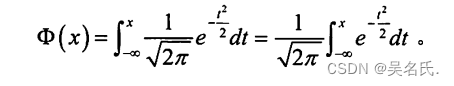
概率密度图像如下所示:
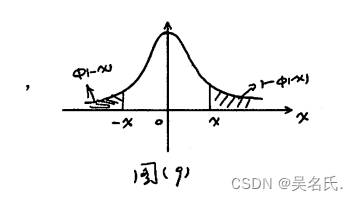
其概率密度函数的图形如图 (9)所示。由(x)的图形,不难得出如下性质:
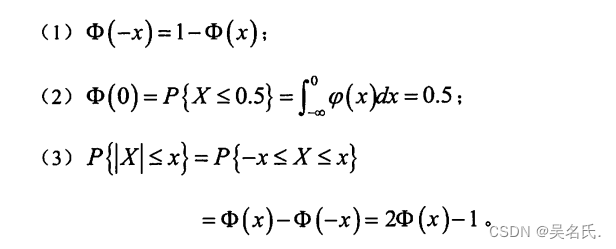
2.3.3 正太分布的数学期望及其方差
正太分布的数学期望E(X) = u
正太分布的方差D(X) = σ
3 数学期望的性质
下面给出数学期望常见的性质:
- 设C是常数,则有E©=C。
- 设X是一个随机变量,C为常数,则有 E(CY)=CE(Y)
- 设X,Y为两个随机变量,则E(XY)=E(Y)E(Y)
- 设X,Y 为相互独立的随机变量,则 E(XY)=E(Y)·E(Y)
数学期望E(X)和方差D(X)之间的关系:
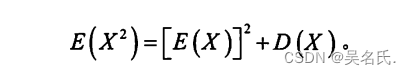
4 方差
4.1 方差的性质
-
设C为常数,则D©=0。
-
@设X是随机变量,C是常数,则有 D(CX)=C^2D(X),D(X+C)=D(X)
-
设XY是两个随机变量,则有
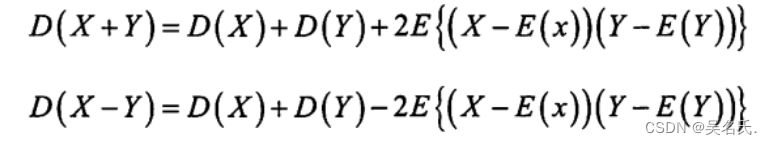 特别地,若X与Y相互独立,则有D(X+Y)=D(X)+D(Y),D(X-Y)=D(X)+D(Y)
特别地,若X与Y相互独立,则有D(X+Y)=D(X)+D(Y),D(X-Y)=D(X)+D(Y) -
D(Y)=0的充分必要条件是以概率为1 取常数 E(X),即P{ X=E(X) } = 1
4.2 协方差和相关系数
协方差公式: cov(X,Y) = E(XY) - EXEY
协方差公式的几个变形:
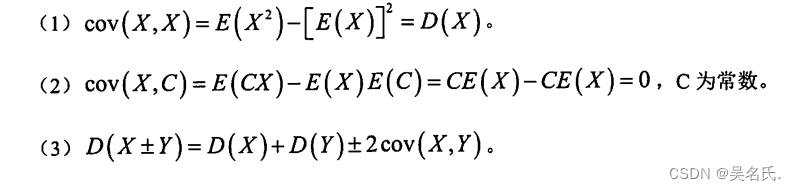
相关系数ρxy公式如下:
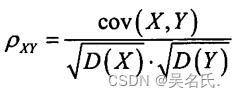


![[AutoSAR 存储] 汽车智能座舱的存储需求](https://img-blog.csdnimg.cn/6eb729919b834c13bc5f03df4bf5afc3.png)