目录

一、全概率公式

二、贝叶斯公式

三、综合题目

---

一、全概率公式

  定义: 在事件A发生的前提下，事件A又作为事件B发生的条件，这样两两一组的概率总和，就为概率论公式。题目通常问的是一整个事件的概率。别急，请看例题。

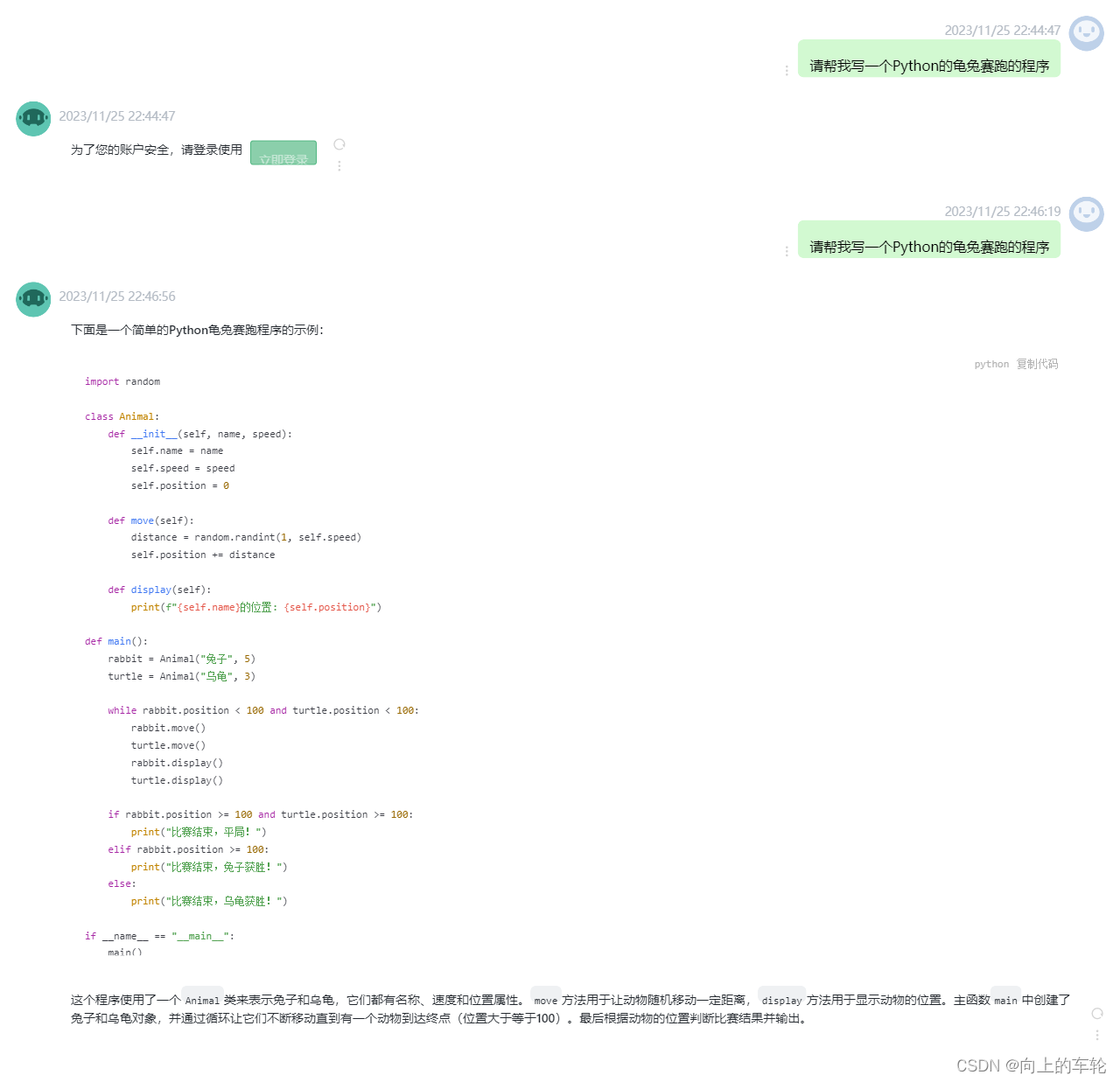
1.18  有两批相同的产品，第一批产品共14件，其中有2件为次品，装在第一个箱中，第二批有10件，其中有1件是次品。装在第二个箱中，今在第一箱中任意取出2件混入到第二箱中，然后再从第二箱中任取一件，求出第二箱中取到的是次品的概率。

  在从第一箱中取0件次品到第二箱中的前提下，从第一箱中取0件次品到第二箱中的前提又作为在第二箱取到次品的条件。这样两两一组的概率总和，就为概率论公式。从直观上也比较好理解，因为我们是先从第一箱中取出产品到第二箱中，再从第二箱中取出产品，那么先发生的是从第一箱中取出产品放到第二箱中，自然会作为从第二箱中取出产品的条件，但由于我们要先从第一箱中取出产品放到第二箱，所以还有乘P(从第一箱中取出产品放到第二箱中)。

1.19  一等小麦种子中混有5%的二等种子和3%的三等种子，已知从一、二、三等种子将来长出的穗有50颗以上麦粒的分别概率为50%、15%和10%。假设一、二、三等种子的发芽率相同，用上述的小麦种子播种后，这批种子所结的穗有50克以上麦粒的概率。

二、贝叶斯公式

 

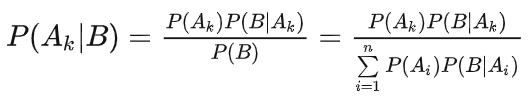
   定义: 在事件A发生的前提下，事件A又作为事件B发生的条件的概率/全概率就为贝叶斯公式。题目通常问的是一个事件发生的条件下另一个事件发的的概率。同样，先看题。

1.20  设男女两性人口之比是51 :49，男性中有5%是色盲患者，女性中有2.5%是色盲患者。今从人群中随机抽取一人，恰好是色盲患者，求此人为男性的概率。

三、综合题目