1. 引言

  图是一种常见的数据结构，用于表示对象之间的关系。在图的表示方法中，邻接表是一种常用的形式，特别适用于稀疏图。

本实验将介绍如何使用邻接表表示图，并通过C语言实现图的邻接表创建。

2. 邻接表表示图的原理

2.0 图的基础知识

a. 类型

  图（Graph）是由节点（Vertex）和节点之间的边（Edge）组成的一种数据结构。图可以用来表示不同对象之间的关系或连接方式。在图中，每个节点代表一个对象，而边则表示节点之间的关系或连接。根据边的性质，图可以分为有向图（Directed Graph）和无向图（Undirected Graph）两种类型。

• 有向图是指图中的边具有方向性，表示节点之间的单向关系。例如，如果节点A指向节点B的边存在，则从节点A可以到达节点B，但从节点B无法直接到达节点A。有向图中的边可以是单向的，也可以是双向的。

• 无向图是指图中的边没有方向性，表示节点之间的双向关系。无向图中的边是双向的，即从节点A可以到达节点B，同时从节点B也可以到达节点A。

b. 表示

  图可以用多种方式表示，常见的有邻接矩阵（Adjacency Matrix）和邻接表（Adjacency List）两种形式。

• 邻接矩阵是一个二维数组，用于表示节点之间的连接关系。对于有向图，邻接矩阵的元素表示从一个节点到另一个节点的边的存在与否；对于无向图，邻接矩阵是对称的。

• 邻接表是一种链表数组的形式，用于表示每个节点和与之相连的边。对于每个节点，邻接表中存储了与该节点直接相连的所有节点的信息。

2.1 有向权图

  有向权图（Directed Weighted Graph）是指图中的边具有方向性和权重（Weight），表示节点之间的单向关系以及边的权值。每条边都有一个与之关联的权重，用于表示节点之间的某种度量或成本。

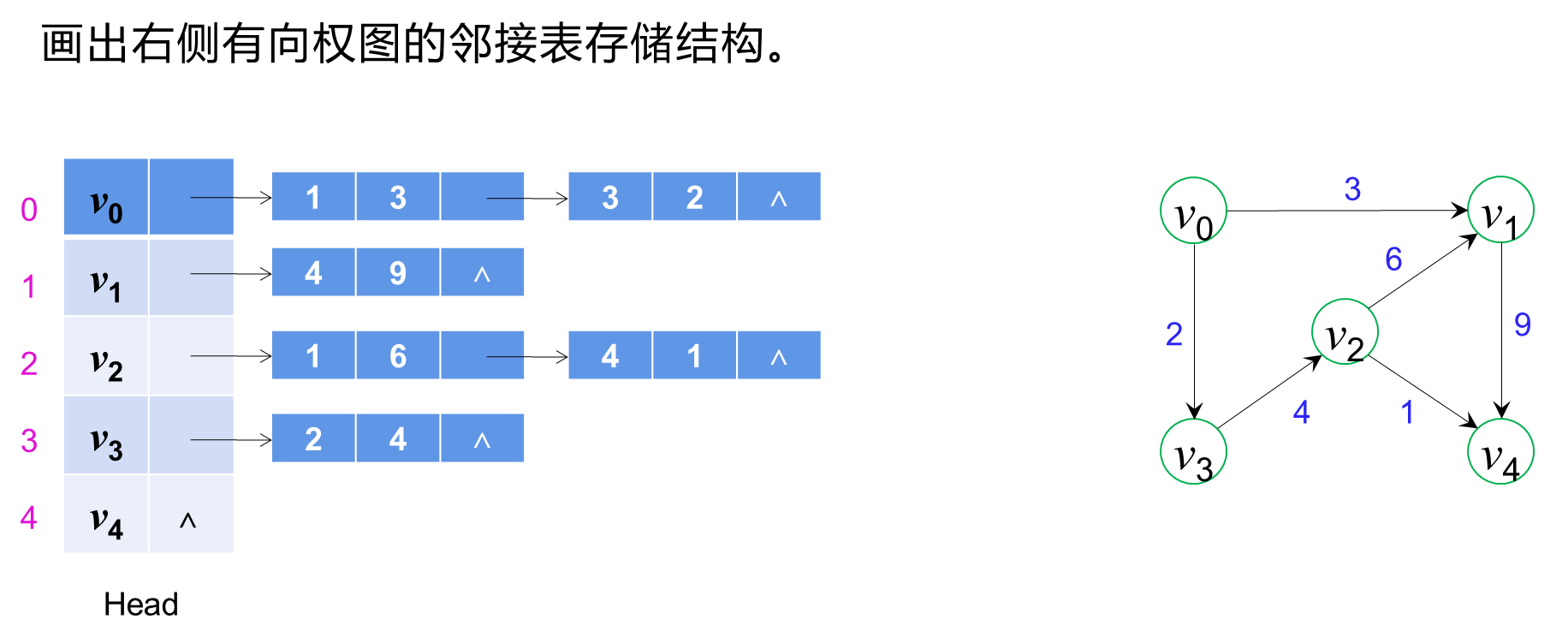
2.2 无向权图

  无向权图（Undirected Weighted Graph）是指图中的边没有方向性但具有权重，表示节点之间的双向关系以及边的权值。无向权图中的边是双向的，权重可以用于表示节点之间的某种度量或成本。

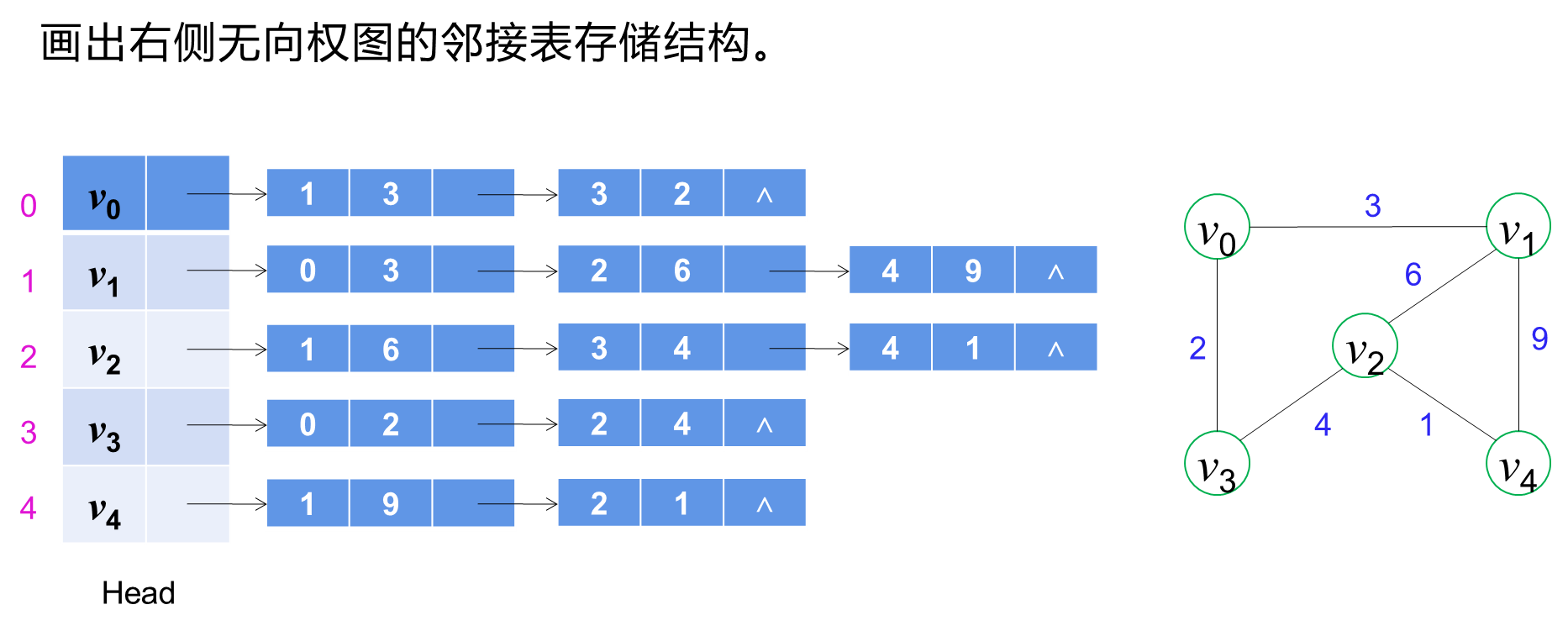
2.3 无向非权图

  无向非权图（Undirected Unweighted Graph）是指图中的边没有方向性也没有权重，表示节点之间的双向关系但没有额外的权值信息。无向非权图中的边是双向的，仅表示节点之间的连接关系，不含其他度量或成本信息。

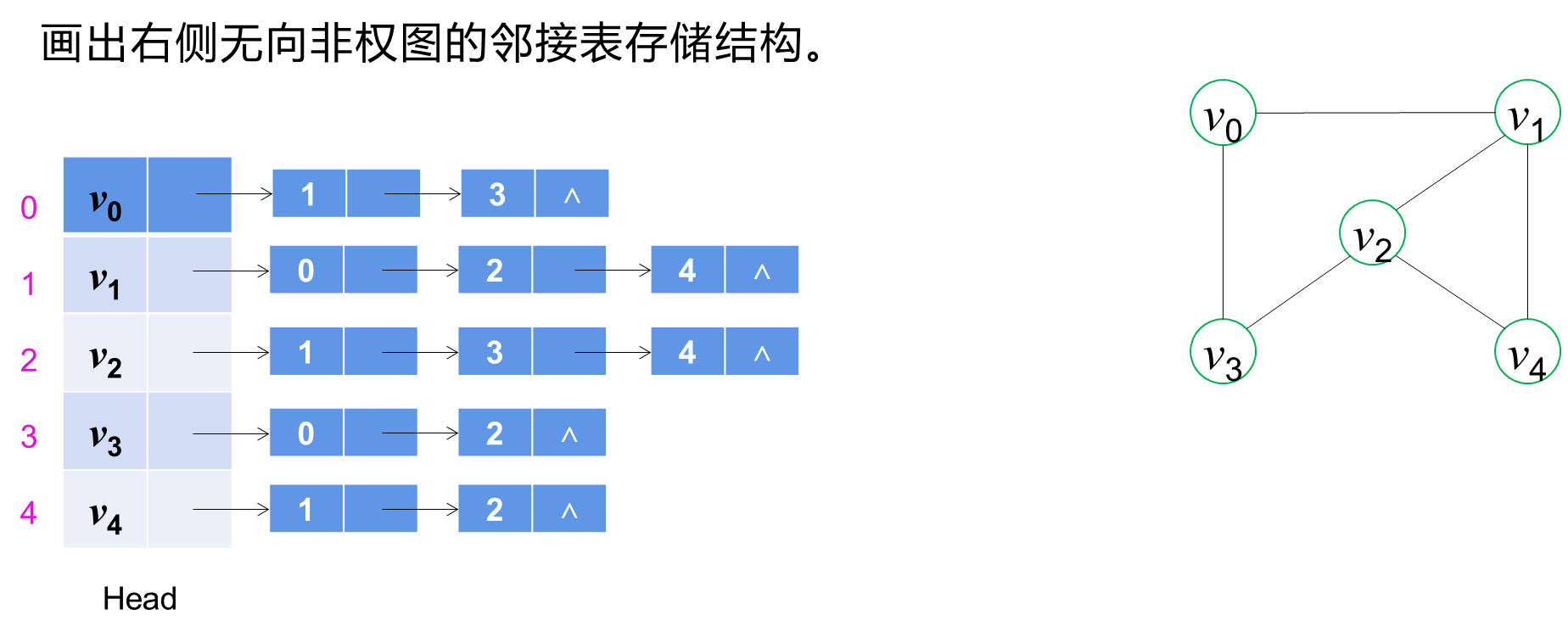
2.4 有向非权图

  有向非权图（Directed Unweighted Graph）是指图中的边具有方向性但没有权重，表示节点之间的单向关系但没有额外的权值信息。有向非权图中的边可以是单向的，表示从一个节点指向另一个节点的关系，但不包含其他度量或成本信息。

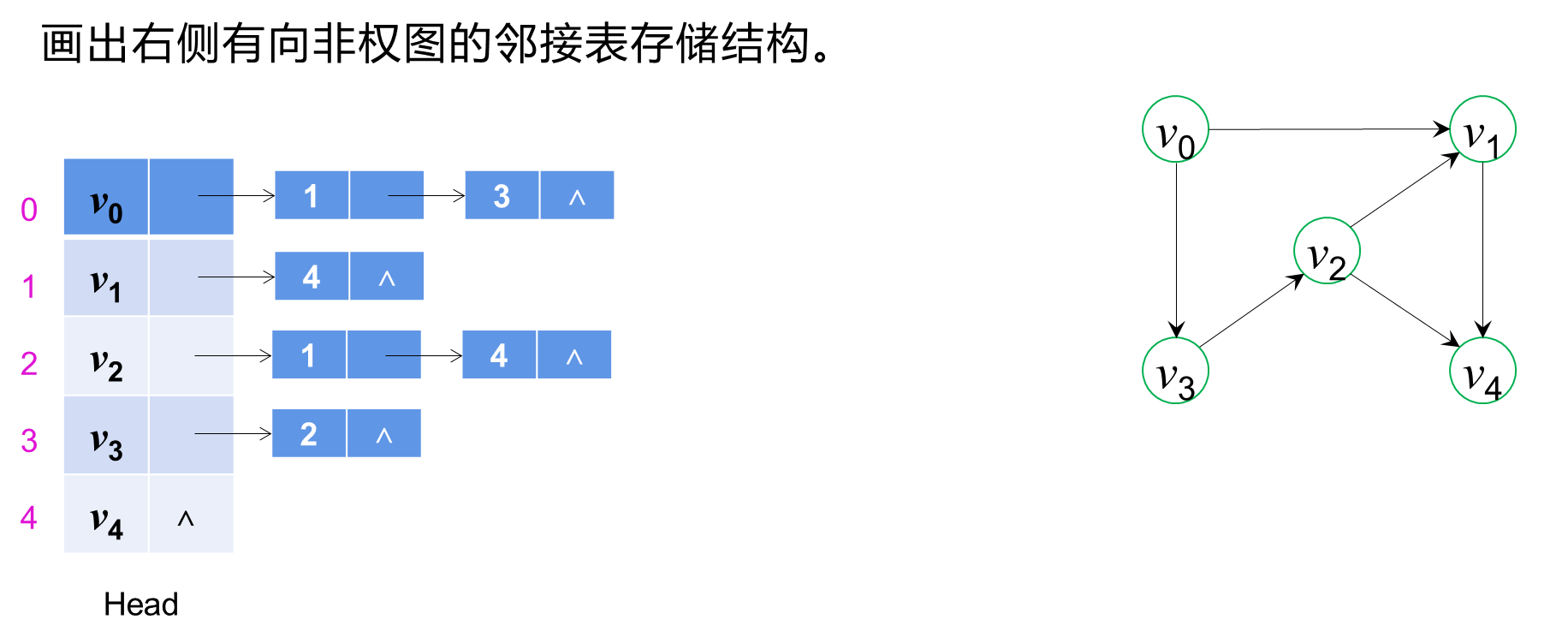
3. 实验内容

3.1 实验题目

  将邻接矩阵存储转换为邻接表存储

（一）数据结构要求

  邻接表中的顶点表用Head 数组存储，顶点表中元素的两个域的名字分别为 VerName和 Adjacent，边结点的两个域的名字分别为 VerAdj 和 link。边链表中的边结点按照顶点序号从小到大的顺序存储。

（二）输入要求

{0,1,1,1,1,0,0},
{0,0,1,1,0,0,0},
{1,0,0,0,0,0,0},
{0,0,1,0,0,0,0},
{0,0,0,0,0,1,1},
{0,0,0,0,0,0,1},
{0,0,0,0,0,0,0}

（三）输出要求

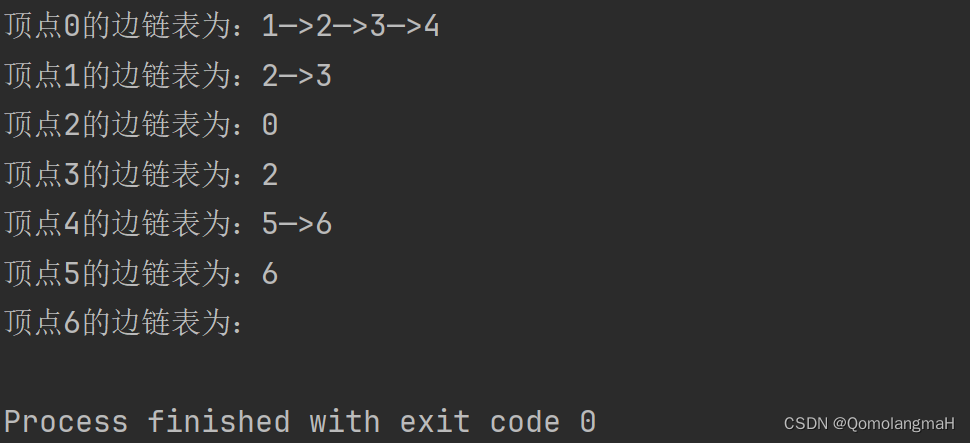
按照顶点编号从小到大的顺序，依次输出每个顶点的边链表。形如：
“顶点 0 的边链表为：1->2->3->4->5->6->7->8”

3.2 算法实现

#include<stdio.h>
#include<stdlib.h>
#define N 7
int A[N][N]={{0,1,1,1,1,0,0},{0,0,1,1,0,0,0},{1,0,0,0,0,0,0},{0,0,1,0,0,0,0},{0,0,0,0,0,1,1},{0,0,0,0,0,0,1},{0,0,0,0,0,0,0}
};
typedef struct P{int VerAdj ;struct P *link;
}P;
typedef struct Q{int VerName;P *Adjacent;
}Q;
typedef struct{Q Head[20];
}Graph;
void Create(Graph *g)
{int i,j,n,t;for(i=0;i<N;i++){g->Head[i].VerName=i;g->Head[i].Adjacent=NULL;P *p=(P*)malloc(sizeof(P));t=0;for(j=0;j<N;j++){if(A[i][j]){if(t==0){//printf("%d&%d ",A[i][j],j);g->Head[i].Adjacent=p;p->VerAdj =j;p->link=NULL;t=1;}else{//printf("%d&%d ",A[i][j],j);P *q=(P*)malloc(sizeof(P));q->VerAdj =j;q->link=NULL;p->link=q;p=q;}}}}
}
void Output(Graph g)
{int i;for(i=0;i<N;i++){printf("顶点%d的边链表为：",i);P *p=g.Head[i].Adjacent;while(p){printf("%d",p->VerAdj );p=p->link;if(p) printf("—>");}printf("\n");}
}
int main()
{Graph g;Create(&g);Output(g);
}

4. 实验结果